シュレーディンガー方程式
シュレーディンガー方程式(シュレーディンガーほうていしき、英: Schrödinger equation)とは、物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者エルヴィン・シュレーディンガーにちなむ。1926年にシュレーディンガーは量子力学の基礎理論に関する一連の論文を提出した[1]。
シュレーディンガー方程式の解は一般的に波動関数と呼ばれる。波動関数はまた状態関数とも呼ばれ、量子系(電子など量子力学で取り扱う対象)の状態を表す。シュレーディンガー方程式は、ある状況の下で量子系が取り得る量子状態を決定し、また系の量子状態が時間的に変化していくかを記述する。あるいは、波動関数を量子系の状態を表すベクトルの成分と見た場合、シュレーディンガー方程式は状態ベクトルの時間発展方程式に置き換えられる。状態ベクトルによる記述は波動関数を用いた場合と異なり物理量の表現によらないため、より一般的である。シュレーディンガー方程式では、波動関数や状態ベクトルによって表される量子系の状態が時間とともに変化するという見方をする。状態が時間変化するという考え方はシュレーディンガー描像と呼ばれる。
分類[編集]
シュレーディンガー方程式はその形式によっていくつかの種類に分類される。
ひとつの分類は時間依存性で、時間に依存するシュレーディンガー方程式と時間に依存しないシュレーディンガー方程式がある。時間に依存するシュレーディンガー方程式(英: time-dependent Schrödinger equation; TDSE)は、波動関数の時間的変化を記述する方程式であり、波動関数の変化の仕方は波動関数にかかるハミルトニアンによって決定される。解析力学におけるハミルトニアンは系のエネルギーに対応する関数だったが、量子力学においてはエネルギー固有状態を決定する作用素[注 1]である。 時間に依存しないシュレーディンガー方程式(英: time-independent Schrödinger equation; TISE)はハミルトニアンの固有値方程式である。時間に依存しないシュレーディンガー方程式は、系のエネルギーが一定に保たれる閉じた系に対する波動関数を決定する。
シュレーディンガー方程式のもう1つの分類として、方程式の線型性がある。通常、線型なシュレーディンガー方程式は単にシュレーディンガー方程式と呼ばれる。線型なシュレーディンガー方程式は斉次方程式であるため、方程式の解となる波動関数の線型結合もまた方程式の解となる。 非線型シュレーディンガー方程式(英: non-linear Schrödinger equation; NLS)は、通常のシュレーディンガー方程式におけるハミルトニアンにあたる部分が波動関数自身に依存する形の方程式である。シュレーディンガー方程式に非線型性が現れるのは例えば、複数の粒子が相互作用する系について、相互作用ポテンシャルを平均場近似することにより一粒子に対するポテンシャルに置き換えることによる。相互作用ポテンシャルが求めるべき波動関数自身に依存する一体ポテンシャルとなる場合、方程式は非線型となる(詳細は例えばハートリー=フォック方程式、グロス=ピタエフスキー方程式などを参照)。本項では主に線型なシュレーディンガー方程式について述べる。
時間に依存するシュレーディンガー方程式[編集]
シュレーディンガー描像では、量子系の時間的変化はその量子系の状態ベクトルや波動関数がその情報を持っていると考える。量子系の状態ベクトルおよび波動関数の時間的変化は、時間に依存するシュレーディンガー方程式によって記述される。状態ベクトル |ψ(t)⟩[注 2]に関するシュレーディンガー方程式は一般に以下のように表される。
ここで i は虚数単位、d/dt は時間に関する微分、 はディラック定数[注 3]である。状態ベクトルの時間微分はヒルベルト空間の元を値に持つ実変数関数の(強)微分として導入される[2]。状態ベクトルの微分とは、以下に示すように、すべての時刻 t において状態ベクトル |ψ(t)⟩ の差分商との差のノルムが 0 に収束するような導関数 d/dt|ψ(t)⟩ のことである。
は系全体の力学的エネルギーを表す演算子で、ハミルトニアン[注 4]と呼ばれる。ハミルトニアンの具体的な中身は考える系に応じて異なり、対応する古典系のハミルトニアンを正準量子化して求めることが多い。
ハミルトニアンは自己共役な演算子であることが要請されるが、ハミルトニアンを自己共役とは限らない一般の線型演算子 に置き換えた方程式
もまたシュレーディンガー方程式と呼ばれる[3]。
シュレーディンガー方程式は非相対論的な方程式であり、相対論的領域に対してそのまま適用することはできない。しかし、ディラック方程式を変形することで相対論的なハミルトニアンを得ることができ、形式的にシュレーディンガー方程式と同様の形に表すことができる[4]。
時間発展[編集]
時間に依存するシュレーディンガー方程式は時間発展演算子を用いて形式的に解を求めることができる。初期条件を
として、各時刻の状態ベクトルを時間発展演算子 (t − t0) を用いて
と書き換える。初期条件を満たすためには時間発展演算子は初期時刻において恒等演算子に等しくなければならない:(0) = I。
時間発展演算子による置き換えをすることにより、シュレーディンガー方程式は時間発展演算子に関する微分方程式となる。
この方程式は以下の積分方程式に置き換えることができる[5]。
積分方程式の右辺を再帰的に展開することにより無限級数として解が求まる。
積分中のハミルトニアンに時間順序演算子 T を作用させ、ハミルトニアンの積を時間順序積に置き換えれば、積分の順序を時間順序演算子に担わせることができる。ハミルトニアンの積の置換は n! 通りあるため、上記の級数は
と書き換えられる。指数関数の級数展開からのアナロジーにより、記述の煩雑さを避けるため時間発展演算子は以下のように略記される。
特にハミルトニアンが時間に依存しない場合、時間発展演算子は単に演算子の指数関数となる。
ハミルトニアンが時間に依存しない例として、ポテンシャル V が時間に依存しない一般の多体系のハミルトニアン
が挙げられる。p は粒子の運動量、x は粒子の位置を表す演算子である。m は粒子の質量であり、それぞれの定数や演算子の添字 k は観測された各粒子を番号付けるものである。また N は系の粒子数を表す。 ハミルトニアンが時間に依存する例としては、量子系が外界と相互作用する場合が挙げられ、特に有名なものとして古典的な電磁場と相互作用する電子のハミルトニアンがある[6]。
ここで A, Φ は電磁ポテンシャルであり、e は電気素量である。
ユニタリ性[編集]
ハミルトニアン の自己共役性と時間発展演算子 の初期条件から、時間発展演算子がユニタリ演算子であることが分かる。時間発展演算子の微分方程式
およびその共役演算子[注 5]に関する微分方程式(ここでハミルトニアンの自己共役性を利用する)
より時間発展演算子とその共役の積は
を満たす。初期条件
より任意の時刻について時間発展演算子はユニタリ性を持つ。
時間発展演算子がユニタリ演算子である場合、状態ベクトルの内積は保存される(つまり、状態ベクトルの内積は時間によらず一定である)。
後述するように状態ベクトルの内積が保存することは、物理的には測定に関する確率の保存則として理解できる。
座標表示[編集]
量子力学において、物理量の固有状態を表す状態ベクトルは完全正規直交系をなすため、任意の状態ベクトルはある物理量の固有状態の線型結合に展開することができる。状態ベクトルを展開した際に各々の固有ベクトルにかかる展開係数を波動関数と呼ぶ。状態ベクトル を位置演算子 の固有ベクトル によって展開すれば、形式的に以下のように表すことができる。
特定の固有ベクトルに対する波動関数は、その双対ベクトル を状態ベクトル にかけることで取り出すことができる。
このことは固有ベクトルの正規性および直交性によっている。
位置演算子の固有ベクトルにかかる波動関数を特に座標表示の波動関数と呼ぶ。シュレーディンガー方程式を座標表示の波動関数によって書き換えれば、
となる[7]。波動関数は位置 x を変数に持つため、時間微分は偏微分に置き換えられる。ここでのハミルトニアンは
として座標表示した波動関数に作用する演算子に置き換えられている。同様に運動量表示の波動関数のシュレーディンガー方程式を考えることもできる。座標表示や運動量表示の波動関数に対するシュレーディンガー方程式は単純な代数方程式ではなく、線型偏微分方程式となる。
物理的意味[編集]
波動関数に物理的な意味が与えられるには、波動関数の空間部分について二乗可積分である必要がある[8]。
可積分性の条件は、波動関数に対して適切な境界条件を課すことで満足される。通常は更に波動関数の規格化条件
を満たすものが非物理的でない解として採用される。
よく知られるように、波動関数の規格化条件は閉じた量子系での大域的な確率保存則と解釈される。確率解釈に基づく通常の量子論では時間発展しても確率が保存されなければならない。つまりどんな場合でもすべての事象の確率の合計は 100% (= 1) にならなければならない。この事とボルンの規則による確率の求め方(状態ベクトルとその双対ベクトルの積から求まる)より、状態ベクトルの時間発展はユニタリ変換でなければならないことが分かる。シュレーディンガー方程式を解くことで、「状態ベクトルの時間発展はユニタリ変換である」ということが導かれる。よって量子系の時間発展についての基本的な要請(原理)は、シュレーディンガー描像で記述する場合は、このシュレーディンガー方程式を採用して出発することが多い。しかし他にも「時間発展演算子が満たすべき条件」を基本的な要請として出発することもある[9]。
波動関数の収縮との関係[編集]

シュレーディンガー方程式を解くと、その系の波動関数がどのように時間発展するかがわかる。
しかしシュレーディンガー方程式は、直接的に波動関数が正確に「何であるか」を語るわけではない。量子力学の解釈は全く別問題であり、「波動関数の根底にある現実と実験結果の間にある関係とは何か」というような問題を扱う。 コペンハーゲン解釈では、波動関数は物理系の完全な情報を与える。
重要な側面は、シュレーディンガー方程式と波動関数の収縮の関係である。 最初期のコペンハーゲン解釈では、粒子は波動関数の収縮の間を「除いて」シュレーディンガー方程式に従い、波動関数の収縮の間は全く異なる動きをする。 量子デコヒーレンスの出現は、別のアプローチ(エヴェレットの多世界解釈のような)を可能にした。それらではシュレーディンガー方程式が常に満たされ、波動関数の収縮はシュレーディンガー方程式から説明される。
代表的な解[編集]
後述する時間に依存しないシュレーディンガー方程式を満たす状態ベクトル |ψ⟩ として、
というものがある。これは時間依存するシュレーディンガー方程式も満たしている。
具体例[編集]

シュレーディンガー方程式の具体的な形は、適当なポテンシャルを決定することで得られる。ポテンシャルは粒子に付随する基本的な変数の関数として与えられる。ただし一般にはポテンシャルの変数は物理量の演算子であり、通常の意味での関数とは異なる。ポテンシャルの変数となる物理量はたとえば粒子の位置であり、スピンである。ポテンシャルは、外界から及ぼされる相互作用と対象とする量子系の粒子間に働く相互作用の二つがある。古典論と同じく一体のポテンシャルは、多体間ポテンシャルを何らかの意味で平均化したものと考えることができる。例えば原子核および内殻電子から外殻電子に及ぼされるクーロン相互作用は、原子核や内殻電子の運動が外殻電子の運動にほとんど影響を受けないならば、原子核と内殻電子に関係するポテンシャルの変数は固定され、二体間ポテンシャルを一体のポテンシャルに置き換えることができる。多体間ポテンシャルの例として最も基本的なものは粒子間のクーロン相互作用およびスピン相互作用である。応用上では有限の井戸型ポテンシャルやレナード-ジョーンズ・ポテンシャルなども利用される。
粒子系のハミルトニアンは前述のポテンシャルの他に、一般には粒子の運動エネルギーが加えられたものになる。具体的なハミルトニアンから波動関数を得るには、物理量の交換関係に従い物理量演算子の表現を決め、得られたハミルトニアンをシュレーディンガー方程式に適用し、その解を求める。
例えば以下の方程式は、位置演算子を掛け算演算子とした場合の一体のポテンシャルに対する一粒子の運動を表す。
一粒子系のシュレーディンガー方程式
m は物体の質量、V(x, t) はポテンシャルエネルギー、∇2 はラプラシアン、ψ(x, t) は位置表示の波動関数である。 ハミルトニアンの中に微分演算子が含まれているため、これは線型偏微分方程式である。これは拡散方程式でもあるが、熱伝導方程式とは違って、時間微分の部分に虚数単位があることによって、波動方程式とも言える。
時間に依存しないシュレーディンガー方程式[編集]
ハミルトニアンが時間に陽に依存しないものとして、時間に依存するシュレーディンガー方程式を時間と空間について変数分離すると、波動関数の空間部分に関する方程式としてハミルトニアンの固有値方程式が得られる。この固有値方程式を時間に依存しないシュレーディンガー方程式と呼ぶ。
時間に依存しないシュレーディンガー方程式
ここで Ψ は波動関数の空間部分、E はエネルギー固有値である。時間に依存しないシュレーディンガー方程式の解はエネルギー固有状態と呼ばれる[10]。
ハミルトニアンのエルミート性から、エネルギー固有状態は互いに直交する。互いに直交する状態間では遷移が起こらないため、固有状態は安定な状態として存在できる。空間部分がハミルトニアンの固有状態であるような波動関数は量子系の定常状態に対応し、定常状態の波動関数とか、単に定常状態とか呼ばれる。あるいは原子や分子に束縛された電子の波動関数に対しては、原子軌道や分子軌道といったように、古典模型の言葉を借用して軌道(英: orbital)と呼ぶこともある。
定常状態の波動関数の時間依存部分は以下のような指数関数で表される。
シュレーディンガー方程式の変数分離解は特別な定常状態の波動関数となるが、解の線型性から一般の波動関数をいくつかの定常状態の線型結合として表すことができる。
ここで Ek は k でラベル付けされたエネルギー固有値、ΨEk は対応する固有状態、cEk はそれぞれの定常状態の確率的な重みを表す複素数である。

具体例[編集]
時間に依存しないシュレーディンガー方程式に対して、磁場のない一粒子系のハミルトニアン
を与えると以下のようになる。
磁場のない一粒子系の場合
上記のハミルトニアンはポテンシャル V(x) を具体的に決めていないが、実際の取り扱いでは、ポテンシャルを具体的な関数として定めたり、何らかの意味で素性の良い関数であることを要求する必要がある。
自由粒子[編集]
何ら相互作用を受けていないような粒子を自由粒子という。自由粒子に対するハミルトニアンにはポテンシャル項がないため (V(x) = 0)、一次元系のシュレーディンガー方程式は以下のようになる[11]。
自由粒子のエネルギー固有値 E は、ハミルトニアンが運動エネルギー演算子に対応するため、粒子が持つ運動エネルギーに対応する。エネルギー固有値の正負によってシュレーディンガー方程式の解の振る舞いは大きく異なる。
エネルギー固有値が正の場合 (E > 0)、自由粒子のシュレーディンガー方程式の解は振動解となる(C1, C2 は任意定数)。
一方、エネルギー固有値が負の場合 (E < 0)、自由粒子のシュレーディンガー方程式の解は指数解となる。
指数解は無限遠での発散などにより、物理的な要請を満たさないため、非物理的な解として扱われる。ただし、トンネル効果のように、部分的に波動関数が指数的な振る舞いをすることは許されている。
自由粒子のシュレーディンガー方程式は、例えば金属中の伝導電子の運動や、無限遠で平坦なポテンシャルを持つ系におけるポテンシャルの束縛を逃れた粒子の振る舞いを調べることなどに応用される。
一定なポテンシャル[編集]

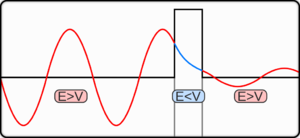
ポテンシャルが一定V = V 0 の場合、シュレーディンガー方程式の解はエネルギーが古典的に許されるかどうかによって異なり、E > V 0 のときは振動解、E < V 0 のとき指数解になる。振動解では粒子は古典的に許されたエネルギーを持ち、解は実際の古典的な運動に対応する。一方で指数解では粒子は古典的に許されないエネルギーを持ち、トンネル効果のため、古典的に許されない領域へも波動関数が滲むことを記述する。ポテンシャルV 0 が無限に大きい場合、運動は古典的な有限の領域に制限される。つまり、全ての解は充分遠方で指数的になる。減少的な指数解によりエネルギー準位は、allowed energies (許容準位)と呼ばれる離散集合に制限する[10]。
調和振動子[編集]

調和振動子のシュレーディンガー方程式は
注目すべきこととして、この量子系は解が厳密に求まり(しかしエルミート多項式のために複雑)、また、振動する原子や分子[12]やまた格子上の原子やイオン[13]、あるいは平衡点近傍で近似したポテンシャルを持つ系など、他の幅広い系を記述し、あるいは近似することができる。このことはまた量子力学における摂動論の基礎を成している。
調和振動子のシュレーディンガー方程式の解は、一般にエルミート多項式を用いて表される。位置表示の波動関数については以下のように与えられる。
ここでn = 0,1,2,... であり、関数Hn はエルミート多項式である。
水素原子[編集]
シュレーディンガー方程式の形式は、水素原子に応用ができる[14][15]。
e は電気素量で、r は電子の位置(r = |r | は位置ベクトルの大きさで、原点からの距離を表す)、ハミルトニアンのポテンシャル項はクーロンの法則を表し、ε0 は真空の誘電率で
は、質量mp の水素原子核(プロトン)と質量me の電子の二体換算質量である。陽子と電子は逆の電荷を持つから、ポテンシャルの項に負符号が現れる。電子質量の代わりに換算質量が使われるのは、電子と陽子が互いに共通の質量中心の周りを運動しているためであり、解くべき問題は二体問題になる。ここでは主に電子の運動に興味があるので、等価な一体問題として、換算質量を使った電子の運動を解くことになる。
水素に対する波動関数は電子の座標の関数で、実際にはそれぞれの座標の関数に分離できる[16]。普通はこれは球面座標系でなされる:
は動径関数で、 は次数 ℓ と位数m の球面調和関数である。水素原子はシュレーディンガー方程式が厳密に解かれる唯一の原子である。多電子原子は近似方法を必要とする。解の仲間は[17]
ここで
ニ電子原子またはイオン[編集]
中性のヘリウム原子(He, Z = 2)や、陰性の水素イオン(H–, Z = 1)、陽性のリチウムイオン(Li+, Z = 3)のような、いかなる二電子系に対する方程式は[18]、
r 1 はひとつの電子の位置(r 1 = |r 1| はその大きさ)で、r 2 はもうひとつの電子の位置(r2 = |r 2| はその大きさ)である。r 12 = |r 12| はそれらの間の距離の大きさであり、r 12 は以下で与えられる。
μ は再び質量M の原子核に対応した電子の二体換算質量であり、ここでは
そして、Z は元素に対する原子番号である(量子数ではない)。
2 つのラプラシアンの交差項
は、mass polarization term として知られ、原子核の運動が原因で現れる。波動関数は 2 つの電子の位置の関数である。
この方程式に対する閉形式解はない。
解法[編集]
|
一般的な方法
|
特殊な場合の方法
|
解の物理的意味[編集]
シュレーディンガー方程式とその解は物理学を飛躍的に進歩させた。シュレーディンガー方程式の解からは当時は予想できなかった結論が得られた。
量子化[編集]
シュレーディンガー方程式は、物理量は量子化される(離散的な値だけが現れる)事があると予測する。例としてエネルギーの量子化があり、原子中の電子のエネルギーは常に離散的になる。これを表したのがエネルギー準位であり、これは原子分光分析で確認されている。また他の例として角運動量の量子化がある。これは初期のボーアの原子模型の時には仮定であったが、シュレーディンガー方程式から導出されるものである。
ただしすべての測定値が量子化されるわけではなく、例えば、位置や運動量、時間やエネルギーは、連続した範囲の値を取り得る。
観測と不確実性[編集]
古典力学では、粒子は常に定まった位置と運動量の組を持つ。これらの値はニュートン力学や一般相対論に従って、決定論的に変化する。しかし量子力学では、粒子は定まった物理量を持たず、観測するたびにある確率分布に従ってランダムに測定結果が決まる。シュレーディンガー方程式はその確率分布を予測するが、本質的に個々の観測の正確な結果を予想することは出来ない。不確定性原理は量子力学が本来的に持つ不確実性の有名な例である。それは、より正確に粒子の位置を確認すると運動量が曖昧になり、その逆も同様となることを主張している。シュレーディンガー方程式は、粒子の波動関数の決定論的な時間発展を説明する。しかし波動関数が厳密に分かったとしても、その波動関数に対して行われる具体的な観測の結果を決める事はできない。
トンネル効果[編集]
古典物理学では、ボールをゆっくりと山の頂上に向けて転がすと、やがてボールは止まり、転がって戻ってくる。これはボールが山の頂上に辿り着き反対側へ行くのに必要なエネルギーを持っていないためである。しかしシュレーディンガー方程式は、ボールが頂上へたどり着くのに十分なエネルギーを持っていなくても、山の反対側へ到達する小さな可能性が存在することを予想している。これがトンネル効果と呼ばれている。これは不確定性原理に関係している。ボールが山のこちら側にいるように見えても、その位置は不確実であり、反対側で確認される可能性がある。
粒子の波動性[編集]

非相対論的なシュレーディンガー方程式は波動方程式とも呼ばれる偏微分方程式の一種である。そのためよく粒子は波として振る舞うのだと言われる。現代の多くの解釈ではこの逆に、量子状態(つまり波)が純粋な物理的実在であり、ある適切な条件の下では粒子としての性質を示すのだとされる。
二重スリット実験は、通常は波が示す、直感的には粒子と関連しない奇妙な振る舞いの例として有名である。ある場所では二つのスリットから来た波同士が打ち消し合い、別の場所では強め合うことで、複雑な干渉縞が現れる。直感的には1個の粒子のみを打ち出した時には、どちらかのスリットのみを通り両方のスリットからの寄与の重ね合わせにならないため、干渉縞は現れないように感じられる。
ところが、シュレーディンガー方程式は波動方程式であるから、一粒子のみを二重スリットに打ち出した時にも同じ干渉縞が「現れる」(左図)。なお、干渉縞が現れるためには実験を繰り返し何度も行う必要がある。このように干渉縞が現れるという事は個々の電子が「両方」のスリットを同時に通る事を示している[19][20][21]。直感と反する事ではあるが、この予言は正しく、この考えで電子回折や中性子回折をよく理解でき、科学や工学で広く使われている。
回折の他に、粒子は重ね合わせや干渉の性質を示す。重ね合わせの性質によって、粒子は古典的には異なる 2 つ以上の状態を同時にとる事ができる。例えば、粒子は同時に複数のエネルギーを持つことや、異なる場所に同時にいる事ができる。二重スリットの実験の例では 2 つのスリットを同時に通ることができるのである。古典的なイメージに反する事ではあるがこの重ね合わせ状態は一つの量子状態のままである。
線型性と平面波[編集]
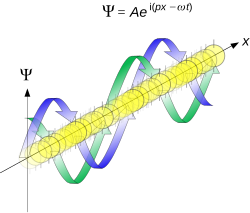
最も単純な波動関数は平面波である:
ここでA は平面波の振幅、k は波数ベクトル、ω は角振動数を表す。一般には、純粋な平面波だけで物理系を記述することはできないが、一般に重ね合わせの原理が成り立つため、すべての波は正弦の平面波の重ね合わせによって作られる。シュレーディンガー方程式が線型なら、平面波の線型結合も解として許される。従って、重ね合わせの原理が成り立つならば、シュレーディンガー方程式は線形微分方程式になる必要がある。
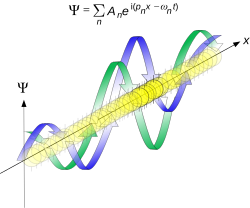
波数k が離散的な場合には、平面波の重ねあわせは単純に複数の波数をもつ平面波の和で表現される:
波数k が連続的な場合には和ではなく積分で表され、波動関数 Ψ(r , t ) は波数空間の波動関数のフーリエ変換となる[10]。
ここでd 3k = dkx dky dkz は波数空間での微小体積であり、積分は波数空間の全体にわたって行われる。運動量波動関数 Φ(k ) が被積分関数として現れているが、これは、位置の波動関数と運動量の波動関数が互いのフーリエ変換であることから生じる。
エネルギー保存則との整合性[編集]
粒子の全エネルギーE は、運動エネルギーT と位置エネルギーV の和である。この和は古典力学では、ハミルトニアンH を表すためにもよく使われる。
明示的に、一次元の粒子について、位置をx 、質量をm 、運動量をp 、位置と時刻t によって変化するポテンシャルエネルギーをV (x , t ) とすると
三次元では、位置ベクトルr と運動量ベクトルp が使われる。
この形式は任意の一定数の粒子の集まりにまで拡大できる。つまり、系の全エネルギーは全ての粒子の運動エネルギーと、系のポテンシャルエネルギーを足しあわせたものであり、またハミルトニアンでもある。しかし、粒子間には相互作用(多体問題)がある可能性があるため、系のポテンシャルエネルギーV は全粒子の空間的な配置の変化と、あるいは時間によって変化する。一般的には系のポテンシャルエネルギーは、それぞれの粒子の持つ位置エネルギーの合計ではなく、粒子のすべての空間位置の関数である。明示的に書くと、
シュレーディンガー方程式の導出[編集]
シュレーディンガー方程式は、その解が波のような動きを表現する関数であるので、数学的には波動方程式と言える。
普通、物理学での波動方程式は他の物理的法則から導かれる。例えば弦や物体の自然振動の波動方程式はニュートンの法則から求められ、そこでは波動関数は物質の変位を表す。電磁波はマクスウェルの方程式から導かれ、そこでは波動関数は電場と磁場を表す。
その一方で、シュレーディンガー方程式の基礎は粒子のエネルギーと、量子力学の仮定である。すなわち、波動関数は系の記述である。シュレーディンガー方程式はそれゆえ、ファインマンが言うように、それ自身の新しい概念である。
| 「 | Where did we get that (equation) from? Nowhere. It is not possible to derive it from anything you know. It came out of the mind of Schrödinger.
(この方程式はどこから導かれたのか? どこからでもない。これを、君が知っているどんなことから導くこともできない。これはシュレーディンガーの頭の中から出てきたのだ。) |
」 |
—Richard Feynman[22] | ||
この方程式は、古典的なエネルギー保存則に立脚する線型微分方程式という構造を持ち、ド・ブロイの関係と整合的である。その解は波動関数 Ψ であり、それは系について知りうる全ての情報を含んでいる。コペンハーゲン解釈では、Ψ の絶対値 |Ψ| は、粒子がある瞬間にある空間配置にいる確率に関係する。方程式を解いて波動関数 Ψ を得れば、具体的なポテンシャルの影響下で粒子が互いに影響し合いながらどのように振る舞うかが予測できる。
シュレーディンガー方程式は原理的には、波動方程式が粒子を記述し得るという、ド・ブロイの仮説を基に成り立ち[14]、後述する方法で構成される[18]。より厳密なシュレーディンガー方程式の数学的導出については例えば [23] を参照。
ド・ブロイの関係との整合性[編集]
アインシュタインの光電効果仮説(1905年)によれば、光子のエネルギーE は、光の対応する光量子波束の周波数 ν(もしくは角周波数 ω = 2πν)に比例する。
同様に、ド・ブロイの仮説(1924年)によれば、どのような粒子も波と関連付けることができ、その粒子の運動量p は、波数ベクトルk に比例する:
特に、1 次元の運動では波数ベクトルk の絶対値は波長 λ に反比例する (k = 2π/λ)。従って、1 次元の運動に限定すれば、上の式は波長 λ を使って以下のように書くこともできる:
プランク-アインシュタインの関係とド・ブロイの関係
は、運動量と空間、時間とエネルギーの間の深い関係を照らしており、波動性と粒子性の二重性を表している。ħ = 1 となるような自然単位系を用いて、方程式 を以下の恒等式 にするとより明白となる。
このような単位系の下では、エネルギーと角振動数は時間の逆数として同じ次元を持ち、運動量と波数は長さの逆数の次元を持つ。したがって、エネルギーと角振動数、運動量と波数は互いに同じものとして入れ替えて使うことができる。自然単位系を用いることによって文字の重複を防ぎ、現れる物理量の次元を減らすことができる。しかしながら自然単位系は馴染みがないため、本稿では以降も国際単位系を用いる。
1925年の終わり、シュレーディンガーの見識は、平面波の位相は以下の関係を使って複素数の力率として表した。
そして空間に対する一次偏微分を
そして時間に対して
導関数を示す
もう一つの量子力学の仮定は、すべてのオブザーバブルは波動関数に作用する自己共役な線型演算子で表され、その演算子の固有値はオブザーバブルの取り得る値になる。前の導関数は、時間微分に対応するエネルギー演算子と
空間微分(ナブラ)に対応する運動量演算子を導く。
ハット (^) は、観測量が演算子であることを示す。演算子は通常の数では表されず、運動量やエネルギーの演算子は微分演算子で表されるが、位置やポテンシャルエネルギーの演算子に関してはただの掛け算演算子になる。面白い点は、エネルギーは時間に関して対称性で、運動量は空間に関して対称性であり、そしてそれらの対称性はエネルギーと運動量の保存則が成り立つ理由である。ネーターの定理を参照。
エネルギー方程式に Ψ を掛け、エネルギー・運動量演算子を置換する。
すぐにシュレーディンガーに彼の方程式を導く。
これらの方程式から、粒子と波の二重性について次のような評価が与えられる。運動エネルギーT は運動量p の二乗に関係する。粒子の運動量が増えれば、運動エネルギーはより早く増加する。しかし波数k が増加するため、波長 λ が減少する。
そして運動エネルギーは二次空間微分に比例するから、波の曲率の強さにも比例する。
曲率が増えるごとに、波の振幅はより速く交互に正負を動き、波長を短くする。運動量と波長の逆比例の関係は粒子の持つエネルギーに整合し、すべての数式で、粒子のエネルギーは波と結び付けられる[14]。
古典力学との関係[編集]
シュレーディンガーが要求したのは以下のようなことである: 位置がr の近くであり, 波数ベクトルがk の近くであるような波束を表す解は, k (従って速度)の広がりがr の広がりを顕著に増やすようなことがないくらいに十分に短い時間内で, 古典力学で決定される曲線を描く。
与えられたk の広がりに対して、速度の広がりはプランク定数に比例するから、プランク定数をゼロに近似したとき、古典力学での方程式は量子力学から導出されると言われる[24]。その極限がどのように取られるか、またどんな状況でかという点で細心の注意が払われる必要がある。
短波長極限はプランク定数をゼロに近似することと等価である。なぜならこれは、波束の局在性を極限まで強め, 粒子を特定の位置に局在化させることだからである(右図を参照)。ハイゼンベルクの不確定性原理を位置と運動量に対して使うと、位置の不確定性と運動量の不確定性の積は、ħ → 0に従ってゼロとなる。
ここでσ は観測量の偏差の二乗平均平方根であり、位置x と運動量px (y とz についても同様)がこの任意の精度で知られるのはこの極限においてでしかない、ということが示唆される。
シュレーディンガー方程式の一般式
と密接に関連している。
ここでS は作用、H は古典力学におけるハミルトニアン関数(演算子ではない)。ハミルトン-ヤコビ方程式で使われる一般化座標系qi (i = 1,2,3) は、r = (q 1, q 2, q 3) = (x, y, z ) としてデカルト座標系の位置に置き換えられる[24]。
代入式
ここで ρ(r , t ) はシュレーディンガー方程式に対する確率振幅である。この波動関数を代入した方程式で極限 ħ → 0を取り、ハミルトン-ヤコビ方程式を導く。
関わりあいは、
- 粒子の動き(シュレーディンガー方程式の(短波長)波束解で説明される)は、動きのハミルトン-ヤコビ方程式により説明される。
- シュレーディンガー方程式は波動関数を含み、そのため波束解は(量子)粒子の位置が、波面にあいまいに広がることを示している。それどころか、ハミルトン-ヤコビ方程式は、定位置定運動量の(古典的)粒子に適用され、その代わり(軌道上の)位置や運動量は決定論的で、同時に知られる。
古典力学と量子力学の時間発展[編集]
古典力学における運動方程式はニュートン力学の運動の第2法則であり、これと等価な式としてオイラー=ラグランジュ方程式や正準方程式(ハミルトン方程式)がある。これらの方程式は、力学系の運動を解き、初期条件や系の配置を指定した時に任意の時間に力学系がどのように振る舞うかを数学的に予測するために使われる。
他方で量子力学では、量子系(通常原子、分子、亜原子粒子のような自由か束縛されているか局在しているもの)のシュレーディンガー方程式が、古典力学における運動方程式に対応し、状態の時間発展を記述する。 ニュートンの運動の第2法則のように、シュレーディンガー方程式はヴェルナー・ハイゼンベルクの行列力学や、リチャード・P・ファインマンの経路積分のような等価な別の表現に書き換えることができる。
相対論とシュレーディンガー方程式[編集]
ニュートンの運動方程式と同じように、シュレーディンガー方程式における時間の扱いは、相対論的な記述にするには不都合である。この問題は行列力学では波動力学ほど深刻ではなく、経路積分の方法では全く問題にならない。
歴史的背景と発展[編集]
マックス・プランクの光の量子化(黒体輻射を参照)にしたがって、アルベルト・アインシュタインは、プランクの量子は光子(光の粒子)であると説明し、光子のエネルギーE はその振動数ν(または角周波数ω)に比例すると提案している(これが波動と粒子の二重性の最初の現れ)。
また、エネルギーと運動量は特殊相対性理論の角周波数と波数と同じ方法で関係しているから、光子の運動量p が波数k と比例関係にあることがわかる。
ルイ・ド・ブロイは、粒子が電子のようなものでも、すべての粒子に対してこの式が正しいと仮説を立てた。 ド・ブロイは、物質波がそれと対応する粒子に伴って伝搬すると仮定すると、電子は定常波を形成する、つまり原子核のまわりで離散的な回転周波数のみが許されることを示した[25]。 これらの量子化された軌道は不連続なエネルギー準位に対応し、ド・ブロイはボーアの原子模型がエネルギー準位を形成することを再現した。ボーアの原子模型は角運動量の量子化の仮定の上で成り立っている。
ド・ブロイによれば、電子は波で表現され、波長の数は電子の軌道の円周上にぴったり収まらねばならない。従って、
このアプローチは本質的に、電子の波を半径r の円周軌道に沿った一次元に限定して考えている。
1921年、ド・ブロイに先立ち、シカゴ大学のアーサー・C・ランが、今で言うド・ブロイの関係を導くために、相対性理論の四元運動量の完成を基にした同様の主張を使った[26]。ド・ブロイと違って、ランはさらに進んで、現在シュレーディンガー方程式と呼ばれるところの微分方程式を定式化し、水素原子のエネルギーの固有値を解いた。不幸にもこの論文はフィジカル・レビューに却下されてしまった。Kamen はこの詳細を述べている[27]。
ド・ブロイの理論が登場すると、物理学者ピーター・デバイは即座に、もし粒子が波として振る舞うなら、それらは何らかの形の波動方程式を満たすべきだと論評した。デバイの見解に刺激を受け、シュレーディンガーは電子の適切な 3 次元波動方程式を見つけようと決意した。シュレーディンガーは、光学と力学を結ぶウィリアム・ローワン・ハミルトンの類推に導かれた。それは、波長を 0 にする極限では光学系は力学系に似るという考え方である(ゼロ波長極限での光の経路は、フェルマーの原理に従った明確な軌跡を描く。光学におけるフェルマーの原理の力学における対応物は最小作用の原理である)[28]。
彼の論証を現代的な表現で以下に記述する。彼の発見した方程式は[29]
しかしそのとき既に、アルノルト・ゾンマーフェルトは相対論補正を使ってボーアの原子模型を改良していた[30][31]。シュレーディンガーは相対性理論のエネルギーと運動量の関係を使って、現在ではクーロンポテンシャルにおけるクライン-ゴルドン方程式として知られるものを見つけようとした:
彼はこの相対論的方程式において定常波を発見したが、相対論補正はゾンマーフェルトの公式と一致しなかった。落胆して彼は計算をやめ、1925年12月、彼は人里離れた山小屋に引きこもってしまった[32]。
山小屋でシュレーディンガーは、初期の非相対論的計算は発表に値する新しさがあると認め、将来にわたって相対論的修正の問題から手を引くことを決めた。水素原子におけるシュレーディンガー方程式の解の難しさ(後に彼は友人の数学者ヘルマン・ワイルに助けられている)にもかかわらず、シュレーディンガーは1926年に発表した論文で、彼の非相対論的な波動方程式は水素の正しいスペクトルのエネルギーを導出することを示している。 その方程式で、シュレーディンガーは水素原子の電子を波 Ψ(x , t ) として扱い、陽子によって作られるポテンシャルの井戸V の中で動くとした上で、水素スペクトル系列を計算した。この計算はボーアの原子模型のエネルギー準位を正確に再現した。論文でシュレーディンガーは自分でこの方程式を以下のように説明している。
| 「 | The already ... mentioned psi-function.... is now the means for predicting probability of measurement results. In it is embodied the momentarily attained sum of theoretically based future expectation, somewhat as laid down in a catalog. | 」 |
この1926年の論文はアインシュタインに熱狂的に支持された。アインシュタインは物質波を自然の直感的な表し方として見ており、ハイゼンベルクの行列力学をあまりに形式的だと非難していた[35]。
シュレーディンガー方程式は波動関数 Ψ の振舞いの詳細を述べるが、その本質について何も述べない。シュレーディンガーは 4 報目の論文で、これを電荷密度として理解しようとしたが、失敗した[36]。1926年、シュレーディンガーの 4 報目かつ最後の論文が発表された数日後、マックス・ボルンは波動関数 Ψ を確率振幅(その絶対値の二乗 |Ψ|2 が確率密度に等しい)として解釈することに成功した[37]。しかしシュレーディンガーは常に統計学的、確率的なアプローチと、それに関連した波動関数の崩壊を反対しており(アインシュタインのように、量子力学はその背後にある決定論に関する統計学的近似であると信じていた)、ついにコペンハーゲン解釈と和解することはなかった[38]。 ド・ブロイは後年、比例係数によって複素関数と対応付けられる実数値波動関数を提唱し、ド・ブロイ=ボーム理論を生み出した。
脚注[編集]
注釈[編集]
- ^ 物理学の文献において作用素は演算子とも呼ばれる。以下では作用素の意味で演算子という語を用いる。
- ^ このようなベクトルの記法をブラ・ケット記法と呼ぶ。 |η⟩ という形のベクトルをケットベクトル、⟨ξ| という形のベクトルをブラベクトルと呼ぶ。文献によっては状態ベクトルに対してブラ・ケット記法が用いられていないが、数学的に意味するところは同じである。
- ^ 誤解のおそれがない限り、単にプランク定数と呼ぶことが多い。
- ^ 古典論におけるハミルトニアンと区別する意味で、あるいは演算子であることを強調する意味で、ハミルトン演算子 (Hamiltonian operator) と呼ぶこともある。
- ^ 物理学の文献において共役演算子は † を用いて示されることが多い。他に標準的な記号として ∗ で示す文献もある。
- ^ ラゲールの陪多項式は文献によって異なった定義がなされる。ラゲールの陪多項式や水素原子を参照。
出典[編集]
- ^ 高林 2010, p. 253, §8.1 定常状態のシュレーディンガー方程式.
- ^ 新井 2003, pp. 454–455, 9.1 強連続 1 パラメータユニタリ群.
- ^ 新井 2003, pp. 467–469, 10.2 量子力学の公理系.
- ^ ランダウ & リフシッツ 2008, pp. 397–398, §83. ディラック行列.
- ^ 以降の時間発展演算子の取り扱いについてはたとえば、(清水 2004, pp. 184–188, 193, 第 6 章 時間発展について) を参照。
- ^ 古典場と電子の相互作用に関する取り扱いについてはたとえば、(江沢 2002, pp. 116–123, 13. 輻射と物質の相互作用) や (ランダウ & リフシッツ 2008, pp. 214–215, 431–437, §43. 磁場のなかの粒子; §92. 外場内の電子に対するディラック方程式) などを参照。(ランダウ & リフシッツ 2008) はシュレーディンガー方程式の相対論的拡張であるディラック方程式や、シュレーディンガー方程式に磁場とスピンの相互作用を含めたパウリ方程式に関しても言及している。
- ^ Shankar 1994, pp. 143ff.
- ^ Feynman, Leighton & Sands 1964, pp. 20–7, volume 3 Operators.
- ^ Sakurai 1989.
- ^ a b c McMahon 2006.
- ^ Shankar 1994, pp. 151ff.
- ^ Atkins 1978.
- ^ Hook & Hall 2010.
- ^ a b c Atkins 1974.
- ^ Atkins 1977.
- ^ a b Tipler & Mosca 2008.
- ^ Griffiths 2008, pp. 162–.
- ^ a b Bransden & Joachain 1983.
- ^ Donati, Missiroli & Pozzi 1973.
- ^ Greene 2003, p. 110.
- ^ Feynman, Leighton & Sands 1965, volume 3.
- ^ Hey & Walters 2009.
- ^ Resnick & Eisberg 1985.
- ^ a b Hand & Finch 2008.
- ^ de Broglie 1925.
- ^ Weissman, Iliev & Gutman 2008.
- ^ Kamen 1985, pp. 29–32.
- ^ Schrödinger 1984, 1926年の第一論文のイントロダクションを参照。.
- ^ Lerner & Trigg 1991.
- ^ Sommerfeld 1919.
- ^ Haar 1967.
- ^ Rhodes 1986.
- ^ Schrödinger 1935, p. 9.
- ^ Wheeler 1983, Section I.11 of Part I.
- ^ Schrödinger et al. 1967.
- ^ Moore 1992, p. 219.
- ^ Moore 1992, p. 220.
- ^ Moore 1992, pp. 220, 479, It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrödinger never accepted the Copenhagen interpretation (cf. p. 220)..
参考文献[編集]
- 高林, 武彦『量子論の発展史』筑摩書房〈ちくま学芸文庫〉、2010年10月10日(原著1977-7-15)。ISBN 978-4-480-09319-6。
- 新井, 朝雄『物理現象の数学的諸原理 ―現代数理物理学入門―』共立出版、2003年2月20日。ISBN 4-320-01726-9。
- ランダウ, レフ、リフシッツ, エフゲニー『量子力学(物理学小教程)』吉村, 滋洋; 井上, 健男(訳)、筑摩書房〈ちくま学芸文庫〉、2008年6月10日(原著1975年4月10日)。ISBN 978-4-480-09150-5。
- 江沢, 洋『量子力学 II』裳華房、2002年4月15日。ISBN 978-4-7853-2207-6。
- 清水, 明『量子論の基礎』(新版)サイエンス社〈新物理学ライブラリ〉、2004年4月25日。ISBN 4-7819-1062-9。
- Sakurai, J.J.『現代の量子力学』 上、桜井明夫訳、吉岡書店〈物理学叢書 56〉、1989年2月。ISBN 978-4-8427-0222-3。
- Shankar, R. (1994). Principles of Quantum Mechanics. Kluwer Academic/Plenum Publishers. ISBN 978-0-306-44790-7
- Resnick, R.; Eisberg, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. ISBN 978-0-471-87373-0
- Feynman, R.P.; Leighton, R.B.; Sands, M. (1964). The Feynman Lectures on Physics. 3. Addison-Wesley. ISBN 0-201-02115-3
- Feynman, R.P.; Leighton, R.B.; Sands, M. (1965). Feynman Lectures on Physics. 3. Addison-Wesley. ISBN 0-201-02118-8
- McMahon, D. (2006). Quantum Mechanics Demystified. USA: McGraw Hill. ISBN 0-07-145546-9
- Atkins, P.W. (1978). Physical Chemistry. Oxford University Press. ISBN 0-19-855148-7
- Atkins, P.W. (1974). Quanta: A handbook of concepts. Oxford University Press. ISBN 0-19-855493-1
- Atkins, P.W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. 1. Oxford University Press. ISBN 0-19-855129-0
- Hook, J.R.; Hall, H.E. (2010). Solid State Physics. Manchester Physics Series (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92804-1
- Tipler, P.A.; Mosca, G. (2008). Physics for Scientists and Engineers — with Modern Physics (6th ed.). W. H. Freeman. ISBN 0-7167-8964-7
- Griffiths, David (2008). Introduction to elementary particles. Wiley-VCH. ISBN 978-3-527-40601-2 2011年6月27日閲覧。
- Donati, O.; Missiroli, G. P.; Pozzi, G. (1973). “An Experiment on Electron Interference”. American Journal of Physics 41 (5): 639–644. doi:10.1119/1.1987321.
- Greene, Brian (2003-10-17). The Elegant Universe. W. W. Norton. ISBN 978-0393058581
- Hey, T.; Walters, P. (2009). The New Quantum Universe. Cambridge University Press. ISBN 978-0-521-56457-1
- Bransden, B.H.; Joachain, C.J. (1983-09). Physics of Atoms and Molecules. Longman. ISBN 0-582-44401-2
- Hand, L.N.; Finch, J.D. (2008). Analytical Mechanics. Cambridge University Press. ISBN 978-0-521-57572-0
- de Broglie, L. (1925). “Recherches sur la théorie des quanta [On the Theory of Quanta]”. Annales de Physique 10 (3): 22–128. 英訳.
- Weissman, M.B.; Iliev, V. V.; Gutman, I. (2008). “A pioneer remembered: biographical notes about Arthur Constant Lunn”. Communications in Mathematical and in Computer Chemistry 59 (3): 687–708.
- Kamen, Martin D. (1985). Radiant Science, Dark Politics. Berkeley and Los Angeles, CA: University of California Press. ISBN 0-520-04929-2
- Schrödinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 3-7001-0573-8
- Lerner, R.G.; Trigg, G.L. (1991). Encyclopaedia of Physics (2nd ed.). VHC publishers. ISBN 0-89573-752-3
- Sommerfeld, A. (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7
- Haar, T. (1967). The Old Quantum Theory. Pergamon Press. ISBN 978-0080121024.
- Rhodes, R. (1986). Making of the Atomic Bomb. Touchstone. ISBN 0-671-44133-7
- Schrödinger, Erwin (1935). Trimmer, John D. (trans.). “The Present situation in Quantum Mechanics”. Proceedings of the American Philosophical Society 124: 323-38.
- Wheeler, J.A. (1983). Zurek, W.H.. ed. Quantum Theory and Measurement. New Jersey: Princeton University Press
- Schrödinger, E.; Planck, M.; Einstein, A.; Lorentz, H.A. (1967). Letters on Wave Mechanics: Schrodinger-Planck-Einstein-Lorentz. Przibram, K. (Editor) (1st ed.). Philosophical Library
- Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. ISBN 0-521-43767-9































![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\psi ({\boldsymbol {x}},t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V({\boldsymbol {x}},t)\right]\psi ({\boldsymbol {x}},t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e05f9d61e955959a07d2ec6cbf3266601a7b7f)















![{\displaystyle \psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aaf51710a4718d8bd8bd8ddb947836b6bd0f30e)



![{\displaystyle E\psi =-\hbar ^{2}\left[{\frac {1}{2\mu }}\left(\nabla _{1}^{2}+\nabla _{2}^{2}\right)+{\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\right]\psi +{\frac {e^{2}}{4\pi \epsilon _{0}}}\left[{\frac {1}{r_{12}}}-Z\left({\frac {1}{r_{1}}}+{\frac {1}{r_{2}}}\right)\right]\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c8d25001a4a294e7d0e0f2daa1fe0edcf56f34f)