光子
| 光子 | |
|---|---|
 | |
| 組成 | 素粒子 |
| グループ | ゲージ粒子 |
| 相互作用 | 電磁力 |
| 理論化 | アルベルト・アインシュタイン |
| 記号 | γ, hν または ħω |
| 質量 |
0 <1×10−18 eV/c2[1] |
| 平均寿命 | Stable[1] |
| 電荷 |
0 <1×10−35 e[1] |
| スピン | 1 |
| パリティ | −1[1] |
| Cパリティ | −1[1] |
| 凝縮対称性 | I(JPC)=0,1(1−−)[1] |
概要[編集]
古代から、光の本性については「光の波動説」と「光の粒子説」の2つが存在し、長い間にわたって対立していた。19世紀末ごろに電磁場に対するマックスウェルの理論がハインリヒ・ヘルツによって検証され、光の波動説は確立された。しかし、光の波動性は黒体放射のエネルギー分布を説明することができなかった。そのため、マックス・プランクは物質のエネルギー吸収・放出の性質としてエネルギー量子の概念を発表した。
ドイツの物理学者のアルベルト・アインシュタインは、光の波動説を支持しつつ、新しい光の粒子説(光量子仮説)を主張した[2]。
アメリカの物理化学者ギルバート・ニュートン・ルイスは古典的な光の粒子説を採用した上で、アインシュタインと同種の領域で内容的に異なる具体的な研究成果を上記研究に1年遅れて発表した。
それぞれ微妙に異なる光の本性に関する研究が平行していたが、第一次世界大戦を経た1920年代に入ると、アーサー・コンプトンによるコンプトン効果の研究に端を発して、1926年から1927年頃にかけて、それら二つの系統は光子(photon)という名称で一応の統一がなされた[注 3][注 4]。
量子論では光子は「ボース粒子」と呼ばれる分類の量子である。
物理的性質[編集]
マイケルソン・モーリーの実験によれば、真空中の光速は c である。電磁波の放射圧は、単位時間単位面積当たりの光子の運動量の転移に由来する[3]。
光子は常に真空中の光の速度と同じ速度で動く。
光線中の振動数 ν の光子に対して、以下のようにエネルギー ε と運動量 p を定義することができる。これは、外部光電効果とコンプトン効果の実験結果により確認されている。
またルイスによれば、光子の静止質量 mrestは0である。
- 素粒子論における物理的性質
光子は電荷を持たない[4]。質量はゼロであり、寿命は無い。光子は2次元の偏光状態を持つ。波数ベクトルの成分は、波長λとその伝播方向を決定する。光子は電磁気のゲージ粒子であり[5]、そのため光子のその他の量子数(レプトン数、バリオン数、フレーバー量子数)はゼロである[6]。
光子は様々な自然過程で放出される。例えば、あらゆる物体は熱放射により、常に光子を放出し続けている。また、電荷が加速されるとシンクロトロン放射を発する。分子、原子、原子核が低いエネルギー準位に遷移すると、赤外線からガンマ線まで様々なエネルギーの光子が放出される。粒子とその反粒子が対消滅する時にも光子が発生する(例えば電子-陽電子対消滅)。
光子は、周波数とは独立なスピン角運動量も運ぶ[7]。スピンの大きさはで、運動の方向に沿って測定される成分であるヘリシティーは±ħである。二つのヘリシティーの値は右巻き、左巻きと呼ばれ、光子の2つの円偏光の状態に対応する[8]。
空間で粒子と反粒子が対消滅すると、少なくとも二つの光子が生成される[注 5]。別の見方をした場合、光子は自身の反粒子と考えることもできる。逆過程の対生成は、ガンマ線等の高エネルギーの光子が物質の中を進む間にエネルギーを失う過程である[9]。この過程は、原子核の電磁場で「一つの光子を生み出す対消滅」の逆過程である。
光子の質量に関する仮説[編集]
光子は、現在では厳密に質量ゼロと理解されているが、ごくわずかな質量をもつ可能性は残されている。もし光子の質量が厳密にゼロでなければ、光の速さは光速cよりも少しだけ遅くなるはずである。この場合、光速cは、全ての物体が理論的に超えられない最高速度ということになるが、相対性理論は影響されない[10]。
光子に質量があると仮定すると、クーロンの法則が修正され、電磁場は余分な物理学的自由度を持つことになる。クーロンの法則が完全な真でなければ、外部電磁場に晒される中空導体の内部に電磁場が発生することになる[11]。ただし、クーロンの法則は非常に高い確度を持つことが確認されており、もし光子に質量があるとしても、その上限は m ≲ 10−14 eV/c2の範囲である[12]。
銀河の磁位ベクトルの効果を検出することで、さらに精度の良い上限値を得ることができる。銀河の磁場は非常に遠くまで届くため、その磁位ベクトルは巨大であるが、光子の質量がゼロであれば磁場のみが観測される。もし光子が質量を持てば、質量項は銀河のプラズマに影響を与えるはずである。そのような効果は検出されていないことから、光子の質量の上限はm < 3×10−27 eV/c2と示唆される[13]。銀河の磁位ベクトルは、帯磁環のトルクを測定することで直接検出することが可能である[14]。そのような方法を用いて、パーティクルデータグループにより10−18 eV/c2(原子質量単位の1.07×10-27倍に相当)という上限値が得られた[15]。
銀河の磁位ベクトルを用いた質量上限の推定は、モデルに依存することが示されている[16]。光子の質量がヒッグス機構によって生み出される場合は、クーロンの法則が正当化され、上限値はm ≲ 10−14 eV/c2となる。
超伝導体中の光子は、ゼロではない有効質量を持ち、その結果、電磁力の届く範囲は超伝導体中の短い範囲になる[17]。
歴史的発展[編集]

古代・中世を通して光は哲学者や自然を研究する学者にとって関心の的であった。光の本性についての研究は、大きく「光の波動説」と「光の粒子説」の二つが存在しておりそれぞれ歴史的に対立をしていた。
ニュートン力学を完成させたアイザック・ニュートンなどは粒子説に基づくモデルを提案していたことから、18世紀までは光の粒子説が優勢に立っていた。ところが、19世紀初頭、トーマス・ヤングとオーギュスタン・ジャン・フレネルが光の干渉と回折を明確に示したことから、19世紀中頃には光の波動説が優勢に立つこととなった[18]。さらに、1865年には、ジェームズ・クラーク・マクスウェルは光は電磁波の一種であると予測し、それを1888年にハインリヒ・ヘルツが実験的に確かめたことから、光の本性としての光の波動説は確定されたかのようにみなされた。
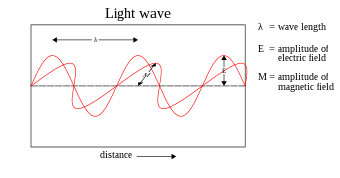
ところが、19世紀末ごろになると、黒体輻射のエネルギー分布式を理論的に求めるにあたって、光の波動説を代表するマックスウェル方程式などでは説明しきれないことが問題となり始めた。
1900年、マックス・プランクは黒体輻射のエネルギー分布式の問題点[19]を解決するにあたって、物質が放出または吸収するエネルギーは連続量とするのではなく振動数 ν に比例した有限の大きさ E =hν をもつ塊と考えるとうまく実験結果と合うと発表し[20][21]、この最小エネルギー単位をエネルギー要素(energy element)と呼んだ[20]。これはあくまで光の波動説に立ったもので、あくまで物質的な制約だと考えられた。
1905年、アルベルト・アインシュタインは、電磁波が広がる際のエネルギー配分は空間的に連続的に行われないと主張し[注 6]、そのエネルギー量子の大きさはその振動数に比例すると仮定すると[注 7]、(外部)光電効果[注 8]などをうまく説明することができることを示した[22][23]。アインシュタインはこれを光量子(light quantum)と呼び[注 9]、さらにプランクが導入した仮説を光量子仮説と名付けた[24]。
- (h : プランク定数、 ν : 光の振動数、 ε : 振動数 ν の光の中の光量子のエネルギー)
1908年、アメリカの物理化学者のギルバート・ニュートン・ルイスは、アインシュタインの1905年に発表した特殊相対性理論の論文を参照してはいるものの特殊相対性原理を無視して、代わりに光量子仮説とも異なる完全な光の粒子説(光の粒子が光速で運動するとき、エネルギー、質量そして運動量をもつ)を前提とし、物体の質量はその速度に依存するという公理を持つ非ニュートン力学の体系を発表した(ルイスの非ニュートン力学)[25][26]。この体系によれば、静止質量(rest mass)と呼ばれる質量概念を定義した上で、光の粒子はもし光速よりもわずかに遅くなったとするとその質量は0になると結論した[注 10]。
- (mrest : 光の粒子の静止質量)
1909年、アインシュタインは光の波動説の前提であるエーテル概念を放棄の上、光の波動説と光の粒子説を融合させることが必要であると主張した[27]。
1916年、アインシュタインは輻射による吸収や放出の際には運動量の付与も起こると述べ[28]、光量子仮説に実質的な変更が加えられた(光量子仮説はエネルギーに関するもので、1909年の論文でわずかに触れてはいたものの[27]、運動量については何も述べていなかった)。
1918年頃から現在コンプトン効果と呼ばれる現象に、古典的な理論で説明を与えることに取り組んでいたアーサー・コンプトンは、1922年に至って古典的理論ではこの現象は説明できないと結論し、光量子仮説とルイスらの理論を組み合わせるようにX線はエネルギー hν、運動量 hν/c をもつ粒子とみなした上で、「光の粒子と自由電子が弾性衝突する」というモデルでコンプトン効果を説明し、このときのアインシュタインの光量子仮説の正当性を立証する形で1923年春に最終的な報告を提出した[注 11][29][30]。この影響を受けるような形で、1922年11月に、光電効果の法則の発見によって、変則的に一年遡って1921年分のノーベル物理学賞がアインシュタインに与えられることが決定した[31][32]。
- (ν : 光の振動数、 p : 振動数 ν の光の中の光量子の運動量)
1926年、もともと光の粒子は運動量を持つということを主張していたギルバート・ルイスは、ギリシア語で「光」を意味するφῶςを由来にこの光の粒子をphoton(フォトン、光子)と名付けた[33][注 12]。翌1927年10月には、コンプトンの提案[34]で開催された第5回ソルベー会議では主題が"Electrons et photons (電子と光子)"と、早速 "photon" の用語が取り入れられることとなった[注 13]。同年1927年にはアーサー・コンプトンがコンプトン効果の研究でノーベル物理学賞を受賞すると、多くの科学者が光の量子化の正当性を受け入れ、光量子を表すルイスのphotonという用語を受け入れた。
量子論では、光子はボース粒子であり、標準模型ではさらにゲージ粒子に分類されている。電荷、質量、スピン角運動量等の光子に固有の性質はゲージ理論から決定される。光子の概念は、レーザー、ボーズ・アインシュタイン凝縮、量子場理論、量子力学の確率振幅等、実験物理学及び理論物理学に重大な進歩をもたらし、光化学、2光子励起顕微鏡、蛍光共鳴エネルギー移動等といった応用がある。また、光コンピューティングや、量子コンピュータの提案のうちのいくつかは光子を利用する。
湯川秀樹は、この電磁気力の媒介粒子としての光子のモデルを根拠に、原子の安定性をもたらす原子核を構成する力(核力)の媒介粒子として中間子と呼ばれる粒子が存在する、という理論を1935年(昭和10年)に提出した(中間子論)[35][注 14]。これは現代の素粒子論の契機となった。
その他全ての素粒子と同様に、現在のところ光子は量子力学で最も良く説明され、粒子と波動の二重性を示す。例えば、一つの光子はレンズで屈折し、また自身と干渉するが、位置が明確に測定できる等、粒子としての振舞い[36]も見せる。
初期の反対論[編集]
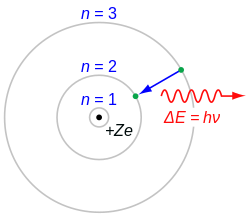
アインシュタインの1905年の予測は、ロバート・ミリカンのノーベル・レクチャーでも詳しく語られたように、20世紀の最初の20年間で様々な実験によって実証された[37]。しかし、1922年にコンプトンの実験で[29]光子が波数に比例した角運動量を運ぶことが示されるまでは、ほとんどの物理学者は電磁放射自体が粒子であることを信じられなかった(例えば、ヴィルヘルム・ヴィーン[19]、マックス・プランク[21]、ミリカン[37]のノーベルレクチャー)。その代わり、エネルギーの量子化は物質の未知の制約に由来するという考えが広く信じられた。しかし、量子化を光自身に帰さなければ解釈の難しいコンプトン効果の実験等で、徐々に態度が変わっていった[38]。
コンプトンの実験の後でも、ニールス・ボーア、ヘンリク・アンソニー・クラマース、ジョン・クラーク・スレイターらは、マクスウェルの連続電磁場モデル、いわゆるBKSモデルを最後まで守り続けた[39]。当時得られていたデータを説明するため、2つの過激な仮説が作り出された。
- エネルギーと運動量は、物質と放射の相互作用で平均でしか保存されず、吸収や放出のような本質的な過程では保存されない。
- 因果律を放棄する。
しかし、改良されたコンプトン効果の実験で、エネルギー-運動量は非常に良く保存されることが示され、またコンプトン散乱における電子の振動と新しい光子の生成は、10ピコ秒以内で因果律に従った。その結果、ボーアらは彼らのモデルに「できるだけ立派な葬式」を挙げることにした[40]。BKSモデルは頓挫したものの、ヴェルナー・ハイゼンベルクに行列力学の着想を与えることとなった[41]。
それでも少数の物理学者は、電磁放射を量子化せず、物質のみが量子力学の法則に従うという半古典的モデルを発展させることに固執した[42]。1970年代には化学実験や物理実験から光子の存在の証拠が圧倒的になるものの、光と物質の相互作用に依っていたために、完全に決定的なものとは見なされなかった。1970年代から1980年代には、全ての半古典的理論が決定的に否定され、量子化は光自体の性質だとするアインシュタインの仮説は証明されたとみなされた。
関連項目[編集]
- 光
- 光学 - 分光学
- ボーアの相補性原理 - ハイゼンベルクの不確定性原理 - 素粒子物理学
- ソリトン
- ソルベー会議
- アルベルト・アインシュタイン
- ギルバート・ルイス
- ルイス=トルマンの非ニュートン力学
脚注[編集]
注釈[編集]
- ^ この記号はおそらくガンマ線に由来する。なお、化学や光工学では、光子は通常hνの記号で光子のエネルギーとして表される。ここで、hはプランク定数、νは周波数である。また稀に周波数をfとしてhfで表されることもある。
- ^ 波動の側面を強調する場合、現代でも光量子の用語を使うことがある。水島(1994) pp.32-33
- ^ 2人の研究成果は互いに補うものようなものであり、光の本性の研究に対する貢献の大きさとしてはどちらに帰属するかどうかは確定が難しいものである。
- ^ なお、アインシュタインの残りの人生の大半を占めた統一場理論の探求の目的は、如何にしてマクスウェルの波の理論と実験で観測される粒子としての性質を統合するかであったと言われる。Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 0-19-853907-X
- ^ なぜならば、基準系の重心では、衝突した反粒子は正味の運動量を持たないのに対して単一の光子は(周波数や波長がゼロにはならないため)常に運動量を持つ。そのため、運動量保存則を満たすために、正味の運動量がゼロとなる少なくとも二つの光子が生成される必要がある(ただし、陽電子が原子核中の陽子と対消滅する場合等、系が別の粒子や場と相互作用している場合は、クーロン力が並進対称性を破るため、一つの光子が生成することが可能である)。二つの光子のエネルギー(周波数)は、運動量保存則で決定される。
- ^ マクスウェル方程式は電磁波の可能なすべてのエネルギーを対象とするものであったので、ほとんどの物理学者は当初、プランクのエネルギーの量子化は、放射を吸収、放出する物質の未知の制約に由来すると考えていた。しかし、アインシュタインはこのとき初めて、エネルギーの量子化は電磁放射自体の性質として提案した。
- ^ 特に光子モデルでは光のエネルギーは周波数に依存するとし、物質と放射としての振舞いを熱平衡で説明する。また、マックス・プランクが半古典モデルで説明しようとした黒体放射の性質も説明できる。半古典モデルは量子力学の発展に貢献した。Kimble, H.J.; Dagenais, M.; Mandel, L. (1977). “Photon Anti-bunching in Resonance Fluorescence”. Physical Review Letters 39 (11): 691-695. Bibcode: 1977PhRvL..39..691K. doi:10.1103/PhysRevLett.39.691.
- ^ 光電効果は、1887年にヘルツ及び翌1888年にドイツの物理学者ヴィルヘルム・ハルヴァックス(Wilhelm Hallwachs)によって発見された 。
- ^ quanta(量子)という用語は1900年以前から、電気を含む離散量を表す用語として使われていたことから、これは次第にエネルギー量子(energy quantum)と呼ばれるようになっていた。
- ^ 他にもアインシュタインが近似式としてしか得ていなかった公式 E=mc2 を精確な結果として導出することができた。
- ^
なお、"輻射の量子がエネルギーとともに方向をもった運動量を運ぶことをきわめて説得的に示す"というコンプトンの結論に対して、当初は強い反対があったが、1924年には完全に受け入れられるようになったということである。
物理学史II(1968) pp.183-184 - ^ ただし、ルイスの光の粒子の概念は生成も破壊もされない光の原子に相当するもので、アインシュタインの光量子概念とは異なっていた。
- ^ この定式化されたばかりの量子力学が議論されたこの第5回はソルベー会議全体の中でももっとも有名な会議である。しかしながら、主題にあげられた光子(photon)の命名を前年に行ったばかりのルイス自身は会議に招待されなかった。代わりにルイス=ラングミュアの原理で知られるアメリカの物理化学者のアーヴィング・ラングミュアが、主題の量子力学への貢献は何もないのになぜか招待された。
Coffey(2008) p.188 - ^ 現代物理学において、原子に対してどのような操作を加えても変化せず安定的である根拠は、この湯川の中間子論に求められる。
出典[編集]
- ^ a b c d e f Amsler, C. et al. (Particle Data Group) (2008 +2009 partial update). “Review of Particle Physics: Gauge and Higgs bosons”. Physics Letters B 667: 1. Bibcode: 2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018.
- ^ C・ロヴェッリ『すごい物理学講義』河出文庫、2019年、148頁。
- ^ E.g., Appendix XXXII in Born, M. (1962). Atomic Physics. Blackie & Son. ISBN 0-486-65984-4
- ^ Kobychev, V.V.; Popov, S.B. (2005). “Constraints on the photon charge from observations of extragalactic sources”. Astronomy Letters 31 (3): 147-151. arXiv:hep-ph/0411398. Bibcode: 2005AstL...31..147K. doi:10.1134/1.1883345.
- ^ Role as gauge boson and polarization section 5.1 inAitchison, I.J.R.; Hey, A.J.G. (1993). Gauge Theories in Particle Physics. IOP Publishing. doi:10.1201/9781315275253. ISBN 0-85274-328-9
- ^ See p.31 inAmsler, C.; et al. (2008). “Review of Particle Physics”. Physics Letters B 667: 1-1340. Bibcode: 2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018.
- ^ Raman, Chandrasekhara Venkata; Bhagavantam, S (1931) (PDF). IJP V6 p353.pdf Experimental proof of the spin of the photon. Indian Association for the Cultivation of Science.
- ^ E.g., section 1.3.3.2 in Burgess, C.; Moore, G. (2007). The Standard Model. A Primer. Cambridge University Press. ISBN 0-521-86036-9
- ^ E.g., section 9.3 in Alonso, M.; Finn, E.J. (1968). Fundamental University Physics Volume III: Quantum and Statistical Physics. Addison-Wesley
- ^ Mermin, David (February 1984). “Relativity without light”. American Journal of Physics 52 (2): 119-124. Bibcode: 1984AmJPh..52..119M. doi:10.1119/1.13917.
- ^ Plimpton, S.; Lawton, W. (1936). “A Very Accurate Test of Coulomb's Law of Force Between Charges”. Physical Review 50 (11): 1066. Bibcode: 1936PhRv...50.1066P. doi:10.1103/PhysRev.50.1066.
- ^ Williams, E.; Faller, J.; Hill, H. (1971). “New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass”. Physical Review Letters 26 (12): 721. Bibcode: 1971PhRvL..26..721W. doi:10.1103/PhysRevLett.26.721.
- ^ Chibisov, G V (1976). “Astrophysical upper limits on the photon rest mass”. Soviet Physics Uspekhi 19 (7): 624. Bibcode: 1976SvPhU..19..624C. doi:10.1070/PU1976v019n07ABEH005277.
- ^ Lakes, Roderic (1998). “Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential”. Physical Review Letters 80 (9): 1826. Bibcode: 1998PhRvL..80.1826L. doi:10.1103/PhysRevLett.80.1826.
- ^ Amsler, C; Doser, M; Antonelli, M; Asner, D; Babu, K; Baer, H; Band, H; Barnett, R et al. (2008). “Review of Particle Physics?”. Physics Letters B 667: 1. Bibcode: 2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018. Summary Table
- ^ Adelberger, Eric; Dvali, Gia; Gruzinov, Andrei (2007). “Photon-Mass Bound Destroyed by Vortices”. Physical Review Letters 98 (1): 010402. arXiv:hep-ph/0306245. Bibcode: 2007PhRvL..98a0402A. doi:10.1103/PhysRevLett.98.010402. PMID 17358459. preprint
- ^ Wilczek, Frank (2010). The Lightness of Being: Mass, Ether, and the Unification of Forces. Basic Books. p. 212. ISBN 9780465018956
- ^ Buchwald, J.Z. (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. University of Chicago Press. ISBN 0-226-07886-8. OCLC 18069573
- ^ a b Wien, W. (1911年). “Wilhelm Wien Nobel Lecture”. 2012年12月8日閲覧。
- ^ a b Planck, M. (1901). “On the Law of Distribution of Energy in the Normal Spectrum”. Annalen der Physik 4 (3): 553-563. Bibcode: 1901AnP...309..553P. doi:10.1002/andp.19013090310. オリジナルの2008年4月18日時点におけるアーカイブ。.
- ^ a b Planck, M. (1920年). “Max Planck's Nobel Lecture”. 2012年12月8日閲覧。
- ^ Einstein, A. (1905). “Uber einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”. Annalen der Physik 17 (6): 132-148. Bibcode: 1905AnP...322..132E. doi:10.1002/andp.19053220607.(光の発生と変脱とに関するひとつの発見的方法について) 光量子論(1969)収録
- ^ Grangier, P.; Roger, G.; Aspect, A. (1986). “Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences”. Europhysics Letters 1 (4): 173-179. Bibcode: 1986EL......1..173G. doi:10.1209/0295-5075/1/4/004.
- ^ A.Einstein (1906), Zur Theorie der Lichterzeugung und Lichtabsorption, 20, pp. 199-206(光の発生と光の吸収の理論について)光量子論(1969)収録
- ^ Gilbert N. Lewis (1908), “A Revision of the Fundamental Laws of Matter and Energy”, Philosophical Magazine, 6th series: 510-523(物質とエネルギーに関する基本法則の一修正) 相対論(1969) 収録
- ^ Gilbert N. Lewis (1908). “LIX. A revision of the fundamental laws of matter and energy”. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Taylor & Francis) 16 (95): 705-717. doi:10.1080/14786441108636549.
- ^ a b Einstein, A. (1909). “Uber die Entwicklung unserer Anschauungen uber das Wesen und die Konstitution der Strahlung”. Physikalische Zeitschrift 10: 817-825.光量子論(1969)収録
- ^ Einstein, A. (1916). “Zur Quantentheorie der Strahlung”. Mitteilungen der Physikalischen Gesellschaft zu Zurich 16: 47. Also Physikalische Zeitschrift, 18, 121-128 (1917). (輻射の量子論) 光量子論(1969)収録
- ^ a b Compton, A. (1923). “A Quantum Theory of the Scattering of X-rays by Light Elements”. Physical Review 21 (5): 483-502. Bibcode: 1923PhRv...21..483C. doi:10.1103/PhysRev.21.483.
- ^ アイザック・アシモフは、アーサー・コンプトンが1923年に光子としてのエネルギーの量子化を定義したと記している。Asimov, I. (1966). The Neutrino, Ghost Particle of the Atom. Garden City (NY): Doubleday. ISBN 0-380-00483-6. LCCN 66-3、Asimov, I. (1966). The Universe From Flat Earth To Quasar. New York (NY): Walker. ISBN 0-8027-0316-X. LCCN 66-5
- ^
C・ゼーリッヒ 著、広重 徹(訳) 編『アインシュタインの生涯』1974年。 p.152 の訳注
なお、アインシュタインはこの決定を、たまたま旅行中の船の上で聞いたと言われる。 - ^ Presentation speech by Svante Arrhenius for the 1921 Nobel Prize in Physics, December 10, 1922. Online text from [nobelprize.org], The Nobel Foundation 2008. Access date 2008-12-05.
- ^ Lewis, G.N. (1926). “The conservation of photons”. Nature 118 (2981): 874-875. Bibcode: 1926Natur.118..874L. doi:10.1038/118874a0., The origin of the word "photon"
- ^ :"At Compton's suggestion, the Fifth Solvey Conference on Physics in 1927 adopted Lewis's term "photon" for the particle that carried radiation, but as used it did not signify Lewis's atom of radiation but rather Einstein's quantum."
Coffey(2008) pp.182-183から引用。なおコンプトン兄弟(アーサー・コンプトン、カール・コンプトン)の内どちらの提案であるかは記載がない。 - ^ 中村誠太郎『湯川秀樹と朝永振一郎』読売新聞社、1992年。 p.28、 田中正『湯川秀樹とアインシュタイン』岩波書店、2008年。 p.103
- ^ この直接的証拠とされる写真とその考え方については、有馬(1994) p.2,4 参照。
- ^ a b Millikan, R.A (1924年). “Robert A. Millikan's Nobel Lecture”. 2012年12月8日閲覧。
- ^ Hendry, J. (1980). “The development of attitudes to the wave-particle duality of light and quantum theory, 1900-1920”. Annals of Science 37 (1): 59-79. doi:10.1080/00033798000200121.
- ^ Bohr, N.; Hendrik Anthony Kramers; John C. Slater (1924). “The Quantum Theory of Radiation”. Philosophical Magazine 47: 785-802. Also Zeitschrift fur Physik, 24, 69 (1924).
- ^ Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 0-19-853907-X
- ^ Heisenberg, W. (1933年). “Heisenberg Nobel lecture”. 2012年12月8日閲覧。
- ^ Mandel, L. (1976). E. Wolf. ed. “The case for and against semiclassical radiation theory”. Progress in Optics. Progress in Optics (North-Holland) 13: 27-69. doi:10.1016/S0079-6638(08)70018-0. ISBN 978-0-444-10806-7.
参考文献[編集]
- Patrick Coffey (2008). Cathedrals of Science. Oxford University Press. ASIN B01FKWEK8U
- 広重 徹『物理学史II』培風館〈新物理学シリーズ〉、1968年。
- 物理学史研究刊行会 編『光量子論』 2巻〈物理学古典論文叢書〉、1969年。
- 物理学史研究刊行会 編『相対論』 4巻〈物理学古典論文叢書〉、1969年。
- 有馬 朗人『量子力学』 4巻、朝倉書店〈朝倉現代物理学講座〉、1994年。
- 水島 宣彦『フォトンの謎 ー光科学の最前線ー』裳華房〈ポピュラーサイエンス〉、1994年。ISBN 4785386053。





