固有振動(こゆうしんどう、英語: characteristic vibration, normal mode)とは対象とする振動系が自由振動を行う際、その振動系に働く特有の振動のことである。このときの振動数を固有振動数という。
振動数[編集]
振動の速さは単位時間に起こる往復運動の回数で表され、この回数を振動数または周波数という。単位はHz(ヘルツ)である。
角振動数[編集]
振動の1回の往復運動は円運動1周に対応していて、振動の速さは単位時間におこなわれる円運動の回転角で表される。これを角振動数という。角振動数は振動数に1周の角度2π(rad)をかけて定義される。単位はrad/sである。
代表的な振動系の固有振動[編集]
ばね‐質量系の固有振動[編集]
 ばね‐質量系の振動
ばね‐質量系の振動
質量mの物体を一端を固定したばね定数kのばねの他端に取り付けて、摩擦の無い水平面上に置く。
右向きを正にx軸をとり、ばねが自然長の時の物体の位置を0とする。
物体を正の向きに移動させるとばねが伸び、負の向きに移動させるとばねは縮む。
いずれもばねはフックの法則に従うため、物体の変位をx、物体がばねから受ける力をFとすると
 … (1-1)
… (1-1)
が成り立つ。また物体の加速度をxの時間tによる2階微分で表すと、
ニュートンの運動方程式は
 … (1-2)
… (1-2)
である。
(1-1)と(1-2)から
 … (1-3)
… (1-3)
を得る。この2階微分方程式を解くと一般解は
 … (1-4)
… (1-4)
となる。ただし は定数で
は定数で である。
このときのωがばね-質量系の固有角振動数である。
である。
このときのωがばね-質量系の固有角振動数である。
単振り子の固有振動[編集]
 単振り子の様子
単振り子の様子
単振り子は微小振動をしているとき水平面内で単振動をしているとみなすことができる。おもり(質点とみなす)の質量をm、糸の長さをℓとする。糸が鉛直線となす角度θが十分小さいとき、水平方向にx軸をとると変位は
 … (2-1)
… (2-1)
水平方向の力は
 … (2-2)
… (2-2)
物体の加速度をxの時間tによる2階微分で表すと、ニュートンの運動方程式は
 … (2-3)
… (2-3)
である。(2-1)、(2-2)、(2-3)から

 … (2-4)
… (2-4)
を得る。この2階微分方程式を解くと一般解は
 … (2-5)
… (2-5)
となる。ただし は定数で
は定数で である。このときのωが単振り子の固有角振動数である。
である。このときのωが単振り子の固有角振動数である。
弦の固有振動[編集]
線密度ρ(kg/m)で張力T(N)で引っ張られている弦に関して、 とおくと
とおくと

の波動方程式を得る。この波動方程式を解くと、
 … (3-1)
… (3-1)
このような各 を基準モードという。また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は
を基準モードという。また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は
 … (3-2)
… (3-2)
(3-1)においてn=1,2,3の基準モードは右図のような振動を示す。
 n=1のとき第1調和振動
n=1のとき第1調和振動
 n=2のとき第2調和振動
n=2のとき第2調和振動
 n=3のとき第3調和振動
n=3のとき第3調和振動
またこの系における固有角振動数は

である。
気柱の固有振動[編集]
空気の密度をρ(g/㎥)、体積弾性率をK(N/㎡)、 とする。ここでは開口で実際に生じる開口端補正を無視して考える。
とする。ここでは開口で実際に生じる開口端補正を無視して考える。
一端が閉口で他端が開口の管[編集]

の波動方程式を得る。この波動方程式を解くと、

また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は

この系における固有角振動数は

である。
両端が開口の管[編集]

の波動方程式を得る。この波動方程式を解くと、

また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は

この系における固有角振動数は

である。
(1-4)式が(1-3)式の解であることの証明[編集]

 … (1-5)
… (1-5)
(1-2)と(1-5)から
 … (1-6)
… (1-6)
(1-6)式で を満足していれば解であることがいえる。
を満足していれば解であることがいえる。
(2-5)式が(2-4)式の解であることの証明[編集]

 … (2-6)
… (2-6)
(2-4)と(2-6)から
 … (2-7)
… (2-7)
(2-7)式で を満足していれば解であることがいえる。
を満足していれば解であることがいえる。
弦に関する波動方程式[編集]
 振動する弦の微小部分
振動する弦の微小部分
波動方程式の導出[編集]
線密度ρ(kg/m)で張力T(N)で引っ張られている弦がXY平面上にあるとする。その弦のxとx+δxの微小部分について考える。位置xにおける弦の接線とx軸のなす角を 、位置x+δxにおける弦の接線とx軸のなす角を
、位置x+δxにおける弦の接線とx軸のなす角を とすると張力
とすると張力 と
と のx方向成分、y方向成分は次のように表すことができる。
のx方向成分、y方向成分は次のように表すことができる。




したがってy方向の力 は
は
 … (3-1)
… (3-1)
ここで にテイラー級数展開を適用すると
にテイラー級数展開を適用すると

δxは微小であるため2次以上の項を無視できる。よって
 … (3-2)
… (3-2)
(3-2)を(3-1)に代入すると、

θ十分に小さいとき と近似できる。また
と近似できる。また と置き換えられるから
と置き換えられるから
 … (3-3)
… (3-3)
線分 の質量は
の質量は であるから[ニュートンの運動方程式は
であるから[ニュートンの運動方程式は

δyが小さいから ,さらに
,さらに =
= とおくと
とおくと
 … (3-4)
… (3-4)
の波動方程式を得る。
波動方程式の解法[編集]
波動方程式を解くために、変数分離法を用いる。
関数y(x,t)がxの関数X(x)とtの関数T(t)の積の形で表されると仮定して
 … (3-5)
… (3-5)
とおく。(3-5)を(3-4)に代入して整理し、両辺をX(x)T(t)でわると
 … (3-6)
… (3-6)
このとき左辺はxのみの関数、右辺はtのみの関数であり、xとtは独立変数である。両辺が等しいということは両辺の値が定数であるということになる。この定数をKとおくと(3-6)から
 … (3-7)
… (3-7)
 … (3-8)
… (3-8)
と書きかえられる。
- xについての方程式
 … (3-7)を解く。
… (3-7)を解く。
ⅰ)K=0のとき

となる。この微分方程式の一般解は である。
である。
ⅱ)K>0のとき
実数の定数k用いて とすると
とすると
 … (3-9)
… (3-9)
と表される。ここで とおくと、
とおくと、 なので(3-9)は
なので(3-9)は と書きかえられる。X(x)は任意の関数であるから
と書きかえられる。X(x)は任意の関数であるから を考える。つまり
を考える。つまり である。したがって解は
である。したがって解は と
と であり、またその線形結合の
であり、またその線形結合の も解である。
も解である。 から
から
 は定数)
は定数)
ⅲ)K<0のとき
実数の定数k用いて とすると
とすると
 … (3-10)
… (3-10)
と表される。ここで とおくと、
とおくと、 なので(3-10)は
なので(3-10)は と書きかえられる。X(x)は任意の関数であるから
と書きかえられる。X(x)は任意の関数であるから を考える。つまり
を考える。つまり である。したがって解は
である。したがって解は と
と であり、またその線形結合の
であり、またその線形結合の も解である。
も解である。 から
から
 は定数)
は定数)
オイラーの公式を適用すると

( はそれぞれ定数)
はそれぞれ定数)
ⅰ)~ⅲ)から
- K=0のとき…
 … (3-11)
… (3-11)
- K>0のとき…
 … (3-12)
… (3-12)
- K<0のとき…
 … (3-13)
… (3-13)
両端固定の長さ の弦について考えると、両端固定による条件は
の弦について考えると、両端固定による条件は
 and
and  … (3-14)
… (3-14)
(3-11)に条件(3-14)を与えると

(3-12)に条件(3-14)を与えると

(3-13)に条件(3-14)を与えると
 or
or 
 は弦が振動していない様子を表すので、振動する弦の解は
は弦が振動していない様子を表すので、振動する弦の解は
 … (3-15)
… (3-15)
である。
- tについての方程式
 … (3-8)を解く。xについての微分方程式を解いたとき、導いた解はK<0のときであった。よってここでもK<0のときのみを考える。実数の定数kを用いて
… (3-8)を解く。xについての微分方程式を解いたとき、導いた解はK<0のときであった。よってここでもK<0のときのみを考える。実数の定数kを用いて とすると(3-8)は
とすると(3-8)は
 … (3-16)
… (3-16)
と表される。この2階微分方程式を解くと一般解は
 … (3-17)
… (3-17)
となる。ただし、 ,
, ,
, は定数で、
は定数で、 である。
である。
(3-15)、(3-17)から
 … (3-18)
… (3-18)
また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は
 … (3-19)
… (3-19)
気柱に関する波動方程式[編集]
波動方程式の導出[編集]
断面積Sの円筒の中の空気の振動を考える。空気の密度をρ[g/㎥]、空気のx軸方向の変位をy(x,t)とする。大気圧を とすると、位置xにおける圧力は
とすると、位置xにおける圧力は と表される。
と表される。
 気柱の変位
気柱の変位
この円筒の中のxとx+δxの微小部分について考える。空気が振動していないとき微小部分の体積はV=Sδxである。空気が振動したときの体積の変化は
 … (4-1)
… (4-1)
と表される。空気の体積と圧力の間には
 … (4-2)
… (4-2)
の関係が成り立つ。ここでKは体積弾性率である。(4-1)を(4-2)に代入すると

δx→0で
 … (4-3)
… (4-3)
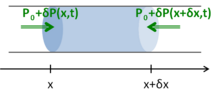 気柱にはたらく圧力
気柱にはたらく圧力
空気の断面にはそれぞれ圧力がはたらいている。xにおける断面にはたらく力は

x+δxにおける断面にはたらく力は

したがって微小部分にはたらく力は
 … (4-4)
… (4-4)
また微小部分の質量は であり、ニュートンの運動方程式を整理すると
であり、ニュートンの運動方程式を整理すると

x→0で
 … (4-5)
… (4-5)
(4-3),(4-5)より

 =
= とおくと
とおくと
 … (4-6)
… (4-6)
の波動方程式を得る。
波動方程式の解法[編集]
「弦に関する波動方程式の解法」と同様にして変数分離法で波動方程式を解いていくと、xについての方程式は次の解を得る。
- K=0のとき…
 … (4-7)
… (4-7)
- K>0のとき…
 … (4-8)
… (4-8)
- K<0のとき…
 … (4-9)
… (4-9)
一端が閉口で他端が開口の管の場合[編集]
ここでは開口で実際に生じる開口端補正を無視して解きすすめる。左端が閉口で右端が開口な長さ の管について考えると、左端が閉口による条件は
の管について考えると、左端が閉口による条件は 、右端が開口による条件は
、右端が開口による条件は つまり
つまり 。したがって管の満たすべき条件は
。したがって管の満たすべき条件は
 and
and  … (4-10)
… (4-10)
である。(4-7)に条件(4-10)を与えると

(4-8)に条件(4-10)を与えると

(4-9)に条件(4-10)を与えると
 or
or 
 は気柱が振動していない様子を表すので、振動する気柱の解は
は気柱が振動していない様子を表すので、振動する気柱の解は
 … (4-11)
… (4-11)
である。また、「弦に関する波動方程式の解法」と同様にしてtについての方程式を解くと、
 … (4-12)
… (4-12)
となる。ただし、 ,
, ,
, は定数で、
は定数で、 である。したがって
である。したがって
 … (4-13)
… (4-13)
また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は
 … (4-14)
… (4-14)
両端が開口の管の場合[編集]
ここでは開口で実際に生じる開口端補正を無視して解きすすめる。両端が開口で長さ の管について考えると、両端開口による条件は
の管について考えると、両端開口による条件は
 and
and  … (4-15)
… (4-15)
である。(4-7)に条件(4-15)を与えると

(4-8)に条件(4-15)を与えると

(4-9)に条件(4-15)を与えると
 or
or 
 は気柱が振動していない様子を表すので、振動する気柱の解は
は気柱が振動していない様子を表すので、振動する気柱の解は
 … (4-16)
… (4-16)
である。また、「弦に関する波動方程式の解法」と同様にしてtについての方程式を解くと、
 … (4-17)
… (4-17)
となる。ただし、 ,
, ,
, は定数で、
は定数で、 である。したがって
である。したがって
 … (4-18)
… (4-18)
また各y(x,t)は線形微分方程式の解であるから、それらの和もまた解である。したがって一般解は
 … (4-19)
… (4-19)
参考文献[編集]
| 出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。記事の信頼性向上にご協力をお願いいたします。(2023年3月) |
関連項目[編集]







































































































































