音程
音程(おんてい、英語: Interval〈インターバル〉)とは、二つの音の高さの隔たりのことである。この記事では伝統的な西洋音楽において一般的な、半音を最小単位として構成される音程について記述する。
順次的に鳴る音に対する音程を旋律的音程と呼び、同時に鳴る音に対する音程のことを和声的音程と呼ぶ[1]。
音程の名称[編集]
音程の名称は、基本的には五線譜上での隔たりで「◯度」という名称が決まる。1オクターヴ以下の音程を単音程と呼び、それ以上離れているときを複音程という。
度数[編集]

2つの音が譜面上の同一の高さの位置にあるとき、「0度」ではなく「1度」である。つまり、2つの幹音(譜面上でシャープやフラットがつかない音)が譜面上n個離れているとき、その2つの音はn+1度の関係にある。
例えば右の図の2つの音は1オクターヴであるが、譜面上7つ(線3つと線の間4つ)離れており、音程は7+1で「8度」となる。
単音程の名称[編集]
度数に「短」「長」「完全」「増」「減」といった接頭辞をつけて音程を表す。
「短」「長」といった接頭辞をつけるのは下記の理由による。

右の図のように、幹音上の2度の音のペアは7組あるが、ミ〜ファとシ〜ドは半音で、それ以外のペアは2半音=全音離れている。前者を短2度、後者を長2度と呼ぶ[2]。
同様に、幹音上の3度ではミ〜ファとシ〜ドという半音区間を含むレ〜ファ、ミ〜ソ、ラ〜ドは3半音と狭く、半音区間を含まないド〜ミ、ファ〜ラ、ソ〜シは4半音と広いため、前者を短3度、後者を長3度と呼ぶ。

6度、7度も同様の理由から、幹音上には半音異なった大小2種類の音程があるので、狭い方に「短」・広い方に「長」という接頭辞をつける。
4度と5度[編集]
4度と5度も幹音上には2種類の音程があるが、完全協和音程を含むため、「完全」・「増」・「減」の接頭辞を用いる。
- 4度の場合、ド〜ファ、レ〜ソなど、半音区間を含み完全協和音程の5半音の方を「完全4度」、半音区間を含まないファ〜シの6半音の方を「増4度」と呼ぶ[2]。
- 5度の場合、半音区間を2回含み6半音のシ〜ファを「減5度」、それ以外の半音区間を1回だけ含むド〜ソなど完全協和音程の7半音の方を「完全5度」と呼ぶ[2]。
1度と8度[編集]
1度と8度の場合は、幹音上に完全協和音程の一種類(1度なら0半音、8度なら12半音)しかないので、1度のペア(=同一の音)を「完全1度」、8度離れたペアの事を「完全8度」という[2]。1度は「同度」、「ユニゾン」とも呼ぶ。
増4度と減5度[編集]
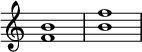
前述のように「増4度」と「減5度」はいずれも12平均律では6半音で同じ音程だが、譜面上は異なる。例えば右図の2組の音のペアはいずれも6半音差だが、譜面上は左は4度なので「増4度」、右は5度なので「減5度」と呼ぶ。三全音(トライトーン)とも呼ぶ。
「増」「減」「重増」「重減」[編集]
- 長または完全より半音広い音程に増(ぞう)、2半音広い音程に重増(じゅうぞう)という接頭辞を付けて呼ぶ(例:増7度、重増7度、増5度、重増5度)。
- 短または完全より半音狭い音程に減(げん)、2半音狭い音程に重減(じゅうげん)という接頭辞を付けて呼ぶ。
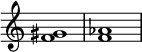
これらの名称は例えばシャープやフラットなどの変化記号がついたときに用いる。
例えば右図で「増2度」と「短3度」はいずれも12平均律では3半音で同一の音程であるが、譜面上は左は「2度」は右は「3度」なので、左を「増2度」と右を「短3度」と呼ぶ。
| 0半音 | 1半音 | 2半音 | 3半音 | 4半音 | 5半音 | 6半音 | 7半音 | 8半音 | 9半音 | 10半音 | 11半音 | 12半音 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 完全1度 | 短2度 | 長2度 | 短3度 | 長3度 | 完全4度 | 減5度 増4度 |
完全5度 | 短6度 | 長6度 | 短7度 | 長7度 | 完全8度 |
複音程[編集]
2つの音の高さが13半音以上、すなわち1オクターヴより大きく離れている場合を複音程と呼び、「3オクターヴと完全4度」のようにオクターヴ数と単音程の組み合わせにより複音程を表す。
ただし、「9度のような若干の複音程は和声の特徴的な要素なので、大きいほうの数でよばれるのが普通である」[引用 1]ので、例えば「1オクターブと短3度」の事を「短10度」と呼ぶ。
協和音程と周波数比[編集]
2つの音の周波数の比率が簡単な整数比で表せない場合、その2つの音を同時に鳴らすとうなりが発生してしまう。このため西洋音楽の和音では同時に鳴らす音の周波数比が単純であればあるほど、より「協和」した音程として重視してきた[注 2]。
このため整数比の簡単さ(=「協和」)の度合いにより、音程を以下のように分類する[2]:
| 音程 | 周波数比 | ||
|---|---|---|---|
| 協和音程 | 完全協和音程 | 完全1度 | 1:1 |
| 完全8度 | 1:2 | ||
| 完全5度 | 2:3 | ||
| 完全4度 | 3:4 | ||
| 不完全協和音程 | 長3度 | 4:5 | |
| 短3度 | 5:6 | ||
| 長6度 | 3:5 | ||
| 短6度 | 5:8 | ||
| 不協和音程 | それ以外 | - | |
完全1度・完全8度を特に絶対協和音程という。
転回音程[編集]
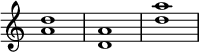
2つの音のペアのうち高い方の音を1オクターブ下げる事を転回(てんかい)という。たとえば「C」と「E」のペアがあるとき、高い方の音であるEを「1オクターブ低いE」と(元のオクターブと同じ)「C」のペアが元のペアの転回になる。音程を転回することで、その結果生じる音程を転回音程(てんかいおんてい)という[2]。
なお、2つの音の両方を1オクターブずらしても音程は変わらないので、高い方の音を1オクターブ下げるかわりに低い方の音を1オクターブ上げても転回になる[注 4]。
2つの音のペアがn半音離れているとき、転回したペアは12-n半音離れている事になるので、以下のようになる。
| 元の音階 | 転回音階 |
|---|---|
| 完全1度 | 完全8度 |
| 短2度 | 長7度 |
| 長2度 | 短7度 |
| 短3度 | 長6度 |
| 長3度 | 短6度 |
| 完全4度 | 完全5度 |
なお、転回音階の転回音階は元に戻る。上述の対応からわかるように、転回音程の名称を以下のようにして求める事ができる:
- 元の音程がm度であれば、転回音程は9-m度である。
- 長←→短、増←→減、重増←→重減という入れ替えを行う。
- 元の音程が「完全」であれば転回音程も「完全」にする。
なお、転回はペアの一方の1つの音を1オクターブの上げ下げする行為であり、1オクターブ上げるのは周波数を2倍する行為なので、周波数比がa:bである音のペアを転回すると周波数比がb:2aになる。
全音階的音程と半音階的音程[編集]
音程には、全音階の中に現れる音程とそうでない音程があり、前者を全音階的音程、後者を半音階的音程と呼ぶことがある。すべての完全音程、長音程、短音程と、増4度、減5度が全音階的音程で、それ以外が半音階的音程である。 下に、長音階に現れる各音程の一覧を示した。
| 下の音\上の音 | C | D | E | F | F | A | B |
|---|---|---|---|---|---|---|---|
| C | 完全8度 | 長2度 | 長3度 | 完全4度 | 完全5度 | 長6度 | 長7度 |
| D | 短7度 | 完全8度 | 長2度 | 短3度 | 完全4度 | 完全5度 | 長6度 |
| E | 短6度 | 短7度 | 完全8度 | 短2度 | 短3度 | 完全4度 | 完全5度 |
| F | 完全5度 | 長6度 | 長7度 | 完全8度 | 長2度 | 長3度 | 増4度 |
| G | 完全4度 | 完全5度 | 長6度 | 短7度 | 完全8度 | 長2度 | 長3度 |
| A | 短3度 | 完全4度 | 完全5度 | 短6度 | 短7度 | 完全8度 | 長2度 |
| B | 短2度 | 短3度 | 完全4度 | 減5度 | 短6度 | 短7度 | 完全8度 |
音程の単位[編集]
上では伝統的な音程の名称を説明したが、より定量的な方法で音程を定義する単位としてセントがある。セントは、1オクターブが1200セントになるように定義される。平均率の半音はその1/12なので、100セントとなる。
セントは厳密には周波数の対数により定義される。2つの音の周波数比がRであるとき、その2つの音の音程のセントは:
により定義される[5]。
日本語とヨーロッパ主要言語における表現[編集]
| 日本語 | Latina (ラテン語) | Italiano (イタリア語) | Français (フランス語) | Deutsch (ドイツ語) | English (英語) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 音程 | Intervallum | Intervallo | Intervalle | Intervall | Interval | ||||||
| 重増 - | (重増) | - più che aumentato/a (più che eccedente) | - sur-augmenté | doppelt übermäßige - | doubly augmented - | ||||||
| 増 - | - augmentur | - aumentato/a (eccedente) | - augmentée | übermäßige - | augmented - | ||||||
| 長 - | 完全 - | - maior | - iustus | - maggiore | - giusto/a | - majeure | - juste | große - | rein - | major - | perfect - |
| 短 - | - minor | - minore | - mineure | kleine - | minor - | ||||||
| 減 - | - deminutur | - diminuito/a | - diminuée | verminderte - | diminished - | ||||||
| 重減 - | (重減) | - più che diminuito/a | - sous-diminué | doppelt verminderte - | doubly diminished - | ||||||
| 15度 | quintusdecimus | quindicesima | quinzième | quindezime | fifteenth | ||||||
| 14度 | quartusdecimus | quattordicesima | quatorzième | quardezime | fourteenth | ||||||
| 13度 | tertiusdecimus | tredicesima | treizième | tredezime | thirteenth | ||||||
| 12度 | duodecimus | dodicesima | douzième | duodezime | twelfth | ||||||
| 11度 | undecimus | undicesima | onzième | undezime | eleventh | ||||||
| 10度 | decimus | decima | dixième | dezime | tenth | ||||||
| 9度 | nonus | nona | neuvième | none | ninth | ||||||
| 8度 | octavus | ottava | octave | oktave | octave | ||||||
| 7度 | septimus | settima | septième | septime | seventh | ||||||
| 6度 | sextus | sesta | sixte | sexte | sixth | ||||||
| 5度 | quintus | quinta | quinte | quinte | fifth | ||||||
| 4度 | quartus | quarta | quarte | quarte | fourth | ||||||
| 3度 | tertius | terza | tierce | terz | third | ||||||
| 2度 | secundus | seconda | seconde | sekunde | second | ||||||
| 同度 | unisonus | unisono | unisson | unisono | unison | ||||||
脚注[編集]
引用[編集]
- ^ ピストン、デヴォート『和声法 分析と実習』音楽之友社、2006年6月。ISBN 9784276103214。
出典[編集]
注釈[編集]
- ^ 同じ音のときに「0半音」としている
- ^ 具体的には2つの音の周波数がそれぞれnA、mAであるとき、nとmの最小公倍数をとすると、2つの音を同時に鳴らしたときの周波数はである。
- ^ 音律が純正律であれば、2つの幹音の周波数比は常に整数になるが、平均律であれば、n半音差のある2つの音の周波数比はであるので、nが12の倍数でない限り(i.e.度数が7度の倍数+1でない限り)完全な整数比になる事はありえない。ただし純正律と平均律はほぼ等しいので、平均律の場合も周波数比はほぼ整数になる。
- ^ 例えば「C」「E」というペアの転回は「1オクターブ低いE」と「元のオクターブのC」のペアだが、このペアの両方の音を1オクターブ上げても音程は変わらないので、両方1オクターブ上げると「元のオクターブE」と「1オクターブ高いC」のペアになる。 よって結局転回は「低い方の音(この場合C)を1オクターブ上げる」という事と同じになる。
参考文献[編集]
- 小方厚『音律と音階の科学 新装版 ドレミ…はどのように生まれたか』講談社〈ブルーバックス〉、2018年5月16日。ISBN 978-4065116647。
- “楽譜について学ぶ 第3日 音程”. MUSIC PAL - 学校音楽教育支援サイト. ヤマハ. 2023年9月25日閲覧。
- ピストン、デヴォート『和声法 分析と実習』音楽之友社、2006年6月。ISBN 9784276103214。
- 石桁真礼生、末吉保雄『楽典 理論と実習』音楽之友社、2016年。ISBN 4-276-10000-3。




