円に内接する四角形

円に内接する四角形(えんにないせつするしかっけい、英: cyclic quadrilateral)または単に内接四角形(ないせつしかっけい、英: inscribed quadrilateral)とは、4頂点が1つの円周上にある四角形のことである[1]。この円のことを外接円といい、その上にある4頂点は共円であるという。一般的に、内接四角形は凸であると仮定されるが、四角形が自己交差することを許せば凸でない内接四角形も存在する。以下では凸四角形に限って述べることとする。
すべての三角形が外接円を持つのに対して、すべての四角形が外接円を持つとは限らない。たとえば、正方形でない菱形は内接四角形ではないが、正方形・長方形・等脚台形・反平行四辺形はすべて内接四角形である。凧形が内接四角形となるための必要十分条件は、それが二つの直角を持つことである(直角凧形)。双心四角形は内接四角形であり、かつ外接四角形でもある。傍双心四角形は内接四角形であり、かつ傍接四角形でもある。調和四角形は内接四角形であって対辺の長さの積が等しいものである。
特徴付け[編集]

- 凸四角形が内接四角形であるための必要十分条件は四つある辺の垂直二等分線が共点となる(つまり一点で交わる)ことである。このとき共有される点は外心と呼ばれる[2]。
- 凸四角形 □ABCD が内接四角形となるための必要十分条件は、その向かい合う角が互いに補角となることである。式で書けば、四つの角が隣り合う順に α, β, γ, δ の角度を持つとすれば と書ける[2]。直接の定理はエウクレイデスの『原論』第3巻の命題22[3]であるが、同値な言い換えとして、凸四角形が内接四角形となるための必要十分条件は、その各外角が内対角に等しいことである。
- 凸四角形 □ABCD が内接四角形となる別の必要十分条件は、ひとつの辺と一方の対角線との間の角が対辺と他方の対角線との間の角に等しいことである[4]。つまり例えば のときはそうである。
- トレミーの定理の述べるところは、内接四角形のふたつの対角線の長さ e, f の積は、二組ある対辺の長さの積の和に等しいことである。式では と書ける[5]:25。逆もまた成り立ち、この式を満たす凸四角形は内接四角形となる。
- 二つの直線があり、一方が線分 AC を他方が線分 BD を含み、点 P で交わるとする。このとき四点 A, B, C, D が共円となるための必要十分条件は、線分の長さについて が成り立つことである[6]:179。このとき、交点 P は四点が存在する円の内部にも外部にも位置しうる。前者の場合では □ABCD が内接四角形となり、後者の場合では □ABDC が内接四角形を成す。また前者の場合において上記の等式は、一方の対角線を P で分割して得られる線分の長さの積が他方のそれと等しいことを述べるものとなる。このことは、この内接四角形の対角線が外接円の弦であることから交弦定理と呼ばれる。
- もっとほかの特徴づけとして、凸四角形 □ABCD が内接四角形となるための必要十分条件は が成り立つことである[7]。
面積公式[編集]
内接四角形の面積 K は、その四辺の長さを a, b, c, d とすれば、ブラーマグプタの公式により
内接四角形は、各辺がそれぞれ決まった長さの並びであるようなすべての四角形の中で最大の面積を持つ(これもまたブレートシュナイダーの公式の系であるし、微分積分学を用いても証明できる)[8]。
ブラーマグプタの公式を見れば、各辺の長さがどの二つも異なり他の三つの辺の長さの和よりも小さいという条件のもとで、そのような長さの辺を持つ内接四角形は面積が決まれば合同の違いを除いて三種類しかないことが分かる[9]。具体的に言えば、各辺の長さが隣り合う順に a, b, c, d であったときに、長さ a の辺と残りの長さ b, c, d の辺のどれとでもよいから入れ替えるならば、面積は同じで、しかも合同にはならない。
内接四角形の面積は、辺の長さが隣り合う順に a, b, c, d で長さ a および b の辺の成す角度が B であるとき
もっと別の形では、外半径を R として、
対角線公式[編集]
内接四角形の頂点が隣り合う順に A, B, C, D であり、各辺の長さを a ≔ AB, b ≔ BC, c ≔ CD, d ≔ DA とするとき、対角線の長さ p ≔ AC, q ≔ BD は辺の長さを用いて
対角線の長さの和に関して不等式
任意の凸四角形が二つの対角線によって四つの三角形に分割されるが、内接四角形においてそれら四つの三角形の向かい合う対は互いに相似になる。
二つの対角線 AC, BD の中点をそれぞれ M, N とすれば
内接四角形を成す辺の集合が一つ与えられれば、それらの並びだけを替えて、外接円と面積を変えることなく、三つの相異なる内接四角形を作ることができる(面積が変わらないことはブラーマグプタの公式からわかる)。そのような内接四角形のどの二つも、ひとつの対角線の長さは共通である[13]:p84。
角公式[編集]
内接四角形の辺の長さが隣り合う順に a, b, c, d で与えられているものとし、半周長を s と書く。
- a, d の二辺の間の角 ∠A における各三角比の値は で与えられる[17]:202。
- 二つの対角線の成す角度を θ とすれば が成り立つ[5]:26。
- 向かい合う二辺 a, c を延長した直線が角度 φ で交わるならば が成り立つ[5]:31。
パラメシュヴァーラの外半径公式[編集]
内接四角形の辺を隣り合う順に a, b, c, d とし、その半周長を s ≔ (a + b + c + d)/2 と書けば、その四角形の外半径(外接円の半径)R は
ブラーマグプタの公式を用いれば、上記の公式は
反中心・共線性[編集]
四角形において、一辺に垂直で対辺の中点を通る線分は(「中点からの垂線」の短縮形として)中垂線 (maltitude) と呼ばれる[19]。内接四角形の各辺に引いた四つの中垂線は一点で交わる[20]:p.131[21]。このときの共通交点は反中心 (anticenter) と呼ばれる。反中心は、「頂点重心」の外心に関する鏡像になっているという特徴を持つ点である。したがって、内接四角形では外心、「頂点重心」、反中心は同一直線上にある[21]。
内接四角形のふたつの対角線の交点を P とし、対角線の中点をそれぞれ M, N とするならば、その内接四角形の反中心は三角形 △MNP の垂心に一致する。
その他の性質[編集]
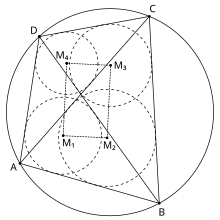
- 内接四角形 □ABCD において、四つの三角形 △DAB, △ABC, △BCD, △CDA の内心をそれぞれ M1, M2, M3, M4 とすれば、この四点を頂点とする四角形は長方形になる。これは日本人の定理と呼ばれる定理のひとつで、丸山良寛の定理と呼ばれる。同じ四つの三角形の、こんどは垂心を考えればそれらを頂点とする四角形は □ABCD に合同であり、また重心で同様に考えれば別の内接四角形となる[4]。
- 内接四角形 □ABCD の外心を O とし、二つの対角線 AC と BD の交点を P とするとき、∠APB の角度は ∠AOB と ∠COD の算術平均である。これは円周角の定理と外角定理からの直接の帰結である。
- 面積が有理数で、どの二つも相異なる有理数の長さの辺となるような四角形で、その辺の長さが算術数列または幾何数列を成すとき、そのような四角形は共円でない[22]。
- 内接四角形の辺の長さが算術数列を成すならば、その四角形は傍接四角形(したがって、傍双心四角形)である。
- 内接四角形の二組の向かい合う辺を延長して、それらがそれぞれ点 E, F で交わるならば、E および F のそれぞれにおいてなす角の二等分線は直交する[9]。
ブラーマグプタの四角形[編集]
ブラーマグプタ (Brahmagupta) の四角形とは、辺の長さおよび対角線の長さが全て整数で面積も整数となる内接四角形をいう[23]。すべてのブラーマグプタの四角形は、その辺の長さを a, b, c, d, 対角線の長さを e,f とし、面積を K, 外半径を R と書けば、有理数の範囲を動くパラメータ t, u, v を用いて書ける以下の公式
対角線が直交する場合[編集]
外半径と面積[編集]
内接四角形でなおかつ直交対角線である(つまり二つの対角線が互いに垂直である)ようなものに対し、二つの対角線の交点が一方の対角線を長さ p1 および p2 の線分に分け、他方の対角線を長さ q1 および q2 の線分に分けるものとすると
円に内接する直交対角線四角形の面積 K を四辺の長さで表す公式は、トレミーの定理と直交対角線四角形の面積公式を組合わせることで直接的に得られる。それは
その他の性質[編集]
- 円に内接する直交対角線四角形において、反中心は対角線の交点となる点に一致する[20]。
- ブラーマグプタの定理の述べるところによれば、内接四角形がさらに対角線直交であるならば、対角線の交点から任意の辺に下ろした垂線は対辺を二等分する[20]。
- 内接四角形が直交対角線でもあるならば、外心から任意の辺へ測った距離は対辺の長さの半分に等しい[20]。
- 円に内接する直交対角線四角形において、二つの対角線それぞれの中点同士の距離は、外心と対角線の交点との距離に等しい[20]。
球面内接四角形[編集]
球面幾何学において、交わる四つの大円から形作られる球面四角形が内接四角形となるための必要十分条件は、二組の向かい合う角の和が等しい(つまり、隣り合う順に四つの角度が α, β, γ, δ であるとき、α + γ = β + δ となる)ことである[26]。この定理の一つの方向は1786年に I. A. Lexell が示した[27]。(Lexell 1786) では、球の小円に内接する球面四角形において向かい合う角の和が等しいことおよび外接する球面四角形において向かい合う辺の和が等しいことが示されている。この二つの定理について、前者は平面幾何における同様の定理の球面幾何版であり、後者は前者の双対(つまり大円と極点との役割をいれかえたもの)になっている[28]。Kiper らはこの定理の逆「球面四角形において向かい合う辺の長さの和が等しいならば、この球面四角形に内接する円が存在する」を示した[29]。
関連項目[編集]
- 胡蝶定理
- 内接多角形
- 方冪の定理
- プトレマイオスの弦の数表
- ロビンスの五角形: 辺および面積が有理数の共円五角形
注[編集]
注釈[編集]
出典[編集]
- ^ 安藤, 哲哉『三角形と円の幾何学: 数学オリンピック幾何問題完全攻略』海鳴社、東京、2006年、123頁。ISBN 4-87525-234-X。OCLC 676371564。
- ^ a b Usiskin et al. 2008.
- ^ Joyce, D. E. (June 1997), “Book 3, Proposition 22”, Euclid's Elements, Clark University
- ^ a b Andreescu & Enescu 2004.
- ^ a b c d e f g h i Durell & Robson 2003.
- ^ Bradley 2007.
- ^ Hajja, Mowaffaq (2008), “A condition for a circumscriptible quadrilateral to be cyclic”, Forum Geometricorum 8: 103–106
- ^ Peter, Thomas (September 2003), “Maximizing the area of a quadrilateral”, The College Mathematics Journal 34 (4): 315–6, doi:10.2307/3595770, JSTOR 3595770
- ^ a b Coxeter & Greitzer 1967.
- ^ Prasolov, Viktor, Problems in plane and solid geometry: v.1 Plane Geometry
- ^ Alsina & Nelsen 2009.
- ^ a b c Alsina & Nelsen 2007.
- ^ a b Johnson 2007.
- ^ a b Inequalities proposed in "Crux Mathematicorum", 2007, [1].
- ^ “ABCD is a cyclic quadrilateral. Let M, N be midpoints of diagonals AC, BD respectively...”, Art of Problem Solving, (2010)
- ^ A. Bogomolny, An Identity in (Cyclic) Quadrilaterals, Interactive Mathematics Miscellany and Puzzles, [2], Accessed 18 March 2014.
- ^ Siddons & Hughes1929.
- ^ Hoehn 2000.
- ^ Weisstein, Eric W. "Maltitude". mathworld.wolfram.com (英語).
- ^ a b c d e f g Altshiller-Court 2007.
- ^ a b Honsberger 1995.
- ^ Buchholz & MacDougall 1999.
- ^ Sastry, K.R.S. (2002). “Brahmagupta quadrilaterals”. Forum Geometricorum 2: 167–173.
- ^ Posamentier & Salkind 1970.
- ^ Josefsson, M. (2016), “Properties of Pythagorean quadrilaterals”, The Mathematical Gazette 100 (July): 213–224, doi:10.1017/mag.2016.57
- ^ Wimmer, Lienhard (2011). “Cyclic polygons in non-Euclidean geometry”. Elemente der Mathematik 66 (2): 74–82.
- ^ Lexell, A. J. (1786). “De proprietatibus circulorum in superficie sphaerica descriptorum”. Acta Acad. Sci. Petropol. 6 (1): 58–103.
- ^ Rosenfeld, B. A. (1988). A History of Non-Euclidean Geometry - Springer. Studies in the History of Mathematics and Physical Sciences. 12. doi:10.1007/978-1-4419-8680-1. ISBN 978-1-4612-6449-1
- ^ Kiper, Gökhan; Söylemez, Eres (2012-05-01). “Homothetic Jitterbug-like linkages”. Mechanism and Machine Theory 51: 145–158. doi:10.1016/j.mechmachtheory.2011.11.014.
参考文献[編集]
- Alsina, C.; Nelsen, R. B. (2007), “On the diagonals of a cyclic quadrilateral”, Forum Geometricorum 7: 147–149
- Alsina, Claudi; Nelsen, Roger (2009), “4.3 Cyclic, tangential, and bicentric quadrilaterals”, When Less is More: Visualizing Basic Inequalities, Mathematical Association of America, pp. 64–66, ISBN 978-0-88385-342-9
- Altshiller-Court, N. (2007) [1952], College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), Courier Dover, pp. 131, 137–138, ISBN 978-0-486-45805-2, OCLC 78063045
- Andreescu, T.; Enescu, B. (2004), “2.3 Cyclic quads”, Mathematical Olympiad Treasures, Springer, pp. 44–46, 50, ISBN 978-0-8176-4305-8, MR2025063
- Bradley, C. J. (2007), The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates, Highperception, ISBN 978-1906338008, OCLC 213434422
- Buchholz, R. H.; MacDougall, J. A. (1999), “Heron quadrilaterals with sides in arithmetic or geometric progression”, Bulletin of the Australian Mathematical Society 59 (2): 263–269, doi:10.1017/S0004972700032883, MR1680787
- Coxeter, H. S. M.; Greitzer, S. L. (1967), “3.2 Cyclic Quadrangles; Brahmagupta's formula”, Geometry Revisited, Mathematical Association of America, pp. 57–60, ISBN 978-0-88385-619-2
- Durell, C. V.; Robson, A. (2003) [1930], Advanced Trigonometry, Courier Dover, ISBN 978-0-486-43229-8
- Hoehn, L. (March 2000), “Circumradius of a cyclic quadrilateral”, Mathematical Gazette 84 (499): 69–70, doi:10.2307/3621477, JSTOR 3621477
- Honsberger, Ross (1995), “4.2 Cyclic quadrilaterals”, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, New Mathematical Library, 37, Cambridge University Press, pp. 35–39, ISBN 978-0-88385-639-0
- Johnson, R. A. (2007) [1929], Advanced Euclidean Geometry, Dover Publ.
- Posamentier, A. S.; Salkind, C. T. (1970), “Solutions: 4-23 Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.”, Challenging Problems in Geometry (2nd ed.), Courier Dover, pp. 104–5, ISBN 978-0-486-69154-1
- Siddons, A. W.; Hughes, R. T. (1929), Trigonometry, Cambridge University Press, OCLC 429528983
- Usiskin, Z.; Griffin, J.; Witonsky, D.; Willmore, E. (2008), “10. Cyclic quadrilaterals”, The Classification of Quadrilaterals: A Study of Definition, Research in mathematics education, IAP, pp. 63–65, ISBN 978-1-59311-695-8
外部リンク[編集]
- Derivation of Formula for the Area of Cyclic Quadrilateral
- Incenters in Cyclic Quadrilateral at cut-the-knot
- Four Concurrent Lines in a Cyclic Quadrilateral at cut-the-knot
- Weisstein, Eric W. "Cyclic Quadrilateral". mathworld.wolfram.com (英語).
- cyclic quadrilateral - PlanetMath.(英語)
- Definition:Cyclic quadrilateral at ProofWiki
- Euler centre and maltitudes of cyclic quadrilateral at Dynamic Geometry Sketches, interactive dynamic geometry sketch.
























![{\displaystyle {\begin{aligned}a&=[t(u+v)+(1-uv)][u+v-t(1-uv)]\\b&=(1+u^{2})(v-t)(1+tv)\\c&=t(1+u^{2})(1+v^{2})\\d&=(1+v^{2})(u-t)(1+tu)\\e&=u(1+t^{2})(1+v^{2})\\f&=v(1+t^{2})(1+u^{2})\\K&=uv[2t(1-uv)-(u+v)(1-t^{2})][2(u+v)t+(1-uv)(1-t^{2})]\\4R&=(1+u^{2})(1+v^{2})(1+t^{2})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e69092a26a00ae86a1b49767f2aab465ad93479)





