十二芒星
| Regular dodecagram | |
|---|---|
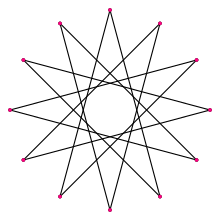 A regular dodecagram | |
| 種類 | 星型正多角形 |
| 辺・頂点 | 12 |
| シュレーフリ記号 | {12/5} t{6/5} |
| コクセター図形 | |
| 対称性群 | 二面体 (D12) |
| 内角 (度) | 30° |
| 双対多角形 | 自己双対 |
| 要素 | 星型、円型、等辺、等角、同辺 |
十二芒星(じゅうにぼうせい、英語:dodecagram ドデカグラム)は、12個の頂点を持つ星型多角形。シュレーフリ記号は{12/5}である。正十二芒星は{12/1}で表される正十二角形と同じ頂点の配置を持つ。
等角の変形[編集]
正十二芒星は、準切頂(quasitruncated)六角形として見なすことができ、t{6/5}={12/5}である。等間隔の頂点を持つ他の等角(頂点推移)の変形例は、2つの辺長で構成することができる。
 t{6} |

|

|
 t{6/5}={12/5} |
組み合わせによる十二芒星[編集]
4つの正十二芒星の星形がある。{12/2}=2{6}, {12/3}=3{4}, {12/4}=4{3}, {12/6}=6{2}。1番目は2つの六角形を組み合わせたもの、2番目は3つの正方形を組み合わせたもの、3番目は4つの三角形を組み合わせたもの、4番目は6つの直線状の二角形を組み合わせたものである。最後から2番目は2つの六芒星、最後は3つの四芒星を組み合わせたものと考えることもできる。
 2{6} |
 3{4} |
 4{3} |
 6{2} |
完全グラフ[編集]
十二角形と十二芒星(6つの二角形(線分)の退化した組み合わせを含む)を全て重ね合わせると完全グラフK12が生成される。

|
黒: 12個の頂点(節点) 赤: {12} 正十二角形 |
多面体の正十二芒星[編集]
十二芒星は、一様多面体に組み込むこともできる。以下は正十二芒星を含む柱状一様多面体である(他に十二芒星を含む一様多面体はない)。
ユークリッド平面のスター・テッセレーションに組み込むこともできる。
象徴としての十二芒星[編集]

十二芒星もしくは12個の点を持つ星は次に示す象徴で使用されている。
- the twelve tribes of Israel, in Judaism
- the twelve disciples, in Christianity
- the twelve olympians, in Hellenic Polytheism
- the twelve signs of the zodiac
- the International Order of Twelve Knights and Daughters of Tabor, an African-American fraternal group
- the fictional secret society Manus Sancti, in the Knights of Manus Sancti series by Bryn Donovan
関連項目[編集]
出典[編集]
- Weisstein, Eric W. "Dodecagram". mathworld.wolfram.com (英語).
- Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)



