出典: フリー百科事典『ウィキペディア(Wikipedia)』
| この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: "ブレートシュナイダーの公式" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2016年5月) |
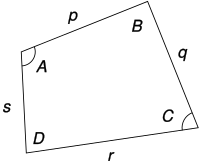 p, q, r, s, A, C の値から四角形の面積が求まる。
p, q, r, s, A, C の値から四角形の面積が求まる。
ブレートシュナイダーの公式(ブレートシュナイダーのこうしき、Bretschneider's formula)は、四角形の面積を与える公式である。四角形ABCD について、p, q, r, s をそれぞれの辺の長さ、T を半周長、A と C を互いに対角とすると、四角形の面積は

に等しい。円に内接する四角形の面積を表したブラーマグプタの公式の一般化であり、任意の四角形について成り立つ。名前の由来はドイツの数学者カール・アントン・ブレートシュナイダー(1808–1878)にちなむ。
四角形の面積を S とすると、
 (±は、凸四角形と凹四角形の場合を省略します)
(±は、凸四角形と凹四角形の場合を省略します)
より

を得る。また、余弦定理より、

であるから

を得る。4S2 についての式と辺々を足し合わせ、加法定理 cos(A + C) = cos A cos C − sin A sin C を用いると、

となる。倍角の公式  を用いて変形すると、
を用いて変形すると、

となる。この式は、半周長

を用いて

となり、ブレートシュナイダーの公式を得る。
関連する公式[編集]
円に内接する四角形については、対角の和の半分が 90°であることから、ブラーマグプタの公式
- S = √(T − p)(T − q)(T − r)(T − s)
が成り立つ。また、円に外接する四角形については、対辺の和が等しく、T = p + r = q + s であることから

が成り立つ。さらに外接円と内接円を持つ四角形、つまり双心四角形については、
- S = √pqrs
となる。また、上記の証明は p = 0 として三角形の面積を考えているとしても通用し、ヘロンの公式
- S = √T(T − q)(T − r)(T − s)
を得る。
参考文献[編集]
関連項目[編集]
外部リンク[編集]













