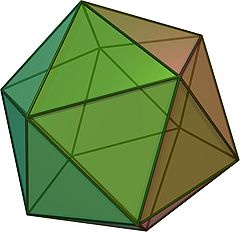
正二十面体

正二十面体
	;
種別	正多面体、デルタ多面体、二十面体
面形状	20枚の正三角形
辺数	30
頂点数	12
頂点形状	35;
シュレーフリ記号	{3, 5}
ワイソフ記号	5 \| 2 3
対称群	Ih
双対多面体	正十二面体
特性	凸集合
	; 展開図
	テンプレートを表示

正二十面体（せいにじゅうめんたい、英: regular icosahedron）は立体の名称の1つ。空間を正三角形20枚で囲んだ凸多面体。3次元空間で最大の面数を持つ正多面体である。

正多面体のひとつである正十二面体の頂点周りを面の中心まで切頂することによって得られる（双対関係）。

また、正六面体や正十二面体に対する捩じり切り操作と同様の操作を正四面体に対して行うことでも得られる^[1]。

性質[編集]

正二十面体サイコロ

正反五角柱の両底面に正五角錐を貼り付けた形である。よって、正二十面体を双五角錐反柱 (Gyroelongated pentagonal bipyramid) と呼ぶ場合がある。
向かい合う面は平行である。
展開図の数は43,380種類。
面の数は20、辺の数は30、頂点の数は12。
頂点形状は正五角形であり、5本の辺と5枚の正三角形が集まる。
正十二面体と双対である。

計量[編集]

一辺の長さをaとすると、

面の面積	$A={1 \over 4}{\sqrt {3}}a^{2}$
表面積	$S=20A=5{\sqrt {3}}a^{2}$
体積	$V={\frac {1}{3}}Sr={15+5{\sqrt {5}} \over 12}a^{3}$
最長対角線の長さ	$d={{\sqrt {10+2{\sqrt {5}}}} \over 2}a$
外接球半径	$R={\frac {d}{2}}={{\sqrt {10+2{\sqrt {5}}}} \over 4}a$
内接球半径	$r={3{\sqrt {3}}+{\sqrt {15}} \over 12}a$

頂点、辺、面の座標[編集]

以下は、標準的な座標の取り方の一つである。ここで $\phi$ は黄金比 ${\frac {1+{\sqrt {5}}}{2}}$ 、 $\epsilon _{1},\epsilon _{2},\epsilon _{3}=\pm 1$ である。

12個の頂点（原点からの距離 ${\sqrt {\phi +2}}$ ）の座標

$(0,\epsilon _{2},\epsilon _{3}\phi )$ のxyz座標を偶置換した 12個

30個の辺（長さ $2$ ）の、両端点および中心の座標

両端点 $(0,\epsilon _{2},\epsilon _{3}\phi )$ と $(\epsilon _{1},\epsilon _{2}\phi ,0)$ 、中心 ${\frac {1}{2}}(\epsilon _{1},\epsilon _{2}\phi ^{2},\epsilon _{3}\phi )$ のxyz座標を偶置換した 24個
両端点 $(0,1,\epsilon _{3}\phi )$ と $(0,-1,\epsilon _{3}\phi )$ 、中心 $(0,0,\epsilon _{3}\phi )$ のxyz座標を偶置換した 6個

20個の面の、外側から見て反時計回りの頂点列および中心の座標

頂点 $(0,\epsilon _{2},\epsilon _{1}\epsilon _{2}\phi ),(\epsilon _{1}\phi ,0,\epsilon _{1}\epsilon _{2}),(\epsilon _{1},\epsilon _{2}\phi ,0)$ の4個
頂点 $(0,\epsilon _{2},-\epsilon _{1}\epsilon _{2}\phi ),(\epsilon _{1},\epsilon _{2}\phi ,0),(\epsilon _{1}\phi ,0,-\epsilon _{1}\epsilon _{2})$ の4個
頂点 $(0,\epsilon _{2},\epsilon _{3}\phi )$ , $(0,-\epsilon _{2},\epsilon _{3}\phi )$ , $(\epsilon _{2}\epsilon _{3}\phi ,0,\epsilon _{3})$ のxyz座標を偶置換した 12個

対称性[編集]

完全正二十面体的対称性（英語版）には（この球面で水色の大円として見えている）15枚の鏡映平面があり、それらはπ/5、π/3、π/2の角度で会し、球面を120の三角形の基本領域（英語版）（黄）に分かつ。また、6本の5回回転軸（英：5-fold axes）（青）、10本の3回回転軸（赤）、15本の2回回転軸（赤紫）がある。正二十面体の頂点は5回回転軸上の点に存在する。

詳細は「en:Icosahedral symmetry」を参照

正二十面体の回転対称群（英語版）は5文字の交代群 $A_{5}$ に同型である。位数は60。この非可換単純群は5文字の対称群 $S_{5}$ の唯一の非自明な正規部分群である。一般の五次方程式のガロア群は5文字の対称群に同型であり、そしてこの正規部分群が単純で非可換なので、一般の五次方程式は冪根による解を有しない。アーベル‐ルフィニの定理の証明はこの単純な事実を用いる。そしてフェリックス・クラインは正二十面体的対称性（英語版）の理論を利用して一般の五次方程式の解析的解法を導く本を書いた (Klein 1888)。詳しい歴史ならびに関係する7文字と11文字の対称性については正二十面体的対称性#関連する幾何学的性質（英語版）を見よ。