四角錐


四角錐(しかくすい、英: Square pyramid)とは、底面が四角形の錐体である。四角形は多角形なので、四角錐は角錐でもある。
種類[編集]
- 長方錐(ちょうほうすい) - 底面が長方形である四角錐。
- 方錐(ほうすい) - 底面が正方形である四角錐。
- 正四角錐(せいしかくすい) - 直錐である(頭頂点から底面への垂線が底面の重心を通る)方錐。いわゆる「ピラミッド型」である。しばしば斜錐の存在を考慮せず、方錐と正四角錐を同義と説明することがある。
- 斜方錐(しゃほうすい) - 斜錐である方錐。(右下図)
側面が正三角形である正四角錐は、ジョンソンの立体の1番目である。ジョンソンの立体となる角錐は四角錐と五角錐のみである。(三角錐は正四面体、六角錐は正三角形だと重なってしまう。)
性質[編集]

長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。直錐の場合、側面積 S は
となる。
任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。
ここで は、この正四角錐を平面 Z = 1 で切断したときの、断面の境界(正方形)の一辺の長さになる。
ジョンソンの立体となる正四角錐[編集]
| 正四角錐 (ジョンソンの立体) | |
|---|---|
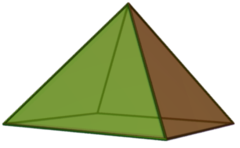 | |
| 種別 |
ジョンソンの立体、角錐 J92 – J1 – J2 |
| 面数 | 5 |
| 面形状 |
正三角形: 4 正方形: 1 |
| 辺数 | 8 |
| 頂点数 | 5 |
| 頂点形状 |
1(34) 4(32, 4) |
| 対称群 | C4v |
| 双対多面体 | 自己双対 |
| 特性 | 凸集合 |
性質[編集]
- 高さ: 一辺をとすると
- 表面積: 一辺をとすると
- 体積: 一辺をとすると
近縁な立体[編集]
関連項目[編集]
外部リンク[編集]
- Weisstein, Eric W. "Square Pyramid". mathworld.wolfram.com (英語).

















