連続写像

数学において、関数または写像 $f$ が、定義域のある点 $a$ において連続（れんぞく、英: continuous）であるとは、 $f$ が $a$ において極限を保つこと、平たく言えば、 $f$ の入力 $x$ を $a$ に「限りなく近づける」ことで、その近づけ方によらず、出力 $f (x)$ をも $f (a)$ に「限りなく近づける」ことができるということである。特に定義域の全ての点において連続であるとき、 $f$ は連続関数（れんぞくかんすう、英: continuous function）または連続写像（れんぞくしゃぞう）という。連続でないことは不連続（ふれんぞく、英: discontinuous）という。

連続性は多項式関数や指数関数といった多くの初等関数が備える性質であり、実数値関数では連結集合^{[注 1]}の上で中間値の定理、コンパクト集合^{[注 2]}の上で最大値最小値定理が成り立つほか、微分可能であるための必要条件や積分可能であるための十分条件でもあるなど、解析学的に重要な性質を伴う。

連続性は位相空間論において一般化され、近傍系や開集合系などの位相的構造を逆像で保つこととして定義され（後述）、この意味で連続写像は位相的構造についての準同型である。そのため、位相空間の間の写像が、双方向に位相的構造を保つ写像、つまり同相写像であることは、逆も連続な全単射連続写像であることと同値である。さらに、連続写像は位相空間の圏における射となる。また、連続性はホモトピーの定義などを通じて位相幾何学の土台をなす。

実関数の連続性

実関数、すなわち定義域と値域がともに実数直線上にある関数 $f (x)$ が $x = a$ を含む区間で定義されているとき、座標平面上にそのグラフを描くことができるが、 $a$ における連続性とは、『数直線上の左から $x = a$ に近づいたときの極限値と、数直線上の右から $x = a$ に近づいたときの極限値が一致して、しかも $f (a)$ に等しいこと』^[1]であり、関数の極限を用いて以下の等式で定義される^[1]^{[注 3]}。

\lim _{x\to a}f(x)=f(a)

これはε-δ論法によって次のように言い換えることができる。

任意の正の実数

ε

について、適切に正の実数

δ

をとることで、

f

の定義域に含まれて

| x - a | < δ

を満たす全ての

x \neq a

について

| f (x) - f (a)| < ε

が成り立つ。

これはつまり、どれだけ小さな正の実数 $ε$ に対しても「 $a$ との誤差が $δ$ 未満である $x \neq a$ を持ってくれば、 $f (a)$ との誤差が $ε$ 未満であることが保証された $f (x)$ を得られる」ような正の実数 $δ$ が存在するということを意味する^[3]。なお、 $x \neq a$ の条件は無くてもよい^{[注 4]}。

関数 $f (x)$ が定義域上のすべての点において連続であるとき、これを連続関数と呼ぶ^[1]。

以下に挙げるように、連続関数を組み合わせてできる様々な関数が再び連続関数になることが知られている^[6]^[7]。

関数 f(x) と g(x) がいずれも a において連続であるとき、以下の関数もまた a において連続である。これは一般の位相空間上で定義される実数値関数においても成立する^[8]。
- $k f (x) + l g (x)$ （ $k$ と $l$ は実数）
- $f (x) \cdot g (x)$
- $f (x) / g (x)$ （ただし $g (a) \neq 0$ ）
関数 $f (x)$ が $a$ において連続で、 $g (x)$ が $b = f (a)$ において連続であるとき、合成関数 $(g \circ f)(x) = g (f (x))$ もまた $a$ において連続である。これは位相空間の間の写像について一般に成立する^[9]。つまり、連続写像の全体は合成について閉じている。

例

実数上で定義された二次関数 $f (x) = x 2$ は任意の実数 $a$ において連続である。実際、任意の $ε > 0$ に対して、 $δ = \sqrt a 2 + ε - \sqrt a 2 > 0$ とすることで、 $| x - a | < δ$ を満たす $x$ について、 $| x 2 - a 2 | < ε$ が成り立つ^{[注 5]}。
床関数 $f (x) = ⌊ x ⌋$ は点 $a = 0$ において不連続である。実際、任意の $δ > 0$ に対して、 $- δ < x < 0$ を満たす $x$ について $| ⌊ x ⌋ - 0| \geq 1$ であり、 $ε \leq 1$ に対して「 $| x - a | < δ$ ならば $| f (x) - f (a)| < ε$ である」ような $δ$ が存在しない。

距離空間の間の写像の連続性

一般の距離空間 $(X, d X)$ と $(Y, d Y)$ の間の写像 $f : X \to Y$ についても、 $a \in X$ における連続性の定義は

\lim _{x\to a}f(x)=f(a)

で与えられる。

これもまたε-δ論法によって、

任意の正の実数

ε

について適切な正の実数

δ

をとることで、

d X (x, a) < δ

を満たす全ての

x

について

d Y (f (x), f (a)) < ε

が成り立つ

と言い換えることができる^[10]。

また、点 $p$ の $ε$ -近傍 $B ε (p) = {q | d (q, p) < ε}$ の概念を用いることで、

任意の正の実数

ε

について適切な正の実数

δ

をとることで、

a

の

δ

-近傍に含まれる全ての

x

について

f (x)

は

f (a)

の

ε

-近傍に含まれる

とも言えて^{[注 6]}、 $x \in A \to f (x) \in B \Leftrightarrow f (A) \subset B \Leftrightarrow A \subset f -1 (B)$ であることから、一階述語論理で

\forall \varepsilon >0\;\exists \delta >0\;{\bigl [}f(B_{\delta }(a))\subset B_{\varepsilon }(f(a)){\bigr ]}

（

f (a)

の任意の

ε

-近傍は

a

のある

δ

-近傍の像を包む）

あるいは

\forall \varepsilon >0\;\exists \delta >0\;{\bigl [}B_{\delta }(a)\subset f^{-1}(B_{\varepsilon }(f(a))){\bigr ]}

（

f (a)

の任意の

ε

-近傍の逆像は

a

のある

δ

-近傍を包む）

と表すこともできる^[11]。

さらに、点 $p$ の近傍の全体 $N (p) = {V | \existsε > 0 [B ε (p) \subset V]}$ を用いて、ε や $δ$ が現れず距離に明示的に依存しない形に書き直すことができる。 $f (a)$ の任意の近傍 $V$ はある $ε$ -近傍を包んでいるので、それに対応した $a$ のある $δ$ -近傍を近傍 $W$ として持ってくるのである。その結果、

\forall V\in {\mathcal {N}}(f(a))\;\exists W\in {\mathcal {N}}(a)\;{\bigl [}f(W)\subset V{\bigr ]}

（

f (a)

の任意の近傍

V

は

a

のある近傍

W

の像を包む）

あるいは

\forall V\in {\mathcal {N}}(f(a))\;\exists W\in {\mathcal {N}}(a)\;{\bigl [}W\subset f^{-1}(V){\bigr ]}

（

f (a)

の任意の近傍

V

の逆像は

a

のある近傍

W

を包む）

とあらわすことができる。特に後者はより短く

\forall V\in {\mathcal {N}}(f(a))\;{\bigl [}f^{-1}(V)\in {\mathcal {N}}(a){\bigr ]}

（

f (a)

の任意の近傍

V

の逆像は

a

の近傍である）

と表すこともできる。

位相空間の間の写像の連続性

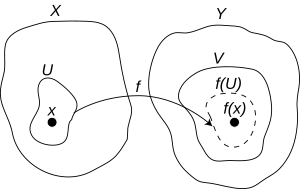
前節の通り、距離空間の間の写像の連続性は、近傍を用いて距離に明示的に依存せずに表すことができた。これを位相が定める近傍系に適用することで、一般の位相空間 $(X, 𝒪 X)$ と $(Y, 𝒪 Y)$ の間の写像 $f : X \to Y$ について $a \in X$ における連続性は、

\forall V\in {\mathcal {N}}(f(a))\;{\bigl [}f^{-1}(V)\in {\mathcal {N}}(a){\bigr ]}

で定義される^[12]。これは距離空間のときと同じように

\forall V\in {\mathcal {N}}(f(a))\;\exists W\in {\mathcal {N}}(a)\;{\bigl [}f(W)\subset V{\bigr ]}

あるいは

\forall V\in {\mathcal {N}}(f(a))\;\exists W\in {\mathcal {N}}(a)\;{\bigl [}W\subset f^{-1}(V){\bigr ]}

と書いても同じである。写像 $f$ が $X$ のすべての点において連続であるならば、 $f$ を連続写像という^[12]。

連続写像は近傍系以外の位相的構造を用いて定義することもできる。位相空間 $(X, 𝒪 X)$ と $(Y, 𝒪 Y)$ の間の写像 $f : X \to Y$ について、以下の3条件は互いに同値である^[13]。

$Y$ の任意の開集合 $O$ に対して、その逆像 $f -1 (O)$ が $X$ の開集合である^{[注 7]}。
$Y$ の任意の閉集合 $F$ に対して、その逆像 $f -1 (F)$ が $X$ の閉集合である。
$X$ の任意の点 $x$ について、 $f (x)$ の任意の近傍 $V$ の逆像 $f -1 (V)$ が $x$ の近傍である^{[注 8]}。

このことから、開集合や閉集合を用いて連続写像を定義することもできる。特に、位相を開集合によって定義する流儀が多いことに伴い、開集合を用いた定義が採用されることが多い。

他に、各部分集合 $A \subseteq X$ にその閉包を割り当てる閉包作用素（英語版） $cl$ や、開核を割り当てる開核作用素 $int$ も位相を定めるが、これらを用いると、位相空間の間の写像

f\colon (X,\mathrm {cl} )\to (X',\mathrm {cl} ')

が上記の意味で連続となるための必要十分条件は、任意の部分集合 $A \subseteq X$ に対して

f(\mathrm {cl} (A))\subseteq \mathrm {cl} '(f(A))

が成り立つことである。これはつまり、 $X$ の与えられた元 $x$ が任意の部分集合 $A$ の閉包に属す限りにおいて、 $f (x)$ は必ず $f (A)$ の閉包に属すことを言っている。これはまた $X'$ の任意の部分集合 $A'$ に対して

f^{-1}(\mathrm {cl} '(A'))\supseteq \mathrm {cl} (f^{-1}(A'))

を満足することを課すのと同値である。あるいは開核作用素を用いて、写像

f\colon (X,\mathrm {int} )\to (X',\mathrm {int} ')

が連続となる必要十分条件を、任意の部分集合 $A \subseteq X$ に対し

f^{-1}(\mathrm {int} '(A))\subseteq \mathrm {int} (f^{-1}(A))

が満足されることと述べることもできる。

点列および有向点族を用いた定義

この記事の冒頭では、「（点を）限りなく近づける」という喩えを用いて、連続写像を極限を保つ写像だと説明した。距離空間上で点の極限を厳密に議論するためにはε-N論法で定義されるような列の極限がよく用いられる。しかし、これは一般の位相空間に対して連続性を特徴づけるには（単にε-N論法の $ε$ -近傍を一般の近傍に書き換えるだけでは）不十分であり、極限の概念を点列より広い概念に拡張する必要がある。

「列の極限を保つ」写像は点列連続（英: sequentially continuous）と呼ばれる。すなわち、写像 $f : X \to Y$ が点列連続であるとは、 $X$ 内の点列 $(x n)$ が極限点 $a$ に収束するならば像の列 $(f (x n))$ が $f (a)$ に収束することである。

任意の連続写像は点列連続である。さらに、 $X$ が第一可算空間の商位相空間ならば、逆もまた成立して任意の点列連続写像は連続であり、このような空間は列型空間と呼ばれる。特に、任意の距離空間は自然数 $N$ についての $.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1⁄N$ -近傍の全体が基本近傍系をなすことから、第一可算公理を満たして列型空間である。

列型空間でない位相空間では点列連続性が連続性よりも真に弱い。そのような空間でも極限によって連続性を扱えるようにするために点列の概念を拡張したものが有向点族（有向点列、ネット）である。これは可算な全順序集合である自然数 N の代わりに、適当な有向集合 $Λ$ を添字集合とするような点の族である。有向点族 $(x λ) λ \in Λ$ が $a$ に収束するとは、 $a$ の任意の近傍 $V$ に対しても、適当な $λ 0 \in Λ$ が存在して、 $λ 0 \leq λ$ を満たす全ての $λ \in Λ$ について $x λ \in V$ であることとして定義される^[14]。特に、ハウスドルフ空間では収束する有向点族の極限はただ一点である^{[注 9]}。

この有向点族の極限を用いることで、写像の連続性を表すことができるようになる。というのも、 $a \in X$ に収束する任意の有向点族 $(x λ) λ \in Λ$ について $(f (x λ)) λ \in Λ$ が必ず $f (a)$ に収束することが、 $a$ において $f : X \to Y$ が連続であるための必要十分条件となる^[14]^{[注 10]}からである。これにより、連続写像を「有向点族の極限を保つ」写像として定義することができる。

性質

二つの写像 $f : X \to Y, g : Y \to Z$ が連続ならば、それらの合成 $g \circ f : X \to Z$ もそうである。また $f : X \to Y$ が連続のとき、

$X$ がコンパクトならば $f (X)$ もコンパクト^[15]；
$X$ が連結ならば $f (X)$ も連結^[16]；
$X$ が弧状連結ならば $f (X)$ も弧状連結；
$X$ がリンデレフならば $f (X)$ もリンデレフ；
$X$ が可分ならば $f (X)$ も可分
$X$ がハウスドルフであっても $f (X)$ がハウスドルフであるとは限らない；

である。

一つ固定した空間 $X$ 上に入れることのできる位相の全体には半順序を入れることができて、位相 $τ 1$ が別の位相 $τ 2$ よりも粗い（英語版） ( $τ 1 \subseteq τ 2$ ) とは、 $τ 1$ に関する任意の開集合が、必ず $τ 2$ に関する開集合ともなるときに言うのであった。さてこのとき、恒等写像

id X : (X, τ 2) \to (X, τ 1)

が連続となる必要十分条件は $τ 1 \subseteq τ 2$ が成り立つことである。より一般に、連続写像

(X,\tau _{X})\to (Y,\tau _{Y})

に対し、位相 $τ Y$ をより粗い位相に取り換えても、また $τ X$ をより細かい位相に取り換えても、連続性は保たれる。

定義域 $X$ に離散位相を入れるとき、任意の写像 $f : X \to Y$ は任意の位相空間 $Y$ を終域として連続である。
終域 $Y$ に密着位相を入れるとき、任意の写像 $f : X \to Y$ は任意の位相空間 $X$ を定義域として連続である。
定義域が密着空間で終域が T₀-空間ならば、定値写像のみが連続になる。
連続性は局所的な性質（英語版）である。

同相写像

→詳細は「位相同型」を参照

連続写像は開集合の逆像が開集合となり、閉集合の逆像が閉集合となる写像であったが、それと対照的に「開集合の像が開集合となる」写像と「閉集合の像が閉集合となる」写像は、それぞれ開写像と閉写像と呼ばれる。つまり、開写像あるいは閉写像が逆写像を持てばそれは連続であり、連続写像が逆を持てばその逆写像は開かつ閉写像である^{[注 11]}。このことから、位相空間の間の写像について以下は全て同値である。

両連続写像（逆も連続な連続写像^{[注 12]}）
全単射な連続開写像
全単射な連続閉写像
逆も開である開写像
逆も閉である閉写像
逆が閉である開写像

このような写像は開集合系や近傍系といった位相的構造を双方向に保つ^{[注 13]}ため、位相同型写像、あるいは同相写像と呼ばれる。また、同相写像 $f : X \to Y$ が存在するとき、 $X$ と $Y$ は互いに位相同型である、あるいは同相であるという^[18]。

連続写像の定める位相

位相空間 $X$ から（特に位相を考えない）集合 $S$ への写像

f\colon X\to S

が与えられたとき、 $S$ 上の終位相（英語版）は、 $S$ の部分集合 $A$ が開集合であるということを、 $f -1 (A)$ が $X$ の開集合であることと定めることにより定義される。 $S$ に予め位相が定められていたとき、 $f$ がその位相に関して連続となる必要十分条件は、もとの位相が $S$ 上の終位相よりも粗いことである。従って、終位相は $S$ 上の $f$ を連続にする最も細かい位相となる。 $f$ が全射のとき、終位相は $f$ の定める同値関係のもとでの商位相と自然に同一視される。

これと双対的に、集合 $S$ から位相空間への写像 $f$ に対し、 $S$ 上の始位相（英語版）は、 $S$ の部分集合 $A$ が開集合であることを、 $f (A)$ が $X$ の開集合となることと定めることによって定義される。 $S$ にもともと位相が入っているとき、 $f$ がその位相に関して連続となる必要十分条件は、その位相が $S$ 上の始位相よりも細かいことである。従って、始位相は $S$ 上の位相として $f$ を連続にする最も粗い位相となる。 $f$ が単射のとき $S$ を $X$ の部分集合と同一視すれば、 $S$ 上の始位相は $X$ から定まる部分空間としての位相と自然に同一視される。

より一般に、集合 $S$ が与えられたとき、任意の位相空間 $X$ への連続写像 $S \to X$ 全体の成す集合を特定することにより、 $S$ に位相が定まる。双対的に同じことが $X \to S$ に対しても考えられる。これは普遍性の一例である。

脚注

[脚注の使い方]

注釈

^ 実関数では単一の区間
^ ユークリッド空間上の関数では有界閉集合
^ 杉浦^[2]も同じ等式で定義しているが、より一般にユークリッド空間について述べていることと、極限の定義が一般的な定義と僅かに異なる（同値ではない）ことに注意を要する。この記事での意味の等式に最も近い表現は命題6.5の d) である。
^ 一般に関数の極限を扱う際には $x \neq a$ であること、あるいは同じことだが、絶対値の条件が $0 < | x - a | < δ$ と正値をとること^[4]が要求される。これは必ずしも $f (a)$ が極限値 $A$ と等しいとは限らず、そのような場合に $| f (a) - A | < ε$ が成り立たない $ε$ が存在して極限の議論の妨げになるためであった。しかし、連続関数は $A = f (a)$ となるべきものであり、どのような正の実数 $ε$ についても $| f (a) - f (a)| = 0 < ε$ が自明に成り立つので、 $x = a$ を含めても条件が厳しくなることはない。そのため、 $f (x)$ の連続性は、「任意の正の実数 $ε$ について適切な正の実数 $δ$ をとることで、 $f$ の定義域に含まれて $| x - a | < δ$ を満たす全ての $x$ について $| f (x) - f (a)| < ε$ が成り立つ」ことだとも言える^[5]。
^ ${\begin{aligned}\left|x^{2}-a^{2}\right|&=|x-a|\cdot |x+a|\leq |x-a|\cdot (|x-a|+2|a|)\\&<\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)\left[\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)+2{\sqrt {a^{2}}}\right]\\&=\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)\left({\sqrt {a^{2}+\varepsilon }}+{\sqrt {a^{2}}}\right)\\&=\left(a^{2}+\varepsilon \right)-a^{2}=\varepsilon \end{aligned}}$
^ ここで、 $a$ の $δ$ -近傍は $(X, d X)$ におけるもの、 $f (a)$ の $ε$ -近傍は $(Y, d Y)$ におけるものであることには注意が必要である。
^ 開集合全てでなく準開基に限ったとしても同値である。
^ 全近傍系の代わりに基本近傍系や開近傍系に限ったとしても同値である。例えば、距離空間においては各点の $ε$ -近傍の全体が基本近傍系となるので、ε-δ論法による定義は基本近傍系によるものだということもできる。
^ これは逆も真であり、ハウスドルフ空間の特徴づけになっている。
^ 特に $Y$ がハウスドルフ空間であるときは、 $x$ を $a$ に限りなく近づけるときの $f$ の極限が $f (a)$ であることだと言える。
^ 逆写像を持たない、つまり全単射でない写像においては、開写像と閉写像は一致するとは限らない。例えば、実数を終域とする定値写像は閉写像だが開写像ではない。ちなみに定値写像は、終域のいかなる部分集合も逆像は定義域全体か空集合のどちらかであり、どちらも開かつ閉集合であるから、必ず連続写像である。
^ 全単射である連続写像に対して、その逆写像は必ずしも連続でない。例えば、ある2点集合を共通の台集合とする離散空間と密着空間を考えると、台集合上の恒等写像は離散空間から密着空間への全単射連続写像となるが、逆は連続でない。ただし、定義域がコンパクト空間で終域がハウスドルフ空間ならば、連続全単射は閉写像でもあるので同相である^[17]。
^ 当然、閉集合系や開核、閉包も保つ

出典

^ ^a ^b ^c 加藤 2019, p. 71.
^ 杉浦 1985, 第I章 §6.
^ 杉浦 1985, 第I章 §6 命題6.5 d).
^ 加藤 2019, p. 62.
^ 杉浦 1985, 第I章 §6 命題6.5 c).
^ 加藤 2019, pp. 72–74.
^ 杉浦 1985, pp. 57–59.
^ 松坂 1968, pp. 178–182.
^ 松坂 1968, pp. 185.
^ 松坂 1968, p. 240.
^ 松坂 1968, pp. 240–241.
^ ^a ^b 松坂 1968, p. 178.
^ 松坂 1968, pp. 175–176.
^ ^a ^b 松坂 1968, p. 246.
^ 松坂 1968, p. 212.
^ 松坂 1968, p. 196.
^ 松坂 1968, pp. 216.
^ 松坂 1968, pp. 182–185.

文献

加藤文元『大学教養微分積分』数研出版〈数研講座シリーズ〉、2019年11月1日。ISBN 978-4-410-15229-0。
杉浦光夫『解析入門I』東京大学出版会〈基礎数学〉、1985年4月25日。ISBN 4-13-062005-3。
松坂和夫『集合・位相入門』岩波書店〈松坂和夫数学入門シリーズ〉、1968年6月10日。ISBN 978-4-00-029871-1。
Boto von Querenburg (2001), Mengentheoretische Topologie, Springer-Lehrbuch (ドイツ語) (3., neu bearbeitete und erweiterte ed.), Berlin [u. a.]: Springer-Verlag, ISBN 3-540-67790-9。
Friedrich Hirzebruch / Winfried Scharlau (1971), Einführung in die Funktionalanalysis, Reihe "B. I.-Hochschultaschenbücher", Band Nr (ドイツ語), vol. 296, Mannheim [u. a.]: Bibliographisches Institut, ISBN 3-411-00296-4。 MR0463864
Horst Schubert (1975), Topologie. Eine Einführung, Mathematische Leitfäden (ドイツ語) (4. ed.), Stuttgart: B. G. Teubner Verlag, ISBN 3-519-12200-6。 MR0423277

外部リンク

Topology without tears von Sidney A. Morris: Buch zur Topologie zum kostenfreien Download（英語）

[1] 実関数では単一の区間

[2] ユークリッド空間上の関数では有界閉集合

[5] 杉浦^[2]も同じ等式で定義しているが、より一般にユークリッド空間について述べていることと、極限の定義が一般的な定義と僅かに異なる（同値ではない）ことに注意を要する。この記事での意味の等式に最も近い表現は命題6.5の d) である。

[9] 一般に関数の極限を扱う際には $x \neq a$ であること、あるいは同じことだが、絶対値の条件が $0 < | x - a | < δ$ と正値をとること^[4]が要求される。これは必ずしも $f (a)$ が極限値 $A$ と等しいとは限らず、そのような場合に $| f (a) - A | < ε$ が成り立たない $ε$ が存在して極限の議論の妨げになるためであった。しかし、連続関数は $A = f (a)$ となるべきものであり、どのような正の実数 $ε$ についても $| f (a) - f (a)| = 0 < ε$ が自明に成り立つので、 $x = a$ を含めても条件が厳しくなることはない。そのため、 $f (x)$ の連続性は、「任意の正の実数 $ε$ について適切な正の実数 $δ$ をとることで、 $f$ の定義域に含まれて $| x - a | < δ$ を満たす全ての $x$ について $| f (x) - f (a)| < ε$ が成り立つ」ことだとも言える^[5]。

[14] ${\begin{aligned}\left|x^{2}-a^{2}\right|&=|x-a|\cdot |x+a|\leq |x-a|\cdot (|x-a|+2|a|)\\&<\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)\left[\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)+2{\sqrt {a^{2}}}\right]\\&=\left({\sqrt {a^{2}+\varepsilon }}-{\sqrt {a^{2}}}\right)\left({\sqrt {a^{2}+\varepsilon }}+{\sqrt {a^{2}}}\right)\\&=\left(a^{2}+\varepsilon \right)-a^{2}=\varepsilon \end{aligned}}$

[16] ここで、 $a$ の $δ$ -近傍は $(X, d X)$ におけるもの、 $f (a)$ の $ε$ -近傍は $(Y, d Y)$ におけるものであることには注意が必要である。

[20] 開集合全てでなく準開基に限ったとしても同値である。

[21] 全近傍系の代わりに基本近傍系や開近傍系に限ったとしても同値である。例えば、距離空間においては各点の $ε$ -近傍の全体が基本近傍系となるので、ε-δ論法による定義は基本近傍系によるものだということもできる。

[23] これは逆も真であり、ハウスドルフ空間の特徴づけになっている。

[24] 特に $Y$ がハウスドルフ空間であるときは、 $x$ を $a$ に限りなく近づけるときの $f$ の極限が $f (a)$ であることだと言える。

[27] 逆写像を持たない、つまり全単射でない写像においては、開写像と閉写像は一致するとは限らない。例えば、実数を終域とする定値写像は閉写像だが開写像ではない。ちなみに定値写像は、終域のいかなる部分集合も逆像は定義域全体か空集合のどちらかであり、どちらも開かつ閉集合であるから、必ず連続写像である。

[29] 全単射である連続写像に対して、その逆写像は必ずしも連続でない。例えば、ある2点集合を共通の台集合とする離散空間と密着空間を考えると、台集合上の恒等写像は離散空間から密着空間への全単射連続写像となるが、逆は連続でない。ただし、定義域がコンパクト空間で終域がハウスドルフ空間ならば、連続全単射は閉写像でもあるので同相である^[17]。

[30] 当然、閉集合系や開核、閉包も保つ

[FOOTNOTE加藤201971-3] 加藤 2019, p. 71.

[FOOTNOTE杉浦1985第I章_§6-4] 杉浦 1985, 第I章 §6.

[FOOTNOTE杉浦1985第I章_§6_命題6.5_d)-6] 杉浦 1985, 第I章 §6 命題6.5 d).

[FOOTNOTE加藤201962-7] 加藤 2019, p. 62.

[FOOTNOTE杉浦1985第I章_§6_命題6.5_c)-8] 杉浦 1985, 第I章 §6 命題6.5 c).

[FOOTNOTE加藤201972–74-10] 加藤 2019, pp. 72–74.

[FOOTNOTE杉浦198557–59-11] 杉浦 1985, pp. 57–59.

[FOOTNOTE松坂1968178–182-12] 松坂 1968, pp. 178–182.

[FOOTNOTE松坂1968185-13] 松坂 1968, pp. 185.

[FOOTNOTE松坂1968240-15] 松坂 1968, p. 240.

[FOOTNOTE松坂1968240–241-17] 松坂 1968, pp. 240–241.

[FOOTNOTE松坂1968178-18] 松坂 1968, p. 178.

[FOOTNOTE松坂1968175–176-19] 松坂 1968, pp. 175–176.

[FOOTNOTE松坂1968246-22] 松坂 1968, p. 246.

[FOOTNOTE松坂1968212-25] 松坂 1968, p. 212.

[FOOTNOTE松坂1968196-26] 松坂 1968, p. 196.

[FOOTNOTE松坂1968216-28] 松坂 1968, pp. 216.

[FOOTNOTE松坂1968182–185-31] 松坂 1968, pp. 182–185.

[注 1]

[注 2]

[1]

[注 3]

[3]

[注 4]

[6]

[7]

[8]

[9]

[注 5]

[10]

[注 6]

[11]

[12]

[13]

[注 7]

[注 8]

[14]

[注 9]

[注 10]

[15]

[16]

[注 11]

[注 12]

[注 13]

[18]

[2]

[4]

[5]

[17]

表話編歴解析学の主要なトピックス
微分積分学: 積分法微分法微分方程式 (常 - 偏) 基本定理変分法ベクトル解析テンソル解析積分一覧導関数一覧（英語版）
実解析複素解析関数解析フーリエ解析調和解析測度論表現論関数連続関数特殊関数極限級数無限
ポータル・カテゴリ

表話編歴微分積分学
Precalculus	二項定理凹関数連続関数階乗有限差分自由変数と束縛変数基本定理関数のグラフ線型関数平均値の定理ラジアンロルの定理割線傾き接線
極限	不定形（英語版）関数の極限片側極限数列の極限数列の加速法近似のオーダー（英語版） ε-δ論法
微分法	連鎖律導関数微分微分方程式微分作用素陰関数微分逆関数の微分（英語版）ロピタルの定理ライプニッツ則対数微分平均値の定理ニュートン法記法ライプニッツの記法ニュートンの記法レギオモンタヌスの問題相対変化率（英語版）基本法則線型性（英語版）積商冪函数（英語版）停留点極値の判定（英語版）最大値の定理極値テイラーの定理
積分法	逆微分弧長積分定数積分記号下の微分（英語版）微分積分学の基本定理正割の立方の積分（英語版）正割関数の積分（英語版）半角正接置換法（英語版）積分における部分分数（英語版）二次有理式の積分（英語版）円周率が22/7より小さいことの証明基本法則線型性（英語版）部分積分置換積分台形公式三角函数置換法（英語版）
ベクトル解析	回転方向微分発散発散定理勾配勾配定理（英語版）グリーンの定理ラプラシアンストークスの定理
多変数微分積分学	曲率 Disc integration（英語版）発散定理外微分ガブリエルのホルン幾何解析（英語版）ヘッセ行列ヤコビ行列と行列式線積分 Matrix calculus 多重積分偏微分バウムクーヘン積分面積分テンソル解析体積分
級数	アーベルの判定法（英語版）交代交代級数判定法（英語版）算術幾何数列二項コーシーの凝集判定法比較判定法ディリクレの判定法オイラー–マクローリンの公式フーリエ幾何超幾何 q超幾何調和無限積分判定法極限比較判定法（英語版）マクローリン冪比判定法冪根判定法テイラー項判定法（英語版）
特殊関数と数学定数	ベルヌーイ数ネイピア数オイラー定数指数関数自然対数ガンマ関数スターリングの近似楕円関数
歴史（英語版）	擬等式（英語版）ブルック・テイラーコリン・マクローリン代数の一般性（英語版）ゴットフリート・ヴィルヘルム・ライプニッツ無限小無限小解析（英語版）アイザック・ニュートン連続の法則（英語版）レオンハルト・オイラー『流率法』 (流率（英語版）) 『方法（英語版）』
一覧	微分法則（英語版）指数関数の原始関数双曲線関数の原始関数逆双曲線関数の原始関数逆三角関数の原始関数無理関数の原始関数対数関数の原始関数有理関数の原始関数三角関数の原始関数極限数学記号原始関数
カテゴリ

表話編歴位相幾何学・トポロジー
分野	一般（点集合）代数的組合せ論的（英語版）連続体微分幾何学的ホモロジーコホモロジー集合論的（英語版）
主要概念	開集合 / 閉集合連続性空間コンパクトハウスドルフ距離一様ホモトピーホモトピー群基本群単体複体 CW複体完全列ホモロジー代数 K理論
Glossary（英語版） Lists トピックス（英語版）一般（英語版）代数的（英語版）幾何学的（英語版）出版物（英語版）

実関数の連続性

距離空間の間の写像の連続性

位相空間の間の写像の連続性

点列および有向点族を用いた定義

性質

同相写像

連続写像の定める位相

脚注

注釈

出典

文献

関連項目

外部リンク