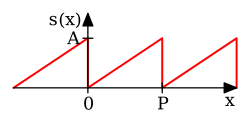方形波 (青線)とフーリエ級数による近似(赤線)。最初の4項まで。フーリエ級数 (フーリエきゅうすう、英語 : Fourier series )とは、複雑な周期関数 や周期信号を単純な形の周期性をもつ関数の無限和(級数 )によって表したものである。フーリエ級数は、フランスの数学者ジョゼフ・フーリエ によって金属 板の中での熱伝導 に関する研究の中で導入された。
熱伝導方程式 は、偏微分方程式 として表される。フーリエの研究の前までには、一般的な形での熱伝導方程式の解法は知られておらず、熱源が単純な形である場合、例えば正弦波 などの場合の特別な解しかえられていなかった。この特別な解は現在では固有解と呼ばれる。フーリエの発想は、複雑な形をした熱源をサイン波、コサイン波の線型結合 として考え、解を固有解の和として表すものであった。
この重ね合わせがフーリエ級数と呼ばれる。
最初の動機は熱伝導方程式を解くことであったが、数学や物理の他の問題にも同様のテクニックが使えることが分かり様々な分野に応用されている。
フーリエ級数は、電気工学 、振動 の解析、音響学 、光学 、信号処理 、量子力学 および経済学 [1]
フーリエ級数は、関数に対して定義されるフーリエ係数を用いて
a
0
2
+
∑
k
=
1
∞
(
a
k
cos
k
x
+
b
k
sin
k
x
)
{\displaystyle {\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }(a_{k}\cos kx+b_{k}\sin kx)}
の形に表される三角級数のことである。熱方程式 を発見したフーリエ は、平衡状態 における熱方程式に注目し、適当な境界条件の下で二変数のラプラス方程式
(
∂
2
∂
x
2
+
∂
2
∂
y
2
)
ϕ
(
x
,
y
)
=
0
{\displaystyle \left({\partial ^{2} \over \partial x^{2}}+{\partial ^{2} \over \partial y^{2}}\right)\phi (x,y)=0}
に帰着させて解を求めようとした。この時、フーリエは、
∑
k
=
0
∞
(
−
1
)
k
2
k
+
1
cos
(
(
2
k
+
1
)
x
)
=
π
4
,
(
−
π
2
<
x
<
π
2
)
{\displaystyle \sum _{k=0}^{\infty }{(-1)^{k} \over 2k+1}\cos((2k+1)x)={\pi \over 4},\left(-{\pi \over 2}<x<{\pi \over 2}\right)}
という三角級数を見つけている。左辺の三角関数の一つ一つは波打っているにもかかわらず、x に依らない定数に収束しているのである。
x = 0 としたときの級数は円周率 を求めるグレゴリー級数 と同じである。x の定義域を広げるとこの三角級数は n を整数として
∑
k
=
0
∞
(
−
1
)
k
2
k
+
1
cos
(
(
2
k
+
1
)
x
)
=
(
−
1
)
n
π
4
,
(
−
π
2
+
n
π
<
x
<
π
2
+
n
π
)
{\displaystyle \sum _{k=0}^{\infty }{(-1)^{k} \over 2k+1}\cos((2k+1)x)=(-1)^{n}{\pi \over 4},\left(-{\pi \over 2}+n\pi <x<{\pi \over 2}+n\pi \right)}
という矩形波 になる。このような不連続な関数まで表せることに興味を抱いたフーリエは、さらに三角級数を詳しく調べ、1822年 に出版した著書『熱の解析的理論』の中で、全ての関数は三角級数で書けるということを主張した。
微分方程式 の解の形として、三角級数を仮定するという方法は、フーリエ以前にもダニエル・ベルヌーイ らによって行われていたが、三角級数という特別な形を仮定することによって得られる特殊な解と考えられていた。フーリエの主張は、三角級数は、そのような特別なものではなく、全ての関数が三角級数で表せると大きく出ている。
フーリエの議論は飛躍が多かったため、反論が相次ぎ、この主張は受け入れられなかった。しかし、フーリエの側にだけ非があるわけではなく、当時の数学 が、このような関数列の収束性などを扱うには未熟で、フーリエの主張の真偽を判定することは難しかったことも関係している。この後、関数がフーリエ級数で表現できるための条件などを論じるために、実数 、関数 、収束 、積分 などの概念などの見直しが行われ、フーリエ級数論は19世紀数学における解析学 の厳密化に大きな影響を与えることになった。
またフーリエ級数に始まるフーリエ解析 の研究は、フーリエ変換 などの手法を産み、画像処理 やデータ圧縮 、CT 、MRI など現代科学の基礎技術としても発展していった。
f に収束するフーリエ級数が得られるときにf はフーリエ展開できる というが、f に対する形式的なフーリエ級数が収束するのか、収束するとしても本当に f に収束するのかといった複雑な議論が必要で、これはフーリエ級数の収束性問題 と呼ばれる。以下ではこれを考えずに形式的に述べることにする。
実数値関数のフーリエ級数 [ 編集 ] f は、実数 x を変数 とする実数値関数で、周期 2π の周期関数 であるとする。
a
n
=
1
π
∫
−
π
π
f
(
t
)
cos
n
t
d
t
,
(
n
=
0
,
1
,
2
,
3
,
…
)
b
n
=
1
π
∫
−
π
π
f
(
t
)
sin
n
t
d
t
,
(
n
=
1
,
2
,
3
,
…
)
{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f\left(t\right)\cos nt\,dt,\left(n=0,1,2,3,\dots \right)\\b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f\left(t\right)\sin nt\,dt,\left(n=1,2,3,\dots \right)\end{aligned}}}
と置き、a n f のフーリエ余弦係数 (Fourier cosine coefficient )、b n f のフーリエ正弦係数 (Fourier sine coefficient ) という。
これらを用いて書かれた三角級数
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
x
+
b
n
sin
n
x
)
{\displaystyle {a_{0} \over 2}+\sum _{n=1}^{\infty }\left(a_{n}\cos nx+b_{n}\sin nx\right)}
をフーリエ級数 (Fourier series ) あるいはフーリエ級数展開 (Fourier series expansion )という。余弦項だけの
a
0
2
+
∑
n
=
1
∞
a
n
cos
n
x
{\displaystyle {a_{0} \over 2}+\sum _{n=1}^{\infty }a_{n}\cos nx}
を、フーリエ余弦級数 といい、正弦項だけの
∑
n
=
1
∞
b
n
sin
n
x
{\displaystyle \sum _{n=1}^{\infty }b_{n}\sin nx}
を、フーリエ正弦級数 という。
フーリエ係数を定める積分区間 −π < x < π に制限して f をみたときに f がフーリエ級数で表される偶関数 なら、そのフーリエ級数は余弦級数となり、f (x ) がフーリエ級数で表される奇関数 なら、そのフーリエ級数は正弦級数となる。 複素数値関数のフーリエ級数(複素フーリエ級数) [ 編集 ] オイラーの公式 を用いると、複素数 型のフーリエ級数を得ることができる。f も複素数値に取ることができ
c
n
=
1
2
π
∫
−
π
π
f
(
t
)
exp
(
−
i
n
t
)
d
t
,
(
n
=
0
,
±
1
,
±
2
,
…
)
{\displaystyle c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)\exp(-int)dt,\left(n=0,\pm 1,\pm 2,\dots \right)}
を、f のフーリエ係数 (Fourier coefficient ) といい、これを用いて書かれた多項式
∑
n
=
−
m
m
c
n
e
i
n
x
{\displaystyle \sum _{n=-m}^{m}c_{n}e^{inx}}
を、m 次のフーリエ多項式 (Fourier polynomial ) という。この m を +∞ にした極限
∑
n
=
−
∞
∞
c
n
e
i
n
x
=
lim
m
→
+
∞
∑
n
=
−
m
m
c
n
e
i
n
x
{\displaystyle \sum _{n=-\infty }^{\infty }c_{n}e^{inx}=\lim _{m\to +\infty }\sum _{n=-m}^{m}c_{n}e^{inx}}
をフーリエ級数 という。左辺は
∑
n
=
−
∞
∞
c
n
e
i
n
x
=
lim
k
,
m
→
+
∞
∑
n
=
−
k
m
c
n
e
i
n
x
{\displaystyle \sum _{n=-\infty }^{\infty }c_{n}e^{inx}=\lim _{k,m\to +\infty }\sum _{n=-k}^{m}c_{n}e^{inx}}
の意味ではない ことに注意しなければならない。
周期の変更 [ 編集 ] 以上に述べたフーリエ級数は、周期 2π の周期関数 f に対する定義だが、x = (π/L ) y 2L の周期関数 g (y ) = f ((π/L )y )−L ≤ y ≤ L という区間での定義に変換でき、この形で扱われることも少なくない。
a
n
=
1
L
∫
−
L
L
g
(
s
)
cos
(
n
π
s
L
)
d
s
,
(
n
=
0
,
1
,
2
,
3
,
…
)
b
n
=
1
L
∫
−
L
L
g
(
s
)
sin
(
n
π
s
L
)
d
s
,
(
n
=
1
,
2
,
3
,
…
)
g
(
y
)
=
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
(
n
π
y
L
)
+
b
n
sin
(
n
π
y
L
)
)
c
n
=
1
2
L
∫
−
L
L
g
(
s
)
exp
(
−
i
n
π
s
L
)
d
s
,
(
n
=
0
,
±
1
,
±
2
,
…
)
g
(
y
)
=
∑
n
=
−
∞
∞
c
n
exp
(
i
n
π
y
L
)
=
lim
m
→
+
∞
∑
n
=
−
m
m
c
n
exp
(
i
n
π
y
L
)
{\displaystyle {\begin{aligned}a_{n}&={1 \over L}\int _{-L}^{L}g\left(s\right)\cos \left({\frac {n\pi s}{L}}\right)ds,\left(n=0,1,2,3,\dots \right)\\b_{n}&={\frac {1}{L}}\int _{-L}^{L}g\left(s\right)\sin \left({\frac {n\pi s}{L}}\right)ds,\left(n=1,2,3,\dots \right)\\g(y)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left(a_{n}\cos \left({\frac {n\pi y}{L}}\right)+b_{n}\sin \left({\frac {n\pi y}{L}}\right)\right)\\c_{n}&={\frac {1}{2L}}\int _{-L}^{L}g\left(s\right)\exp \left(-{\frac {in\pi s}{L}}\right)ds,\left(n=0,\pm 1,\pm 2,\dots \right)\\g(y)&=\sum _{n=-\infty }^{\infty }c_{n}\exp \left({\frac {in\pi y}{L}}\right)=\lim _{m\to +\infty }\sum _{n=-m}^{m}c_{n}\exp \left({\frac {in\pi y}{L}}\right)\end{aligned}}}
パーセバルの等式 [ 編集 ] 関数 f (x )二乗可積分 ならば、以下の等式が成り立つ:
1
π
∫
−
π
π
|
f
(
t
)
|
2
d
t
=
a
0
2
2
+
∑
n
=
1
∞
(
a
n
2
+
b
n
2
)
=
2
∑
n
=
−
∞
∞
|
c
n
|
2
.
{\displaystyle {1 \over \pi }\int _{-\pi }^{\pi }|f(t)|^{2}dt={{a_{0}}^{2} \over 2}+\sum _{n=1}^{\infty }({a_{n}}^{2}+{b_{n}}^{2})=2\sum _{n=-\infty }^{\infty }|c_{n}|^{2}.}
この式はパーセヴァルの等式 と呼ばれる。
フーリエ級数の例 [ 編集 ] f (x ) = x [ 編集 ] 周期関数 でない関数を周期関数へ拡張し、そのフーリエ級数を扱うことも多い。区間 (−π, π) で定義される関数として次のような例を考える:
f
(
x
)
=
x
(
−
π
<
x
<
π
)
.
{\displaystyle f(x)=x\quad (-\pi <x<\pi ).}
この関数 f を使って以下の周期関数 h を定義できる:
h
(
x
)
=
f
(
x
)
(
−
π
<
x
<
π
)
,
h
(
x
+
2
π
)
=
h
(
x
)
(
otherwise
)
.
{\displaystyle {\begin{aligned}h(x)&=f(x)&(-\pi <x<\pi ),\\h(x+2\pi )&=h(x)&({\text{otherwise}}).\\\end{aligned}}}
この関数 h は ..., −π, π, 3π, ... で定義 されない点に注意する。仮に定義したとして、例えば点 π 上では左極限 h (π − 0)h (π + 0)h は不連続 となる。
以降、記号を粗雑に使い、特に断りのない限り、h の意味で f を用いることにする。
f が区分的に連続微分可能 である場合、不連続点でフーリエ級数の収束値は左右からの極限の平均を取るという性質がある。定義した周期関数がフーリエ級数と一致することを求めるなら、x = π
f
(
π
)
:=
f
(
π
−
0
)
+
f
(
π
+
0
)
2
.
{\displaystyle f(\pi ):={\frac {f(\pi -0)+f(\pi +0)}{2}}.}
特に今回の場合、f (π) = 0
元の関数は奇関数 なので、f に対するフーリエ級数は正弦級数となる:
f
(
x
)
=
2
∑
n
=
1
∞
(
−
1
)
n
−
1
sin
n
x
n
.
{\displaystyle f(x)=2\sum _{n=1}^{\infty }(-1)^{n-1}{\frac {\sin nx}{n}}.}
上記より f (π / 2
π
2
=
2
∑
k
=
0
∞
(
1
4
k
+
1
−
1
4
k
+
3
)
.
{\displaystyle {\frac {\pi }{2}}=2\sum _{k=0}^{\infty }\left({\frac {1}{4k+1}}-{\frac {1}{4k+3}}\right).}
これはライプニッツの公式 として知られる。
また、パーセバルの等式 より次の関係が得られる:
1
π
∫
−
π
π
|
f
(
x
)
|
2
d
x
=
2
3
π
2
=
4
∑
n
=
1
∞
1
n
2
.
{\displaystyle {\frac {1}{\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}dx={2 \over 3}\pi ^{2}=4\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}.}
最右辺の級数はゼータ関数 の特殊値 ζ(2)
f (x ) = x 2 [ 編集 ] 前節と同様に関数 f として以下を与える:
f
(
x
)
=
x
2
(
−
π
≤
x
≤
π
)
.
{\displaystyle f(x)=x^{2}\quad (-\pi \leq x\leq \pi ).}
この場合、周期関数としての f は元となる関数の定義域の境界 −π および π 上で連続となる。
元の関数は偶関数 なので、f のフーリエ級数は余弦級数のみで表される:
f
(
x
)
=
π
2
3
+
4
∑
n
=
1
∞
(
−
1
)
n
cos
n
x
n
2
.
{\displaystyle f(x)={\pi ^{2} \over 3}+4\sum _{n=1}^{\infty }(-1)^{n}{\cos nx \over n^{2}}.}
(x 2 x になるのと同じように、この右辺の級数を微分して 2 で割ると、前節の f (x ) = x f に対する導関数のフーリエ級数とフーリエ級数の微分は一致しないが、f のフーリエ級数の微分が一様収束 するなら、導関数 f ′
さらに、この級数は f (π)
π
2
6
=
∑
n
=
1
∞
1
n
2
.
{\displaystyle {\frac {\pi ^{2}}{6}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}.}
ここでも ζ(2) が現れる。
直交性 [ 編集 ] 三角級数の直交性 [ 編集 ] フーリエ級数のようなものが考えられる背景には、関数の直交性 がある。 (−π, π) 上で定義された二乗可積分関数 の空間 L 2 (−π, π) を考える。 f (x ), g (x ) ∈ L 2 (−π, π) に対して、内積
⟨
f
(
x
)
,
g
(
x
)
⟩
:=
1
π
∫
−
π
π
f
(
x
)
g
(
x
)
∗
d
x
{\displaystyle \left\langle f(x),g(x)\right\rangle :={1 \over \pi }\int _{-\pi }^{\pi }f(x)g(x)^{*}dx}
g (x )* は g (x ) の複素共役 であり、実数値のときは、g (x ) と等しいを定義すると、自然数 m , n ≥ 1 に対し
⟨
cos
m
x
,
cos
n
x
⟩
=
δ
m
n
⟨
sin
m
x
,
sin
n
x
⟩
=
δ
m
n
⟨
cos
m
x
,
sin
n
x
⟩
=
0
⟨
1
,
1
⟩
=
2
⟨
1
,
cos
m
x
⟩
=
0
⟨
1
,
sin
m
x
⟩
=
0
{\displaystyle {\begin{aligned}\langle \cos mx,\cos nx\rangle &=\delta _{mn}\\\langle \sin mx,\sin nx\rangle &=\delta _{mn}\\\langle \cos mx,\sin nx\rangle &=0\\\langle 1,1\rangle &=2\\\langle 1,\cos mx\rangle &=0\\\langle 1,\sin mx\rangle &=0\end{aligned}}}
ただし、δmn クロネッカーのデルタ で、内積の中に用いられている 1 というのは、x に依らずに 1 を値にとる定数関数 の事とする。
このような関係から
{
1
2
,
cos
x
,
sin
x
,
cos
2
x
,
sin
2
x
,
cos
3
x
,
sin
3
x
,
…
}
{\displaystyle \left\{{\frac {1}{\sqrt {2}}},\cos x,\sin x,\cos 2x,\sin 2x,\cos 3x,\sin 3x,\ldots \right\}}
は正規直交関数列 となり、これは L 2 (−π, π) の正規直交基底 になっている。
a
n
=
⟨
f
(
x
)
,
cos
n
x
⟩
b
n
=
⟨
f
(
x
)
,
sin
n
x
⟩
{\displaystyle {\begin{aligned}a_{n}&=\langle f(x),\cos nx\rangle \\b_{n}&=\langle f(x),\sin nx\rangle \end{aligned}}}
という計算によって、それぞれ、フーリエ級数の cos nx , sin nx の係数のみを抜き出すことができる。
また、任意の自然数 m について
⟨
f
(
x
)
,
cos
m
x
⟩
=
0
⟨
f
(
x
)
,
sin
m
x
⟩
=
0
{\displaystyle {\begin{aligned}\langle f(x),\cos mx\rangle &=0\\\langle f(x),\sin mx\rangle &=0\end{aligned}}}
が成り立てば、 f (x ) = 0 となるため、この直交関数列は完備関数列 でもあり、この内積によって、 L 2 (−π, π) は、ヒルベルト空間 になる。
複素型のフーリエ級数の場合も、整数 m , n に対して
⟨
e
i
m
x
,
e
i
n
x
⟩
=
2
π
δ
m
n
{\displaystyle \langle e^{imx},e^{inx}\rangle =2\pi \delta _{mn}}
という直交関係がなりたち、{e imx
ヒルベルト空間とフーリエ級数 [ 編集 ] ヒルベルト空間 X と、その正規直交系 {e k x ∈ X に対して、その内積
⟨
x
,
e
k
⟩
{\displaystyle \langle x,e_{k}\rangle }
フーリエ係数 という。この時、ベッセルの不等式
‖
x
‖
2
2
≥
∑
k
|
⟨
x
,
e
k
⟩
|
2
{\displaystyle \|x\|_{2}^{2}\geq \sum _{k}\left|\langle x,e_{k}\rangle \right|^{2}}
が成り立つ。
さらに {e k X の基底となっていれば、三角級数のときと同様に級数
∑
k
⟨
x
,
e
k
⟩
e
k
=
⟨
x
,
e
1
⟩
e
1
+
⟨
x
,
e
2
⟩
e
2
+
⋯
{\displaystyle \sum _{k}\langle x,e_{k}\rangle e_{k}=\left\langle x,e_{1}\right\rangle e_{1}+\left\langle x,e_{2}\right\rangle e_{2}+\cdots }
が考えられ、これも同じようにフーリエ級数 という。この級数が、元の x に等しいとき、フーリエ展開できるという。そしてこの時、プランシュレルの等式
‖
x
‖
2
2
=
∑
k
|
⟨
x
,
e
k
⟩
|
2
{\displaystyle \|x\|_{2}^{2}=\sum _{k}\left|\langle x,e_{k}\rangle \right|^{2}}
が成り立つ。
ヒルベルト空間 X について、
任意の x ∈ X がフーリエ展開できること
任意の x ∈ X に対し、プランシュレルの等式が成り立つこと
{e k X の正規直交基底であること の 3つは互いに同値な条件である。
主な周期関数のフーリエ級数 [ 編集 ] 主な周期関数のフーリエ級数を示す。
関数
f
(
x
)
{\displaystyle f(x)}
0
<
x
≤
T
{\displaystyle 0<x\leq T}
a
0
,
a
n
,
b
n
{\displaystyle a_{0},a_{n},b_{n}}
時間領域
f
(
x
)
{\displaystyle f(x)}
波形
周波数領域
a
0
a
n
for
n
≥
1
b
n
for
n
≥
1
{\displaystyle {\begin{aligned}&a_{0}\\&a_{n}\quad {\text{for }}n\geq 1\\&b_{n}\quad {\text{for }}n\geq 1\end{aligned}}}
備考
出典
f
(
x
)
=
A
|
sin
(
2
π
T
x
)
|
for
0
≤
x
<
T
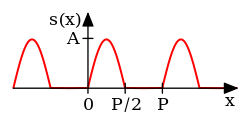
{\displaystyle f(x)=A\left|\sin \left({\frac {2\pi }{T}}x\right)\right|\quad {\text{for }}0\leq x<T}
a
0
=
4
A
π
a
n
=
{
−
4
A
π
1
n
2
−
1
n
even
0
n
odd
b
n
=
0
{\displaystyle {\begin{aligned}a_{0}=&{\frac {4A}{\pi }}\\a_{n}=&{\begin{cases}{\frac {-4A}{\pi }}{\frac {1}{n^{2}-1}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\b_{n}=&0\\\end{aligned}}}
正弦波の全波整流波形
[2] :p. 193
f
(
x
)
=
{
A
sin
(
2
π
T
x
)
for
0
≤
x
<
T
/
2
0
for
T
/
2
≤
x
<
T
{\displaystyle f(x)={\begin{cases}A\sin \left({\frac {2\pi }{T}}x\right)&\quad {\text{for }}0\leq x<T/2\\0&\quad {\text{for }}T/2\leq x<T\\\end{cases}}}
a
0
=
2
A
π
a
n
=
{
−
2
A
π
1
1
−
n
2
n
even
0
n
odd
b
n
=
{
A
2
n
=
1
0
n
>
1
{\displaystyle {\begin{aligned}a_{0}=&{\frac {2A}{\pi }}\\a_{n}=&{\begin{cases}{\frac {-2A}{\pi }}{\frac {1}{1-n^{2}}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\b_{n}=&{\begin{cases}{\frac {A}{2}}&\quad n=1\\0&\quad n>1\end{cases}}\\\end{aligned}}}
正弦波の半波整流波形
[2] :p. 193
f
(
x
)
=
{
A
for
0
≤
x
<
D
⋅
T
0
for
D
⋅
T
≤
x
<
T
{\displaystyle f(x)={\begin{cases}A&\quad {\text{for }}0\leq x<D\cdot T\\0&\quad {\text{for }}D\cdot T\leq x<T\\\end{cases}}}
a
0
=
2
A
D
a
n
=
A
n
π
sin
(
2
π
n
D
)
b
n
=
2
A
n
π
(
sin
(
π
n
D
)
)
2
{\displaystyle {\begin{aligned}a_{0}=&2AD\\a_{n}=&{\frac {A}{n\pi }}\sin \left(2\pi nD\right)\\b_{n}=&{\frac {2A}{n\pi }}\left(\sin \left(\pi nD\right)\right)^{2}\\\end{aligned}}}
0
≤
D
≤
1
{\displaystyle 0\leq D\leq 1}
D
{\displaystyle D}
f
(
x
)
=
A
x
T
for
0
≤
x
<
T
{\displaystyle f(x)={\frac {Ax}{T}}\quad {\text{for }}0\leq x<T}
a
0
=
A
a
n
=
0
b
n
=
−
A
n
π
{\displaystyle {\begin{aligned}a_{0}=&A\\a_{n}=&0\\b_{n}=&{\frac {-A}{n\pi }}\\\end{aligned}}}
ノコギリ波(増)
[2] :p. 192
f
(
x
)
=
A
−
A
x
T
for
0
≤
x
<
T
{\displaystyle f(x)=A-{\frac {Ax}{T}}\quad {\text{for }}0\leq x<T}
a
0
=
A
a
n
=
0
b
n
=
A
n
π
{\displaystyle {\begin{aligned}a_{0}=&A\\a_{n}=&0\\b_{n}=&{\frac {A}{n\pi }}\\\end{aligned}}}
ノコギリ波(減)
[2] :p. 192
f
(
x
)
=
4
A
T
2
(
x
−
T
2
)
2
for
0
≤
x
<
T
{\displaystyle f(x)={\frac {4A}{T^{2}}}\left(x-{\frac {T}{2}}\right)^{2}\quad {\text{for }}0\leq x<T}
a
0
=
2
A
3
a
n
=
4
A
π
2
n
2
b
n
=
0
{\displaystyle {\begin{aligned}a_{0}=&{\frac {2A}{3}}\\a_{n}=&{\frac {4A}{\pi ^{2}n^{2}}}\\b_{n}=&0\\\end{aligned}}}
[2] :p. 193
^ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics . Elsevier. ISBN 0125157517 ^ a b c d e Papula, Lothar (2009). Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [Mathematical Functions for Engineers and Physicists] . Vieweg+Teubner Verlag. ISBN 978-3834807571
参考文献 [ 編集 ] 関連項目 [ 編集 ]