フーリエ変換

上は時間領域で表現された矩形関数f(t)（左）と、周波数領域で表現されたそのフーリエ変換f̂(ω)（右）。f̂(ω)はSinc関数である。下は時間遅れのある矩形関数 g(t) と、そのフーリエ変換 ĝ(ω)。 時間領域における平行移動 (ディレイ)は、周波数領域では虚数部の位相シフトとして表現される。

数学においてフーリエ変換（フーリエへんかん、英: Fourier transform、FT）は、実変数の複素または実数値関数$f$を、その周波数成分を表す別の関数ˆfに写す変換である。

工学においては、変換後の関数ˆfはもとの関数$f$に含まれる周波数を記述していると考え、しばしばもとの関数$f$の周波数領域表現 (frequency domain representation) と呼ばれる。言い換えれば、フーリエ変換は関数$f$を（離散的な正弦波・余弦波の和であるフーリエ級数とは対照的に）連続的な周波数成分の集まりとして分解する操作である。

フーリエ変換 (FT) は他の多くの数学的な演算と同様にフーリエ解析の主題を成す。「フーリエ変換」という言葉は関数の周波数領域表現のことを指すこともあるし、関数を周波数領域表現へ写す変換の過程・公式を言うこともある。なおこの呼称は、19世紀フランスの数学者・物理学者で次元解析の創始者とされるジョゼフ・フーリエに由来する。

概要

フーリエ変換は、関数をその周波数成分に分解し、どの周波数がどれだけ含まれているかを示す「周波数スペクトル」に変換する数学的な操作である。この変換は、19世紀初頭にフランスの数学者・物理学者であるジョゼフ・フーリエが、熱伝導方程式の研究において、熱の伝わり方をフーリエ級数を用いて表そうとしたことに端を発する。

時間や空間に関する関数（波形など）を、その関数を構成する正弦波（または複素指数関数）の集まりとして表現し直す操作と見なすことができる。元の関数が時間領域（または空間領域）の関数 $f(t)$ であれば、フーリエ変換後の関数 ${\hat {f}}(\xi )$ は周波数領域（または波数領域）の関数となり、元の関数 $f(t)$ に周波数 $\xi$ の成分がどれだけ含まれているかを表す。

この変換は可逆であり、フーリエ逆変換と呼ばれる操作によって、周波数スペクトル ${\hat {f}}(\xi )$ から元の関数 $f(t)$ を復元することができる。

フーリエ変換は、数学におけるフーリエ解析の中心的な道具であるだけでなく、物理学、工学（特に信号処理、画像処理、通信工学）、量子力学など、現代科学の非常に広範な分野で不可欠なツールとなっている。

定義

フーリエ変換の定義には、用いる周波数の変数（周波数 $\xi$ [ヘルツ] か、角周波数 $\omega =2\pi \xi$ [ラジアン/秒] か）や、変換・逆変換の係数（正規化係数）の選び方によって、いくつかの流儀が存在する。分野によって慣習的に用いられる定義が異なるため注意が必要である。

主な定義として以下の3つが挙げられる。

よく用いられる定義のまとめ

周波数 ξ（ヘルツ）	ユニタリ	${\hat {f}}_{1}(\xi )\ {\stackrel {\mathrm {def} }{=}}\ \int _{\mathbb {R} ^{n}}f(x)e^{-2\pi ix\cdot \xi }\,dx={\hat {f}}_{2}(2\pi \xi )=(2\pi )^{n/2}{\hat {f}}_{3}(2\pi \xi )$ $f(x)=\int _{\mathbb {R} ^{n}}{\hat {f}}_{1}(\xi )e^{2\pi ix\cdot \xi }\,d\xi \$
角周波数 ω（ラジアン毎秒）	非ユニタリ	${\hat {f}}_{2}(\omega )\ {\stackrel {\mathrm {def} }{=}}\int _{\mathbb {R} ^{n}}f(x)e^{-i\omega \cdot x}\,dx\ ={\hat {f}}_{1}\left({\frac {\omega }{2\pi }}\right)=(2\pi )^{n/2}\ {\hat {f}}_{3}(\omega )$ $f(x)={\frac {1}{(2\pi )^{n}}}\int _{\mathbb {R} ^{n}}{\hat {f}}_{2}(\omega )e^{i\omega \cdot x}\,d\omega \$
	ユニタリ	${\hat {f}}_{3}(\omega )\ {\stackrel {\mathrm {def} }{=}}\ {\frac {1}{(2\pi )^{n/2}}}\int _{\mathbb {R} ^{n}}f(x)\ e^{-i\omega \cdot x}\,dx={\frac {1}{(2\pi )^{n/2}}}{\hat {f}}_{1}\left({\frac {\omega }{2\pi }}\right)={\frac {1}{(2\pi )^{n/2}}}{\hat {f}}_{2}(\omega )$ $f(x)={\frac {1}{(2\pi )^{n/2}}}\int _{\mathbb {R} ^{n}}{\hat {f}}_{3}(\omega )e^{i\omega \cdot x}\,d\omega \$

本項では、特に断りのない限り、数学や一部の信号処理の文献で用いられることのある、周波数 $\xi$（ヘルツ）を用い、変換・逆変換の係数が $1$ である定義1（ユニタリ・周波数）を採用する。この定義は、フーリエ変換と逆変換が対称形（$e$ の肩の符号が異なるだけ）である点に特徴がある。 また、この定義（および定義3）が「ユニタリ（英: unitary）」と呼ばれるのは、プランシュレルの定理で示されるように、関数の$L^{2}$ノルム（信号のエネルギーに相当）が変換前後で保存される、すなわち $\int |f(x)|^{2}dx=\int |{\hat {f}}(\xi )|^{2}d\xi$ が成り立つためであり、フーリエ変換が（$L^{2}$空間における）ユニタリ作用素であることを意味する。定義2（非ユニタリ）では、このような単純なエネルギー保存則は成立しない（係数 $1/(2\pi )^{n}$ が必要となる）。

絶対可積分関数に対する定義

絶対可積分関数 f: R → C のフーリエ変換は、

${\hat {f}}(\xi ):=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\xi },dx$

で定義される。ここでギリシャ文字小文字の ξ は任意の実数（周波数）である。

対象の関数における独立変数が物理量の場合、フーリエ変換は独立変数の次元をもとの逆数に移す。例えば、変換前の関数における独立変数 x が時間の次元をもつとき、変換後の独立変数 ξ は周波数の次元を持つ。あるいは、変換前の独立変数 x が長さの次元をもつとき、変換後の独立変数 ξ は波数の次元を持つ。この性質は定義より x ξ が無次元量であることから従う。

適当な条件のもと、f はその変換 ˆf からフーリエ逆変換 (inverse transform)

$f(x):=\int _{-\infty }^{\infty }{\hat {f}}(\xi )e^{2\pi ix\xi }\,d\xi$

によって復元することができる（x は任意の実数）。

緩増加超関数への拡張

絶対可積分でない関数、例えば $f(x)=c$ （定数関数）や $f(x)=\cos(x)$ （周期関数）、あるいはディラックのデルタ関数 $\delta (x)$ のような「関数」ではない対象についてもフーリエ変換を定義したいという強い要請が物理学や工学には存在する。

このため、フーリエ変換の定義を緩増加超関数（またはシュワルツ超関数）の空間 ${\mathcal {S}}'(\mathbb {R} )$ に拡張することが行われる。

緩増加超関数 $T$ は、シュワルツ空間 ${\mathcal {S}}(\mathbb {R} )$（急減少関数、すなわち無限回微分可能で、自身およびその全ての導関数が $|x|\to \infty$ で多項式の逆数よりも速く 0 に近づく滑らかな関数 $\phi (x)$ の集まり）上の連続線型汎関数として定義される。つまり、$T$ は各 $\phi \in {\mathcal {S}}(\mathbb {R} )$ に対して複素数 $\langle T,\phi \rangle$ を対応させる写像である。

（絶対可積分関数 $f$ も、$\langle T_{f},\phi \rangle =\int _{-\infty }^{\infty }f(x)\phi (x)dx$ により、$T_{f}$ という超関数とみなすことができる。）

シュワルツ空間 ${\mathcal {S}}(\mathbb {R} )$ はフーリエ変換 ${\mathcal {F}}$ の下で閉じている（急減少関数のフーリエ変換は再び急減少関数となる）という重要な性質を持つ。

この性質を利用し、緩増加超関数 $T$ のフーリエ変換 ${\hat {T}}={\mathcal {F}}(T)$ は、任意の急減少関数 $\phi \in {\mathcal {S}}(\mathbb {R} )$ に対して、以下の関係（プランシュレルの定理の一般化）を満たす超関数 ${\hat {T}}$ として定義される。

$\langle {\hat {T}},\phi \rangle :=\langle T,{\hat {\phi }}\rangle$

ここで ${\hat {\phi }}$ は急減少関数 $\phi$ の（絶対可積分関数としての）フーリエ変換である。この定義により、超関数のフーリエ変換は再び緩増加超関数となる。

例：定数関数 $f(x)=c$ を超関数 $T_{c}$ （$\langle T_{c},\phi \rangle =\int c\phi (x)dx$）とみなす。そのフーリエ変換 ${\hat {T}}_{c}$ は、定義より $\langle {\hat {T}}_{c},\phi \rangle =\langle T_{c},{\hat {\phi }}\rangle =c\int _{-\infty }^{\infty }{\hat {\phi }}(\xi )d\xi$ となる。 ここで、$\phi$ のフーリエ逆変換の定義 $\phi (x)=\int _{-\infty }^{\infty }{\hat {\phi }}(\xi )e^{2\pi ix\xi }d\xi$ において $x=0$ とおくと、$\phi (0)=\int _{-\infty }^{\infty }{\hat {\phi }}(\xi )d\xi$ という関係が得られる（この関係は、急減少関数 $\phi$ に対して成立する）。 したがって、$\langle {\hat {T}}c,\phi \rangle =c\phi (0)$ である。 一方、$c\delta (\xi )$ という超関数 $T{c\delta }$ は、定義により $\langle T_{c\delta },\phi \rangle =\int _{-\infty }^{\infty }c\delta (\xi )\phi (\xi )d\xi =c\phi (0)$ である。 したがって、${\hat {T}}c=T{c\delta }$、すなわち定数関数 $c$ のフーリエ変換は $c\delta (\xi )$ となる。

例：デルタ関数 $T=\delta$ （$\langle \delta ,\phi \rangle =\phi (0)$）のフーリエ変換 ${\hat {\delta }}$ は、 $\langle {\hat {\delta }},\phi \rangle =\langle \delta ,{\hat {\phi }}\rangle ={\hat {\phi }}(0)=\int _{-\infty }^{\infty }\phi (x)e^{-2\pi ix\cdot 0}dx=\int _{-\infty }^{\infty }\phi (x)dx$ これは、$f(x)=1$ という定数関数が定める超関数 $T_{1}$ の作用 $\langle T_{1},\phi \rangle =\int _{-\infty }^{\infty }1\cdot \phi (x)dx$ に等しい。 したがって、デルタ関数 $\delta (x)$ のフーリエ変換は定数関数 $1$ となる。

導入

→「フーリエ級数」も参照

この節では、フーリエ変換の「動機」の一つとして、フーリエ級数からの類推的な導入を解説する。この方法は、フーリエ変換がどのようにして関数を周波数成分の「連続的な集まり」として表現し直すかという直観的なイメージを掴む上で、歴史的にも教育的にも重要である。

フーリエ変換を考える動機はフーリエ級数の研究に始まる。フーリエ級数の研究において、複雑な周期関数は単純な波動の数学的な表現である正弦関数や余弦関数の和として表される。正弦や余弦の性質のおかげで、この和に現れる各波の量、フーリエ係数を積分によって計算することができる。

多くの場合に、${\textstyle e^{2\pi i\theta }=\cos {2\pi \theta }+i\sin {2\pi \theta }}$（オイラーの公式）を用いて、正弦関数および余弦関数の代りに基本波動 ${\textstyle e^{2\pi i\theta }}$ を用いた方が便利である。この場合には多くの公式が簡単化され、本項で後述するフーリエ変換のほかの類似の定式化をあたえるという点に優位性がある。この正弦・余弦から複素指数関数への移行にはフーリエ係数が複素数値であることを要する。この複素数は、関数に含まれる波動の振幅（あるいは大きさ）と、位相（あるいは初期角）の両方を与えているものと通常は解釈される。また、この移行に際して「負の周波数」も導入される。例えば、波動 ${\textstyle e^{2\pi i\theta }}$ および ${\textstyle e^{-2\pi i\theta }}$ はともに周期1を持つが、複素フーリエ級数においては別々の成分として取り扱われる。したがって、周波数を単純に周期の逆数と考えることはできなくなる。

フーリエ級数を以下のようにしてフーリエ変換の動機付けに用いることができる。関数 ƒ をある区間 [−L/2, L/2] の外側で 0 となるようなものとすると、任意の T ≥ L に対して ƒ を区間 [−T /2, T /2] 上のフーリエ級数に拡張できる。ここで f のフーリエ級数に現れる波動 ${\textstyle e^{2\pi inx/T}}$ の係数となる ${\textstyle c_{n}}$ で表される「量」は

${\hat {f}}{\Big (}{\dfrac {n}{T}}{\Big )}=c_{n}:=\int _{-T/2}^{T/2}e^{-2\pi inx/T}f(x)\,dx$

で与えられ、ƒ は公式

$f(x)={\frac {1}{T}}\sum _{n=-\infty }^{\infty }{\hat {f}}{\Big (}{\dfrac {n}{T}}{\Big )}e^{2\pi inx/T}$

で与えられなければならない。ξ_n = n/T とおき、Δξ = (n + 1)/T − n/T = 1/T とおくと、最後の和をリーマン和

$f(x)=\sum _{n=-\infty }^{\infty }{\hat {f}}{\Big (}{\dfrac {n}{T}}{\Big )}e^{2\pi ix\xi _{n}}\Delta \xi$

として考えることができる。T → ∞ とすることにより、このリーマン和は定義節で与えられるフーリエ逆変換（積分）に収束すると期待される。このように、フーリエ変換は、関数に含まれる個々の周波数がどの程度あるかを（スペクトル密度 ${\hat {f}}(\xi )$ として）測るものと考えることができ、それらの波動を積分（「連続和」）によって再結合して元の関数を復元する操作がフーリエ逆変換に対応する。

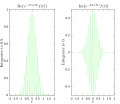
以下の画像はフーリエ変換が特定の関数に含まれる周波数を測る方法を視覚的に現したものである。関数として、（t が秒で測られる場合には）3 ヘルツで振動し、急速に 0 になる

$f(t):=\cos(6\pi t)e^{-\pi t^{2}}$

を描く。この関数は特に描画しやすい実フーリエ変換をもつものとして選ばれたものであり、最初の画像はそのグラフである。ˆf(3) を計算するために、e^−2πi(3t)ƒ(t) を積分する。二枚目の画像はこの被積分関数の実部および虚部である。被積分関数の実部は殆ど常に正となる。これは ƒ(t) が負であるときには e^−2πi(3t) の実部が同様に負となることによる。それらは同じ比率で振動するから、ƒ(t) が正であるときも同様に e^−2πi(3t) の実部も正になる。

この結果、被積分関数の実部のを積分すれば、比較的大きな数値（ここでの場合 0.5）を得ることになる。

一方、（ˆf(5) を見る場合のように）含まれない周波数を測れば、被積分関数は十分に振動し、それゆえにその積分はとても小さい値となる。一般の設定ではこれよりは少し複雑になるが、それでもフーリエ変換は関数 ƒ(t) に含まれる個々の周波数がどれくらいあるかを測るものという考え方に変わりはない。

この例では、$\cos(6\pi t)$ではなく、$\cos(6\pi t)e^{-\pi t^{2}}$と、不自然な$e^{-\pi t^{2}}$がかかっているが、$\cos(6\pi t)$は、(−∞, ∞)で絶対可積分関数としてのフーリエ変換（積分）が定義できないためである。（前述の通り、超関数としては定義可能である。）一方、$e^{-\pi t^{2}}$は、$\int _{-\infty }^{\infty }e^{-\pi t^{2}}dt=1$のため(−∞, ∞)で絶対可積分であり、$|\cos(6\pi t)e^{-\pi t^{2}}|\leq e^{-\pi t^{2}}$ が成り立つ。よって、$\cos(6\pi t)e^{-\pi t^{2}}$ は全体として絶対可積分関数となり、フーリエ変換（積分）が可能となっているものである。

• 
  3ヘルツの振動を示すもとの関数
• 
  3ヘルツにおけるフーリエ変換の被積分関数の実部および虚部
• 
  5ヘルツにおけるフーリエ変換の被積分関数の実部および虚部
• 
  3ヘルツおよび5ヘルツでラベル付けされたフーリエ変換

フーリエ変換の性質

実数直線上で定義される関数 f が絶対可積分であるとは、

$\int _{-\infty }^{\infty }|f(x)|\,dx<\infty$

を満たすルベーグ可測関数であることをいう。

基本性質

絶対可積分関数 f(x), g(x), h(x) が与えられたとき、これらのフーリエ変換をそれぞれ ˆf(ξ), ˆg(ξ), ˆh(ξ)で表す。フーリエ変換は以下の基本性質を満たす。

線型性

任意の複素数 a, b について h(x) = aƒ(x) + bg(x) であるならば

${\hat {h}}(\xi )=a\cdot {\hat {f}}(\xi )+b\cdot {\hat {g}}(\xi )$

が成り立つ。

平行移動

任意の実数 x₀ に対して h(x) = ƒ(x − x₀) であるならば

${\hat {h}}(\xi )=e^{-2\pi ix_{0}\xi }{\hat {f}}(\xi )$

が成り立つ。

変調

任意の実数 ξ₀ に対して h(x) = e^2πixξ₀ƒ(x) ならば

${\hat {h}}(\xi )={\hat {f}}(\xi -\xi _{0})$

が成り立つ。

定数倍

非零実数 a に対し、h(x) = ƒ(ax) ならば

${\hat {h}}(\xi )={\frac {1}{|a|}}{\hat {f}}{\Big (}{\frac {\xi }{a}}{\Big )}$

が成り立つ。a = −1 つまり h(x) = ƒ(−x) の場合には、時間反転性 (time-reversal property)

${\hat {h}}(\xi )={\hat {f}}(-\xi )$

が導かれる。

複素共役

f(x) の複素共役 f(x) について

${\hat {\overline {f}}}(\xi )={\overline {{\hat {f}}(-\xi )}}$

が成り立つ。

微分

関数 $f(x)$ が（$|x|\to \infty$ で 0 に収束するなどの条件を満たし）$n$ 回微分可能で、その導関数も絶対可積分であるならば、 ${\mathcal {F}}f^{(n)}(x)=(2\pi i\xi )^{n}{\hat {f}}(\xi )$ が成り立つ。逆に、 ${\mathcal {F}}={\hat {f}}^{(n)}(\xi )$ も成り立つ。この性質は、微分方程式を代数方程式に変換する上で重要である。

畳み込み

h(x) = (f ∗ g)(x) ならば

${\hat {h}}(\xi )={\hat {f}}(\xi )\cdot {\hat {g}}(\xi )$

が成り立つ。

一様連続性とリーマン・ルベーグの補題

絶対可積分関数のフーリエ変換は、常に成り立つというわけではない性質も持っている。絶対可積分関数 ƒ のフーリエ変換は一様連続で

$\|{\hat {f}}\|_{\infty }\leq \|f\|_{1}$

を満たす。絶対可積分関数のフーリエ変換は

${\hat {f}}(\xi )\to 0{\text{ as }}|\xi |\to \infty$

であることを述べたリーマン・ルベーグの補題をも満足する。絶対可積分函数 f のフーリエ変換 ˆf は有界連続だが絶対可積分であるとは限らず、その逆変換をルベーグ積分として書くことは一般にはできない。しかしながら、ƒ および ˆf がともに絶対可積分ならば、反転公式

$f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )e^{2i\pi x\xi }\,d\xi$

が殆ど全ての x において成り立つ。つまり、ƒ は右辺で定義される連続関数と殆ど至る所等しい。特に ƒ が実数直線上の連続関数として与えられたならば全ての x において等式が成り立つ。

前述の結果としてわかることは、フーリエ変換が L¹(R) 上単射であることである。

プランシュレルの定理とパーセバルの定理

f(x) および g(x) は絶対可積分であるとし、そのフーリエ変換をそれぞれ ˆf(ξ) および ˆg(ξ) と表す。f(x) および g(x) がともに自乗絶対可積分であるならばパーセバルの定理

$\int _{-\infty }^{\infty }f(x){\overline {g(x)}}\,dx=\int _{-\infty }^{\infty }{\hat {f}}(\xi ){\overline {{\hat {g}}(\xi )}}\,d\xi$

が成立する。ここで上付きバーは複素共役を表す。

パーセバルの定理と同値なプランシュレルの定理によれば

$\int _{-\infty }^{\infty }|f(x)|^{2}\,dx=\int _{-\infty }^{\infty }|{\hat {f}}(\xi )|^{2}\,d\xi$

が成立する。プランシュレルの定理により、L²(R) に属する関数の後述する意味でのフーリエ変換を定義することが可能になる。プランシュレルの定理は、フーリエ変換はもとの量のエネルギーを保存するという自然科学における解釈を持つ。著者によってはこれらの定理のどちらともをプランシュレルの定理あるいはパーセバルの定理と呼んでいる場合があるので注意を要する。

局所コンパクトアーベル群に関する文脈におけるフーリエ変換の概念の一般の定式化についてはポントリャーギン双対の項を参照されたい。

不確定性関係

→詳細は「不確定性原理」および「Hirschmanの不確定性原理」を参照

一般的に言って、f(x) が凝縮されればされるほどそのフーリエ変換 ˆf はより拡散される。特に、フーリエ変換のスケール性からわかることとして、関数を x において「圧搾」するならば、そのフーリエ変換は ξ において「伸展」される。したがって、関数とそのフーリエ変換の両方ともを勝手に凝縮させることはできない。

関数とそのフーリエ変換のコンパクト化のあいだの得失評価は不確定性関係の形で定式化することができる。ƒ(x) は絶対可積分かつ自乗絶対可積分であると仮定する。一般性を失うことなく関数 ƒ(x) は

$\int _{-\infty }^{\infty }|f(x)|^{2}\,dx=1$

に正規化されているものと仮定してよい。このとき、プランシュレルの定理により ˆf(ξ) も同様に正規化される。

x = 0 の周りでの拡散を

$D_{0}(f):=\int _{-\infty }^{\infty }x^{2}|f(x)|^{2}\,dx$

で定義される「0 の周りでの分散」(dispersion about zero) によって測ることにする。確率の言葉で言えば、これは |f(x)|² の 0 の周りでの二次のモーメントである。

このとき不確定性原理は、関数 ƒ(x) が絶対連続で、関数 x·ƒ(x) および ƒ′(x) が自乗絶対可積分であるならば

$D_{0}(f)D_{0}({\hat {f}})\geq {\frac {1}{16\pi ^{2}}}$

が成り立つことを述べる。等式が成立するのは

$f(x)=C_{1}\,e^{{-\pi x^{2}}/{\sigma ^{2}}}$

したがって、

${\hat {f}}(\xi )=\sigma C_{1}\,e^{-\pi \sigma ^{2}\xi ^{2}}$

である場合に限る。ただし、定数 σ > 0 は任意であり、係数 C₁ は ƒ を L²-正規化する定数である。言い換えれば、 ƒ は 0 を中心に持つ（正規化）ガウス関数のとき等号が成り立つ。

事実として、この不等式は任意の x₀, ξ₀ ∈ R について

${\Big [}\int _{-\infty }^{\infty }(x-x_{0})^{2}|f(x)|^{2}\,dx{\Big ]}{\Big [}\int _{-\infty }^{\infty }(\xi -\xi _{0})^{2}|{\hat {f}}(\xi )|^{2}\,d\xi {\Big ]}\geq {\frac {1}{16\pi ^{2}}}$

が成立することをも含む。

量子力学において、運動量と位置の波動関数は（プランク定数を因子に持つ）フーリエ変換対である。プランク定数でスケールしなおせば、上述の不等式はロバートソンの不確定性関係を記述する。これは、ハイゼンベルグが構想した不確定性原理そのものではないが、深い関係がある。

ポアソン和公式

→詳細は「ポアソン和公式」を参照

ポアソン和公式はフーリエ変換とフーリエ級数の間の関連性を提供する。絶対可積分関数 ƒ ∈ L¹(Rⁿ) が与えられたとき、ƒ の周期化が

${\bar {f}}(x)=\sum _{k\in \mathbb {Z} ^{n}}f(x+k)$

によって与えられる。このとき、ポアソン和公式は f のフーリエ級数を ƒ のフーリエ変換に結びつけるもので、特に f のフーリエ級数は

${\bar {f}}(x)\sim \sum _{k\in \mathbb {Z} ^{n}}{\hat {f}}(k)e^{2\pi ik\cdot x}$

で与えられることを述べるものである。ポアソン和公式を用いて、大きな次元のユークリッド球面における格子点の数に対するランダウの漸近公式を導出することができる。また、絶対可積分函数 f と ˆf がともにコンパクト台を持つならば ƒ = 0 を示すこともできる。

畳み込み定理

→詳細は「畳み込み定理」を参照

フーリエ変換は、関数の畳み込みと関数の（点毎の）積とを相互に変換する。ƒ(x) および g(x) が絶対可積分関数であるとし、そのフーリエ変換をそれぞれ ˆf(ξ) および ˆg(ξ) で表す。さらに ƒ と g との畳み込みが存在して絶対絶対可積分であるならば、この畳み込みのフーリエ変換はフーリエ変換 ˆf(ξ) と ˆg(ξ) との積で与えられる（ただし、フーリエ変換の定義の仕方によっては定数因子が現れる場合もある）。

これを式で表せば、∗ を畳み込みとして

$h(x):=(f*g)(x):=\int _{-\infty }^{\infty }f(y)g(x-y)\,dy$

と表されるとき、

${\hat {h}}(\xi )={\hat {f}}(\xi )\cdot {\hat {g}}(\xi )$

が成立することを意味する。線型時不変 (LTI) 系理論において、f(x) を単位インパルスで置き換えたものが h(x) = g(x) を与えることから、通例 g(x) は、入力 ƒ(x) と出力 h(x) に関する LTI 系のインパルス応答として解釈される。この場合、ˆg(ξ) はこの系の周波数応答を表す。

逆に、ƒ(x) がふたつの自乗絶対可積分函数 p(x) および q(x) の積に分解されるならば、 ƒ(x) のフーリエ変換は、各因子のフーリエ変換 ˆp(ξ) および ˆq(ξ) の畳み込みで与えられる。

相互相関定理

→詳細は「相互相関」を参照

同様の方法で、h(x) が ƒ(x) と g(x) との相互相関

$h(x):=(f\star g)(x):=\int _{-\infty }^{\infty }{\overline {f(y)}}\,g(x+y)\,dy$

であるならば h(x) のフーリエ変換が

${\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}\,{\hat {g}}(\xi )$

で与えられることが示される。

固有関数

L²(R) の正規直交基底の重要な一つはエルミート函数系

${\psi }_{n}(x):={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}\,e^{-\pi x^{2}}H_{n}(2x{\sqrt {\pi }})$

で与えられる。ここで H_n(x) は「確率論者の」エルミート多項式と呼ばれる、$H_{n}(x):=(-1)^{n}e^{x^{2}/2}D^{n}e^{-x^{2}/2}$ で定義される関数である。この規約の下、フーリエ変換は

${\hat {\psi }}_{n}(\xi )=(-i)^{n}{\psi }_{n}(\xi )$

で与えられる。言い換えれば、エルミート関数系は L²(R) 上のフーリエ変換の固有関数からなる完全正規直交系を成す。しかしながら、この固有関数系の選び方は一意ではなく、フーリエ変換の相異なる固有値は {±1, ±i} の 4 つしかなく、同じ固有値に属する固有関数の任意の線型結合はふたたび固有関数になる。この結果として L²(R) を 4 つの空間 H₀, H₁, H₂, H₃ で、フーリエ変換が H_k 上で単に i^k-倍として作用するものの直和に分解することができる。この方法によるフーリエ変換の定義はウィーナーによる。エルミート関数を選ぶのが便利なのは、それらが周波数域と時間域の両方で指数関数的に局在することと、それゆえに時間周波数解析において用いられる非整数次フーリエ変換が得られることにある 。

球面調和関数

→詳細は「球面調和関数系」を参照

${\mathcal {A}}_{k}$ で次数 k の斉次調和多項式全体の成す集合を表す。集合 ${\mathcal {A}}_{k}$ は体球面調和関数系として知られる。高次元において体球面調和関数系はエルミート多項式と同様の役割を演じる。具体的には、${\mathcal {A}}_{k}$ の適当な P(x) に対し、f(x) = e^−π|x|2P(x) のフーリエ変換は

${\hat {f}}(\xi )=i^{-k}f(\xi )$

で与えられる。集合 ${\mathcal {H}}_{k}$ を f(|x|)P(x) (P(x) ∈ ${\mathcal {A}}_{k}$) の形の関数から作られる線型結合全体の成す集合の L²(Rⁿ) における閉包とする。このとき、空間 L²(Rⁿ) は空間 ${\mathcal {H}}_{k}$ の直和に分解され、フーリエ変換は各空間 ${\mathcal {H}}_{k}$ をそれ自身に移す。また、各空間 ${\mathcal {H}}_{k}$ へのフーリエ変換の作用を特徴付けることができる。ƒ(x) = ƒ₀(|x|)P(x) (P(x) ∈ ${\mathcal {A}}_{k}$) と表される関数のフーリエ変換は

${\hat {f}}(\xi )=F_{0}(|\xi |)P(\xi )$

となる。ただし、

$F_{0}(r)=2\pi i^{-k}r^{-(n+2k-2)/2}\int _{0}^{\infty }f_{0}(s)J_{(n+2k-2)/2}(2\pi rs)s^{(n+2k)/2}\,ds$

であり、J_{(n + 2k − 2)/2} は次数 (n + 2k − 2)/2 の第一種ベッセル関数である。k = 0 のとき、これは動径関数のフーリエ変換に対する有用な公式を与える。

一般化

他の函数空間上のフーリエ変換

フーリエ変換の定義を他の函数空間に対するものへ拡張することができる。コンパクト台を持つ滑らかな函数は絶対可積分で、その全体は L²(R) において稠密であるから、プランシュレルの定理を用いて、L²(R) の一般の函数にまで（コンパクト台をもつ滑らかな函数によって近似して）フーリエ変換の定義を拡張することができる。さらに

${\mathcal {F}}\colon L^{2}(\mathbb {R} )\to L^{2}(\mathbb {R} )$

はユニタリ作用素である。フーリエ変換の多くの性質はこの場合にもそのまま成立する。ハウスドルフ・ヤング不等式を用いて 1 ≤ p ≤ 2 に対する L^p(R) の函数を含むようにフーリエ変換の定義を拡張することができる。

だが、さらなる拡張はもっと技巧的である。2 < p < ∞ の範囲でのL^p に属する函数のフーリエ変換には超函数の研究が必要である。事実として、p > 2 に関する L^p に属する函数のフーリエ変換は函数としては定義できないことを示すことができる 。

多次元版

フーリエ変換は勝手な次元 n において考えることができる。1-次元の場合と同様にさまざまな流儀があるが、本項では絶対可積分函数 ƒ(x) に対して、

${\hat {f}}(\xi )={\mathcal {F}}(f)(\xi )=\int _{\mathbb {R} ^{n}}f(x)e^{-2\pi ix\cdot \xi }\,dx$

をフーリエ変換の定義とする。ここで、x および ξ は n-次元ベクトルであり、x · ξ はベクトルの点乗積である。点乗積はしばしば <x, ξ> とも書き表される。

プランシュレルの定理やパーセバルの定理がそうであるように、上述の基本性質は n-次元フーリエ変換においても成立する。函数が絶対可積分であるとき、フーリエ変換はやはり一様連続であり、リーマン・ルベーグの補題が成立する。

より高い次元ではフーリエ変換の制限問題の研究が興味深いものになる。絶対可積分函数のフーリエ変換は連続で、この函数の任意の集合への制限が定義される。しかし自乗絶対可積分函数のフーリエ変換は自乗絶対可積分函数の一般の類を成す。そのような L²(Rⁿ)-函数のフーリエ変換の制限は測度 0 の集合上では定義することができない。1 ≤ p ≤ 2 に対する L^p における制限問題の理解はいまだ活発な研究の行われる領域である。驚くべきことに、集合 S の曲率が非零であるようないくつかの場合には、フーリエ変換の S への制限を定義することができる。S が Rⁿ における単位球面であるときが特に興味深い。この場合に、トマス-ステインの制限定理によれば、フーリエ変換の Rⁿ における単位球面への制限は 1 ≤ p ≤ (2n + 2)/(n + 3) に対する L^p 上で有界作用素である。

1-次元の場合と多次元の場合とで、フーリエ変換の大きな違いは部分和作用素に関係する。与えられた絶対可積分函数 ƒ に対し

$f_{R}(x)=\int _{S_{R}}{\hat {f}}(\xi )e^{2\pi ix\cdot \xi }\,d\xi ,\quad x\in \mathbb {R} ^{n}$

で定義される函数 ƒ_R を考える。さらに ƒ が L^p(Rⁿ) に属すると仮定する。n = 1 で 1 < p < ∞ とし、S_R = (−R, R) と置くと、ヒルベルト変換の有界性から ƒ_R は R を無限大に飛ばす極限で ƒ に L^p 内で収束する。素朴に n > 1 の場合にも同様であることを期待するかもしれない。S_R を一辺の長さが R の立方体とするならば、確かに部分和作用素はもとの函数に収束する。別の自然な候補としてユークリッド球体 S_R = {ξ : |ξ| < R} をとると、部分和作用素が収束するためには単位球体に対するマルチプライヤーが L^p(Rⁿ) において有界である必要がある。n ≥ 2 に対しては、単位球体に対するマルチプライヤーは p = 2 でない限り有界にはならないというよく知られたチャールズ・フェファーマンの定理がある。事実として、p ≠ 2 のときには ƒ_R が ƒ に L^p 内で収束しないだけではなく、函数 ƒ ∈ L^p(Rⁿ) であっても ƒ_R が L^p の元でさえないようなものまでが存在する。

フーリエ・スティルチェス変換

Rⁿ 上の有限ボレル測度 μ のフーリエ変換は

${\hat {\mu }}(\xi )=\int _{\mathbb {R} ^{n}}e^{-2\pi ix\cdot \xi }\,d\mu$

によって与えられる。この変換は絶対可積分函数のフーリエ変換がもつ多くの性質を引き続き満足する。大きな違いの一つに、測度に関してリーマン・ルベーグの補題が成り立たないことが挙げられる。dμ = ƒ(x)dx の場合には上述の定義式を f の通常のフーリエ変換の定義に簡約化することができる。

このフーリエ変換を用いて連続測度の特徴づけを与えることができる。ボホナーの定理はそのような函数を測度のフーリエ・スティルチェス変換として得られるものとして特徴付ける。

さらに言えば、ディラックのデルタ函数は函数ではないが有限ボレル測度であり、そのフーリエ変換は定数函数となる（特殊値は用いるフーリエ変換の形に依存する）。

局所コンパクトアーベル群

フーリエ変換を任意の局所コンパクトアーベル群に対して一般化することができる。局所コンパクトアーベル群とは、抽象アーベル群であると同時に局所コンパクトなハウスドルフ空間であって、なおかつその位相に関して群演算が連続となるものである。G が局所コンパクトアーベル群ならば、G はハール測度と呼ばれる平行移動不変な測度 μ を持つ。また、局所コンパクトアーベル群 G に対して、その位相を指標全体の成す集合 ˆG へ移行することができて、ˆG 自身も局所コンパクトアーベル群の構造を持つ。L¹(G) に属する函数 f に対して、そのフーリエ変換を

${\hat {f}}(\xi )=\int _{G}\xi (x)f(x)\,d\mu \qquad \left(\forall \ \xi \in {\hat {G}}\right)$

によって定義することができる。

この一般化を概周期函数に適用した理論や、準周期函数に適用した理論が知られている。

応用

→詳細は「フーリエ変換の応用」を参照

フーリエ変換は、関数を周波数成分に分解するというその性質から、理論的な解析から実践的なデータ処理まで、科学・工学の極めて広い分野で応用されている。

微分方程式の解析学

フーリエ変換は、微分作用素を（周波数変数に関する）単純な掛け算に変換する性質を持つ。例えば、関数 $f(x)$ の導関数 $f'(x)$ のフーリエ変換は $2\pi i\xi {\hat {f}}(\xi )$ となる（定義による定数の違いあり）。この性質を利用することで、線型微分方程式を、周波数領域における代数方程式に変換して解くことができる。

特に、熱伝導方程式や波動方程式、シュレーディンガー方程式のような偏微分方程式の解法において強力な道具となる。フーリエがこの変換を導入した直接の動機も、熱伝導方程式の解析であった。

信号処理

信号処理は、フーリエ変換の最も代表的な応用分野の一つである。

• スペクトル解析: 音声信号や電波などの時間信号 $f(t)$ をフーリエ変換することで、その信号に含まれる周波数成分 ${\hat {f}}(\xi )$（周波数スペクトル）を知ることができる。これにより、信号の特性分析、ノイズの同定、特定の周波数成分の検出などが可能となる。

• フィルタリング: 信号から特定の周波数成分を除去（例：ノイズ除去）したり、特定の周波数成分のみを通過させたりする操作（フィルタリング）は、周波数領域で容易に行うことができる。例えば、不要な高周波成分を除去するローパスフィルタは、周波数領域で ${\hat {f}}(\xi )$ に特定の関数（高周波域で0になる関数）を掛け合わせ、それを逆フーリエ変換することで実現される。これは、畳み込み定理に基づいている。

• 非定常信号の解析: 実際の音声や音楽のように、時間と共に周波数成分が変化する信号（非定常信号）を解析するためには、短時間フーリエ変換 (STFT) やウェーブレット変換が用いられる。これらは、時間領域の局所的な区間（窓関数を適用した区間）に対してフーリエ変換を繰り返し適用する手法である。

画像処理

2次元フーリエ変換は、デジタル画像処理において広く用いられる。画像は空間的な輝度（または色）の分布であり、そのフーリエ変換は空間周波数（画像の模様の細かさや向き）のスペクトルを表す。

• 画像フィルタリング: 信号処理と同様に、周波数領域での操作により、画像のノイズ除去、エッジ強調、ぼかし処理などが行われる。

• 画像圧縮: JPEGなどの画像圧縮規格は、画像を小さなブロックに分割し、離散コサイン変換（フーリエ変換の変種）を用いて空間周波数成分に変換し、人間の視覚が敏感でない高周波成分の情報を削減することでデータ量を圧縮している。

量子力学

量子力学において、粒子の状態は波動関数 $\psi (x)$ で記述される。位置 $x$ に関する波動関数 $\psi (x)$ と、運動量 $p$ に関する波動関数 $\phi (p)$ は、互いにフーリエ変換（の定数倍）の関係にある。

$\phi (p)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\psi (x)e^{-ipx/\hbar }dx$

この関係は、粒子の位置と運動量を同時に正確に決定することはできないという不確定性原理の数学的な表現（不確定性関係）と密接に関連している。

離散フーリエ変換

→詳細は「離散フーリエ変換」および「高速フーリエ変換」を参照

現実の信号処理や画像処理では、コンピュータを用いて数値的にフーリエ変換を計算する必要がある。この目的で用いられるのが、連続的な関数ではなく、離散的な（サンプリングされた）データ列を扱う離散フーリエ変換（英: Discrete Fourier Transform, DFT）である。

DFTは、有限個のデータ点 $x_{0},x_{1},\dots ,x_{N-1}$ から、有限個の周波数成分 $X_{0},X_{1},\dots ,X_{N-1}$ を計算する変換であり、その計算を劇的に高速化するアルゴリズムが高速フーリエ変換（英: Fast Fourier Transform, FFT）である。

FFTの登場により、膨大なデータに対しても実用的な時間でフーリエ変換（およびその逆変換）が計算可能となり、上記のような信号処理や画像処理の応用が爆発的に普及する基盤となった。

フーリエ変換の定義域と値域のまとめ

フーリエ変換は、定義する関数の空間（定義域）によって、変換後の関数の属する空間（値域）が異なる。主な空間と変換の性質を以下にまとめる。

• シュワルツ空間 ${\mathcal {S}}(\mathbb {R} )$: 急減少関数の空間。フーリエ変換は ${\mathcal {S}}(\mathbb {R} )$ から ${\mathcal {S}}(\mathbb {R} )$ への全単射であり、この空間で閉じている。（詳細は超関数への拡張を参照）
• $L^{1}$空間 $L^{1}(\mathbb {R} )$: 絶対可積分関数の空間。フーリエ変換 ${\mathcal {F}}$ は $L^{1}(\mathbb {R} )$ から $C_{0}(\mathbb {R} )$（無限遠で 0 に収束する連続関数の空間）への有界線型写像である（リーマン・ルベーグの補題）。
• $L^{2}$空間 $L^{2}(\mathbb {R} )$: 自乗可積分関数の空間。フーリエ変換は $L^{2}(\mathbb {R} )$ から $L^{2}(\mathbb {R} )$ へのユニタリ作用素である（プランシュレルの定理）。ただし、この空間での変換は、必ずしも積分として定義されるとは限らず、極限操作によって定義される。（詳細は一般化を参照）
• $L^{p}$空間（$1<p<2$）: フーリエ変換は $L^{p}(\mathbb {R} )$ から $L^{q}(\mathbb {R} )$ への有界線型写像である（$1/p+1/q=1$）。（ハウスドルフ・ヤング不等式）
• 緩増加超関数 ${\mathcal {S}}'(\mathbb {R} )$: シュワルツ空間の双対空間。フーリエ変換は ${\mathcal {S}}'(\mathbb {R} )$ から ${\mathcal {S}}'(\mathbb {R} )$ への全単射であり、閉じている。これにより、デルタ関数や定数関数など、$L^{1}$ や $L^{2}$ に属さない対象のフーリエ変換も定義可能となる。（詳細は超関数への拡張を参照）

その他の記法

フーリエ変換の記法として ˆf(ξ) 以外によく用いられるものに

$F(\xi ),\quad {\mathcal {F}}(f)(\xi ),\quad ({\mathcal {F}}f)(\xi ),\quad {\mathcal {F}}(f(t))$

などがある。あるいはもっと他の記号を使うことも在りうる。たとえば、（f(x) と F(ξ) のように）もとの函数を表している文字の対応する大文字を用いてそのフーリエ変換を表すことは自然科学や工学においてとくによく用いられる記法である。

複素函数 ˆf(ξ) は、極座標に関してこれを表示することにより、振幅

$A(\xi )=|{\hat {f}}(\xi )|,$

および位相

$\varphi (\xi )=\arg({\hat {f}}(\xi ))$

と呼ばれるふたつの実函数 A(ξ) および φ(ξ) を用いて

${\hat {f}}(\xi )=A(\xi )e^{i\varphi (\xi )}$

なる形に解釈することができる。

このとき逆変換は ƒ(x) の周波数成分すべての再結合として

$f(x)=\int _{-\infty }^{\infty }A(\xi )\,e^{i(2\pi \xi x+\varphi (\xi ))}\,d\nu$

と書くことができる。各成分は振幅が A(ξ) で（x = 0 における）初期位相角が φ(ξ) であるような e^2πixξ のかたちの複素正弦曲線である。

フーリエ変換は函数空間の間の写像として考えることもできる。この写像はここでは ${\mathcal {F}}$ で表し、函数 f のフーリエ変換には ${\mathcal {F}}(f)$ が用いられる。この写像 ${\mathcal {F}}$ は函数空間上の線型変換とみることができ、それによって ${\mathcal {F}}(f)$ と書く代わりに、ベクトル（ここでは函数 f）の線型変換を表す線型代数学の標準的な記法で ${\mathcal {F}}f$ と書くこともできる。函数にフーリエ変換を施した結果は再び函数となるから、この新たな函数の ξ における値というものには意味があり、それを ${\mathcal {F}}(f)(\xi )$ あるいは $({\mathcal {F}}f)(\xi )$ などと表す。前者の場合には ${\mathcal {F}}$ はまず f に施されて、その後に得られた函数の ξ における値が評価されるものと暗黙に理解されているということに注意しなければならない。なお、混乱を防ぐため（そしてラプラス変換の記法と統一して）括弧の種類を変えて${\mathcal {F}}[f](\xi )$のように書く場合もある。

数学や多くの応用科学において、函数 f それ自身と函数 f の変数 x における値 f(x) とを峻別しなければならないことがしばしばある。このことが意味するのは、たとえば${\mathcal {F}}(f(x))$ のような記法は、形式的には f の x における「値」のフーリエ変換と解釈できてしまうということである。このような不具合にもかかわらず、特定の函数あるいは特定の変数の函数を頻繁に変換しなければならないような場合には、このような記法はよく用いられる。たとえば

${\mathcal {F}}(\mathrm {rect} (x))=\mathrm {sinc} (\xi )$

は矩形函数のフーリエ変換が sinc-函数であることを表すために用いられることがあり、またたとえば

${\mathcal {F}}(f(x+x_{0}))={\mathcal {F}}(f(x))e^{2\pi i\xi x_{0}}$

はフーリエ変換のシフト性を表すのに用いられることがある。最後の例は、変換される函数 f をx₀ のではなく x の函数であるという前提のもとでのみ正しいということに注意を要する。

主なフーリエ変換の一覧

以下にフーリエ変換の閉じた表示に関する表を掲げる（フーリエ変換はよく用いられる三種類を挙げてある）。函数 ƒ(x) , g(x), h(x) に対して、それらのフーリエ変換をそれぞれ ˆf, ˆg, ˆh で表す。

函数の関係式

以下の表におけるフーリエ変換は (Erdélyi 1954) あるいは (Kammler 2000) の付録に見つけることができる。

	もとの函数	ユニタリ・周波に関するフーリエ変換	ユニタリ・角周波に関するフーリエ変換	非ユニタリ・角周波に関するフーリエ変換	備考
	$f(x)\,$	${\hat {f}}(\xi )=$ $\int \limits _{-\infty }^{\infty }f(x)e^{-2\pi ix\xi }dx$	${\hat {f}}(\omega )=$${\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(x)e^{-i\omega x}dx$	${\hat {f}}(\nu )=$ $\int \limits _{-\infty }^{\infty }f(x)e^{-i\nu x}dx$
101	$af(x)+bg(x)\,$	$a{\hat {f}}(\xi )+b{\hat {g}}(\xi )\,$	$a{\hat {f}}(\omega )+b{\hat {g}}(\omega )\,$	$a{\hat {f}}(\nu )+b{\hat {g}}(\nu )\,$	線型性
102	$f(x-a)\,$	$e^{-2\pi ia\xi }{\hat {f}}(\xi )\,$	$e^{-ia\omega }{\hat {f}}(\omega )\,$	$e^{-ia\nu }{\hat {f}}(\nu )\,$	時間領域シフト
103	$e^{2\pi iax}f(x)\,$	${\hat {f}}\left(\xi -a\right)\,$	${\hat {f}}(\omega -2\pi a)\,$	${\hat {f}}(\nu -2\pi a)\,$	周波数領域シフト 102の双対
104	$f(ax)\,$	${\frac {1}{|a|}}{\hat {f}}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{|a|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$	${\frac {1}{|a|}}{\hat {f}}\left({\frac {\nu }{a}}\right)\,$	|a| が大きければ f(ax) は 0 の周りに集中し ${\frac {1}{|a|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$ は平らに広がる
105	${\hat {f}}(x)\,$	$f(-\xi )\,$	$f(-\omega )\,$	$2\pi f(-\nu )\,$	ここで、${\hat {f}}$ は、それぞれの列で考えているフーリエ変換を施した結果の、変数を x に取替えたものである。
106	${\frac {d^{n}f(x)}{dx^{n}}}\,$	$(2\pi i\xi )^{n}{\hat {f}}(\xi )\,$	$(i\omega )^{n}{\hat {f}}(\omega )\,$	$(i\nu )^{n}{\hat {f}}(\nu )\,$
107	$x^{n}f(x)\,$	$\left({\frac {i}{2\pi }}\right)^{n}{\frac {d^{n}{\hat {f}}(\xi )}{d\xi ^{n}}}\,$	$i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}$	$i^{n}{\frac {d^{n}{\hat {f}}(\nu )}{d\nu ^{n}}}$	106の双対
108	$(f*g)(x)\,$	${\hat {f}}(\xi ){\hat {g}}(\xi )\,$	${\sqrt {2\pi }}{\hat {f}}(\omega ){\hat {g}}(\omega )\,$	${\hat {f}}(\nu ){\hat {g}}(\nu )\,$	f ∗ g は f と g との畳み込みである。この公式は畳み込み定理と呼ばれる。
109	$f(x)g(x)\,$	$({\hat {f}}*{\hat {g}})(\xi )\,$	$({\hat {f}}*{\hat {g}})(\omega ) \over {\sqrt {2\pi }}\,$	${\frac {1}{2\pi }}({\hat {f}}*{\hat {g}})(\nu )\,$	108の双対
110	純実偶関数$f(x)$	${\hat {f}}(\omega ),\,{\hat {f}}(\xi ),\,{\hat {f}}(\nu )\,$ はいずれも純実偶関数			正弦・余弦変換も参照
111	純実奇関数$f(x)$	${\hat {f}}(\omega ),\,{\hat {f}}(\xi ),\,{\hat {f}}(\nu )$ はいずれも純虚奇関数

自乗絶対可積分函数

以下の表におけるフーリエ変換は (Campbell & Foster 1948), (Erdélyi 1954) あるいは (Kammler 2000) の付録に見つけることができる。

	もとの函数	ユニタリ・周波に関するフーリエ変換	ユニタリ・角周波に関するフーリエ変換	非ユニタリ・角周波に関するフーリエ変換	備考
	$f(x)$	${\hat {f}}(\xi )=$ $\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\xi }\,dx$	${\hat {f}}(\omega )=$ ${\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx$	${\hat {f}}(\nu )=$ $\int _{-\infty }^{\infty }f(x)e^{-i\nu x}\,dx$
201	$\operatorname {rect} (ax)\,$	${\frac {1}{|a|}}\cdot \operatorname {sinc} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {sinc} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {sinc} \left({\frac {\nu }{2\pi a}}\right)$	矩形波と標準化されたsinc関数でsinc関数はsinc(x) = sin(πx)/(πx)で表される
202	$\operatorname {sinc} (ax)\,$	${\frac {1}{|a|}}\cdot \operatorname {rect} \left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {rect} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {rect} \left({\frac {\nu }{2\pi a}}\right)$	201の双対で矩形波は理想的なローパスフィルターである。sinc関数はそのようなフィルターの非因果波応答である。
203	$\operatorname {sinc} ^{2}(ax)$	${\frac {1}{|a|}}\cdot \operatorname {tri} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {tri} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {tri} \left({\frac {\nu }{2\pi a}}\right)$	tri(x)は三角形関数である。
204	$\operatorname {tri} (ax)$	${\frac {1}{|a|}}\cdot \operatorname {sinc} ^{2}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {sinc} ^{2}\left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {sinc} ^{2}\left({\frac {\nu }{2\pi a}}\right)$	203の双対
205	$e^{-ax}u(x)\,$	${\frac {1}{a+2\pi i\xi }}$	${\frac {1}{{\sqrt {2\pi }}(a+i\omega )}}$	${\frac {1}{a+i\nu }}$	u(x)はヘビサイドの単位ステップ関数であり、a>0
206	$e^{-\alpha x^{2}}\,$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{-{\frac {(\pi \xi )^{2}}{\alpha }}}$	${\frac {1}{\sqrt {2\alpha }}}\cdot e^{-{\frac {\omega ^{2}}{4\alpha }}}$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{-{\frac {\nu ^{2}}{4\alpha }}}$	これが示すものは、ガウス関数exp(−αx2)でαを選んだ場合はユニタリフーリエ変換である。 Re(α)>0で積分可能である
207	$\operatorname {e} ^{-a|x|}\,$	${\frac {2a}{a^{2}+4\pi ^{2}\xi ^{2}}}$	${\sqrt {\frac {2}{\pi }}}\cdot {\frac {a}{a^{2}+\omega ^{2}}}$	${\frac {2a}{a^{2}+\nu ^{2}}}$	a>0である
208	${\frac {J_{n}(x)}{x}}\,$	${\frac {2i}{n}}(-i)^{n}\cdot U_{n-1}(2\pi \xi )\,$   $\cdot \ {\sqrt {1-4\pi ^{2}\xi ^{2}}}\operatorname {rect} (\pi \xi )$	${\sqrt {\frac {2}{\pi }}}{\frac {i}{n}}(-i)^{n}\cdot U_{n-1}(\omega )\,$   $\cdot \ {\sqrt {1-\omega ^{2}}}\operatorname {rect} \left({\frac {\omega }{2}}\right)$	${\frac {2i}{n}}(-i)^{n}\cdot U_{n-1}(\nu )\,$   $\cdot \ {\sqrt {1-\nu ^{2}}}\operatorname {rect} \left({\frac {\nu }{2}}\right)$	関数Jn (x)は、n次の第1種ベッセル関数である。関数Un (x)は第2種チェビシェフ多項式である。下記315と316を参照
209	$\operatorname {sech} (ax)\,$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi ^{2}}{a}}\xi \right)$	${\frac {1}{a}}{\sqrt {\frac {\pi }{2}}}\operatorname {sech} \left({\frac {\pi }{2a}}\omega \right)$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi }{2a}}\nu \right)$	双曲線正割は自分自身をフーリエ変換したものである

超函数

以下の表におけるフーリエ変換は (Erdélyi 1954) あるいは (Kammler 2000) の付録に見つけることができる。

	もとの函数	ユニタリ・周波に関するフーリエ変換	ユニタリ・角周波に関するフーリエ変換	非ユニタリ・角周波に関するフーリエ変換	備考
	$f(x)\,$	${\hat {f}}(\xi )=$ $\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\xi }\,dx$	${\hat {f}}(\omega )=$ ${\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx$	${\hat {f}}(\nu )=$ $\int _{-\infty }^{\infty }f(x)e^{-i\nu x}\,dx$
301	$1$	$\delta (\xi )\,$	${\sqrt {2\pi }}\cdot \delta (\omega )$	$2\pi \delta (\nu )\,$	δ(ξ) はディラックのデルタ関数
302	$\delta (x)\,$	$1$	${\frac {1}{\sqrt {2\pi }}}\,$	$1$	301の双対
303	$e^{iax}\,$	$\delta \left(\xi -{\frac {a}{2\pi }}\right)$	${\sqrt {2\pi }}\cdot \delta (\omega -a)$	$2\pi \delta (\nu -a)\,$	103と301より導かれる。
304	$\cos(ax)\,$	${\frac {\displaystyle \delta \left(\xi -{\frac {a}{2\pi }}\right)+\delta \left(\xi +{\frac {a}{2\pi }}\right)}{2}}$	${\sqrt {2\pi }}\cdot {\frac {\delta (\omega -a)+\delta (\omega +a)}{2}}\,$	$\pi \left(\delta (\nu -a)+\delta (\nu +a)\right)$	101、303とオイラーの公式：$\displaystyle \cos(ax)=(e^{iax}+e^{-iax})/2.$より導かれる。
305	$\sin(ax)\,$	$i\cdot {\frac {\displaystyle \delta \left(\xi +{\frac {a}{2\pi }}\right)-\delta \left(\xi -{\frac {a}{2\pi }}\right)}{2}}$	$i{\sqrt {2\pi }}\cdot {\frac {\delta (\omega +a)-\delta (\omega -a)}{2}}$	$i\pi \left(\delta (\nu +a)-\delta (\nu -a)\right)$	101、303と $\displaystyle \sin(ax)=(e^{iax}-e^{-iax})/(2i).$ より導かれる。
306	$\cos(ax^{2})\,$	${\sqrt {\frac {\pi }{a}}}\cos \left({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac {\pi }{4}}\right)$	${\frac {1}{\sqrt {2a}}}\cos \left({\frac {\omega ^{2}}{4a}}-{\frac {\pi }{4}}\right)$	${\sqrt {\frac {\pi }{a}}}\cos \left({\frac {\nu ^{2}}{4a}}-{\frac {\pi }{4}}\right)$
307	$\sin(ax^{2})\,$	$-{\sqrt {\frac {\pi }{a}}}\sin \left({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac {\pi }{4}}\right)$	${\frac {-1}{\sqrt {2a}}}\sin \left({\frac {\omega ^{2}}{4a}}-{\frac {\pi }{4}}\right)$	$-{\sqrt {\frac {\pi }{a}}}\sin \left({\frac {\nu ^{2}}{4a}}-{\frac {\pi }{4}}\right)$
308	$x^{n}\,$	$\left({\frac {i}{2\pi }}\right)^{n}\delta ^{(n)}(\xi )\,$	$i^{n}{\sqrt {2\pi }}\delta ^{(n)}(\omega )\,$	$2\pi i^{n}\delta ^{(n)}(\nu )\,$	n は自然数、 δ(n )(ξ) はディラックのデルタ関数のn 階微分。107と301より導かれる。さらに101と組み合わせることで、任意の多項式を変換できる。
309	${\frac {1}{x}}\,$	$-i\pi \operatorname {sgn}(\xi )\,$	$-i{\sqrt {\frac {\pi }{2}}}\operatorname {sgn}(\omega )$	$-i\pi \operatorname {sgn}(\nu )\,$	sgn(ξ) は符号関数。1/x は超関数ではないことに注意。シュワルツ関数に対してテストするときにコーシーの主値を使用する必要がある。この規則はヒルベルト変換を研究するとき有用である。
310	${\frac {1}{x^{n}}}$	$-i\pi {\frac {(-2\pi i\xi )^{n-1}}{(n-1)!}}\operatorname {sgn}(\xi )$	$-i{\sqrt {\frac {\pi }{2}}}\cdot {\frac {(-i\omega )^{n-1}}{(n-1)!}}\operatorname {sgn}(\omega )$	$-i\pi {\frac {(-i\nu )^{n-1}}{(n-1)!}}\operatorname {sgn}(\nu )$	309の一般化
311	${\frac {1}{\sqrt {|x|}}}\,$	${\frac {1}{\sqrt {|\xi |}}}$	${\frac {1}{\sqrt {|\omega |}}}$	${\frac {\sqrt {2\pi }}{\sqrt {|\nu |}}}$
312	$\operatorname {sgn}(x)\,$	${\frac {1}{i\pi \xi }}$	${\sqrt {\frac {2}{\pi }}}\cdot {\frac {1}{i\omega }}\,$	${\frac {2}{i\nu }}$	309の双対。積分はコーシーの主値を考える。
313	$u(x)\,$	${\frac {1}{2}}\left({\frac {1}{i\pi \xi }}+\delta (\xi )\right)$	${\sqrt {\frac {\pi }{2}}}\left({\frac {1}{i\pi \omega }}+\delta (\omega )\right)$	$\pi \left({\frac {1}{i\pi \nu }}+\delta (\nu )\right)$	u (x ) はヘヴィサイドの階段関数。101、301および312より導かれる。
314	$\sum _{n=-\infty }^{\infty }\delta (x-nT)$	${\frac {1}{T}}\sum _{k=-\infty }^{\infty }\delta \left(\xi -{\frac {k}{T}}\right)$	${\frac {\sqrt {2\pi }}{T}}\sum _{k=-\infty }^{\infty }\delta \left(\omega -{\frac {2\pi k}{T}}\right)$	${\frac {2\pi }{T}}\sum _{k=-\infty }^{\infty }\delta \left(\nu -{\frac {2\pi k}{T}}\right)$	この関数はくし型関数といわれる。302、102および、超関数として $\sum _{n=-\infty }^{\infty }e^{inx}=\sum _{k=-\infty }^{\infty }\delta (x+2\pi k)$ であることから導かれる。
315	$J_{0}(x)\,$	${\frac {2\,\operatorname {rect} (\pi \xi )}{\sqrt {1-4\pi ^{2}\xi ^{2}}}}$	${\sqrt {\frac {2}{\pi }}}\cdot {\frac {\operatorname {rect} \left(\displaystyle {\frac {\omega }{2}}\right)}{\sqrt {1-\omega ^{2}}}}$	${\frac {2\,\operatorname {rect} \left(\displaystyle {\frac {\nu }{2}}\right)}{\sqrt {1-\nu ^{2}}}}$	J0 (x ) は0次の第1種ベッセル関数
316	$J_{n}(x)\,$	${\frac {2(-i)^{n}T_{n}(2\pi \xi )\operatorname {rect} (\pi \xi )}{\sqrt {1-4\pi ^{2}\xi ^{2}}}}$	${\sqrt {\frac {2}{\pi }}}{\frac {(-i)^{n}T_{n}(\omega )\operatorname {rect} \left(\displaystyle {\frac {\omega }{2}}\right)}{\sqrt {1-\omega ^{2}}}}$	${\frac {2(-i)^{n}T_{n}(\nu )\operatorname {rect} \left(\displaystyle {\frac {\nu }{2}}\right)}{\sqrt {1-\nu ^{2}}}}$	315の一般化。Jn (x ) はn 次の第1種ベッセル関数、Tn (x ) は第1種チェビシェフ多項式。

二変数函数

	もとの函数	ユニタリ・周波に関するフーリエ変換	ユニタリ・角周波に関するフーリエ変換	非ユニタリ・角周波に関するフーリエ変換	備考
	$f(x,y)$	${\hat {f}}(\xi _{x},\xi _{y})=$ $\iint f(x,y)e^{-2\pi i(\xi _{x}x+\xi _{y}y)}\,dxdy$	${\hat {f}}(\omega _{x},\omega _{y})=$ ${\frac {1}{2\pi }}\iint f(x,y)e^{-i(\omega _{x}x+\omega _{y}y)}\,dxdy$	${\hat {f}}(\nu _{x},\nu _{y})=$ $\iint f(x,y)e^{-i(\nu _{x}x+\nu _{y}y)}\,dxdy$	ξx , ξy , ωx , ωy , νx , νy は実変数。積分領域は全平面である。
401	$e^{-\pi \left(a^{2}x^{2}+b^{2}y^{2}\right)}$	${\frac {1}{|ab|}}e^{-\pi \left(\xi _{x}^{2}/a^{2}+\xi _{y}^{2}/b^{2}\right)}$	${\frac {1}{2\pi \cdot |ab|}}e^{\frac {-\left(\omega _{x}^{2}/a^{2}+\omega _{y}^{2}/b^{2}\right)}{4\pi }}$	${\frac {1}{|ab|}}e^{\frac {-\left(\nu _{x}^{2}/a^{2}+\nu _{y}^{2}/b^{2}\right)}{4\pi }}$	両方のガウス関数は規格化されている必要はない。
402	$\mathrm {circ} ({\sqrt {x^{2}+y^{2}}})$	${\frac {J_{1}\left(2\pi {\sqrt {\xi _{x}^{2}+\xi _{y}^{2}}}\right)}{\sqrt {\xi _{x}^{2}+\xi _{y}^{2}}}}$	${\frac {J_{1}\left({\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}\right)}{\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}}$	${\frac {2\pi J_{1}\left({\sqrt {\nu _{x}^{2}+\nu _{y}^{2}}}\right)}{\sqrt {\nu _{x}^{2}+\nu _{y}^{2}}}}$	元の函数は circ(r ) = 1 (0≤r ≤1), and 0 (otherwise) で定義される。これはエアリー分布であり、1次の第1種ベッセル函数 J1 で表される。

一般の n-変数函数

	もとの函数	ユニタリ・周波に関するフーリエ変換	ユニタリ・角周波に関するフーリエ変換	非ユニタリ・角周波に関するフーリエ変換	備考
	$f(x)\,$	${\hat {f}}(\xi )=$ $\int _{\mathbb {R} ^{n}}f(x)e^{-2\pi ix\cdot \xi }\,dx$	${\hat {f}}(\omega )=$${\frac {1}{{(2\pi )}^{(n/2)}}}\int _{\mathbb {R} ^{n}}f(x)e^{-i\omega \cdot x}\,dx$	${\hat {f}}(\nu )=$ $\int _{\mathbb {R} ^{n}}f(x)e^{-ix\cdot \nu }\,dx$
501	$\chi _{[0,1]}(|x|)(1-|x|^{2})^{\delta }\,$	$\pi ^{-\delta }\Gamma (\delta +1)|\xi |^{-(n/2)-\delta }\,$ $\cdot J_{n/2+\delta }(2\pi |\xi |)$	$2^{-\delta }\Gamma (\delta +1)\left|\omega \right|^{-(n/2)-\delta }$ $\cdot J_{n/2+\delta }(|\omega |)$	$\pi ^{-\delta }\Gamma (\delta +1)\left|{\frac {\nu }{2\pi }}\right|^{-(n/2)-\delta }$ $\cdot J_{n/2+\delta }(|\nu |)$	χ[0,1] は区間 [0, 1] の指示関数、Γ(x ) はガンマ関数、Jn /2+δ はn /2 + δ次の第1種ベッセル関数である。n = 2 およびδ = 0とすると402を得る。

関連項目

• フーリエ級数
• フーリエ級数の収束
• フーリエ解析
• 微分方程式
• 高速フーリエ変換
• ラプラス変換
• 離散フーリエ変換
  • DFT行列
• 離散時間フーリエ変換
• 分数階フーリエ変換
• 線型正準変換
• フーリエ正弦変換
• 短時間フーリエ変換
• 量子フーリエ変換
• アナログ信号処理
• 変換 (数学)
• 擬微分作用素
• フーリエ–ドリーニュ変換
• フーリエ–向井変換
• フーリエ–佐藤変換
• 量子フーリエ変換 (量子群)

参考文献

• Bochner, S.; Chandrasekharan, K. (1949). Fourier Transforms. Princeton University Press 
• Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill .
• Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc. .
• Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5 .
• Dym, H; McKean, H (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0122264511 .
• Erdélyi, Arthur, ed. (1954), Tables of Integral Transforms, 1, New Your: McGraw-Hill 
• Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 0-13-035399-X .
• Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer-Verlag, ISBN 978-3540006626 .
• James, J.F. (2002), A Student's Guide to Fourier Transforms (2nd ed.), New York: Cambridge University Press, ISBN 0-521-00428-4 .
• Kaiser, Gerald (1994), A Friendly Guide to Wavelets, Birkhäuser, ISBN 0-8176-3711-7 
• Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 0-13-578782-3 
• Katznelson, Yitzhak (1976), An introduction to Harmonic Analysis, Dover, ISBN 0-486-63331-4 
• Bao Luong（2009): Fourier Analysis on Finite Abelian Groups, Birkhäuser, ISBN 978-0-8176-4916-6. ※ 有限アーベル群上のフーリエ解析
• Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6 
• Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 0-8493-2876-4 .
• Dinakar Ramakrishnan,and Robert J. Valenza (1999): Fourier Analysis on Number Fields, Springer (GMT 186),ISBN 978-1-4757-3085-2. ※ 数論関連
• Rudin, Walter (1987), Real and Complex Analysis (Third ed.), Singapore: McGraw-Hill, ISBN 0-07-100276-6 .
• Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 0-691-11384-X .
• Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9 .
• Audrey Terras (1999): Fourier Analysis on Finite Groups and Applications,　Cambridge University Press, ISBN 978-0-52145718-7. ※ 有限群上のフーリエ解析
• Wilson, R. G. (1995), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, ISBN 0471303577 .
• Yosida, K. (1968), Functional Analysis, Springer-Verlag, ISBN 3-540-58654-7 .

関連図書

• 高橋洋一郎：「実関数とフーリエ解析」、岩波書店、ISBN 4-00-005457-0 (2006年7月7日).

外部リンク

• Fourier Series Applet (Tip: drag magnitude or phase dots up or down to change the wave form).
• Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.
• Weisstein, Eric W. “Fourier Transform”. mathworld.wolfram.com (英語).
• Fourier Transform Module by John H. Mathews
• The DFT “à Pied”: Mastering The Fourier Transform in One Day at The DSP Dimension
• FFT in Python
• Fourier-transform (mathematics) - ブリタニカ百科事典
• 日本大百科全書(ニッポニカ)『フーリエ変換』 - コトバンク