複素数

数学における
- z = a + bi
と表すことのできる数のことである[注釈 1]。1, i は実数体上線型独立であり、複素数は、係数体を実数とする、1, i の線型結合である。実数体 R 上の二次拡大環の元であるため、二元数の一つである。
複素数全体からなる集合を、太字の C あるいは黒板太字で ℂ と表す。C は可換体である。体論の観点からは、複素数体 C は、実数体 R に √−1 を添加して得られる体の拡大である。代数学の基本定理により、複素数体は代数的閉体である。
複素数体はケーリー=ディクソン代数(四元数、八元数、十六元数など)の基点となる体系であり、またさまざまな多元数の中で最もよく知られた例である。
複素数の概念は、一次元の実数直線を二次元の複素平面に拡張する。複素数全体に通常の大小関係を入れることはできない[5][6]。つまり、複素数体 C は順序体でない[注釈 2]。
数学での分野、概念や構成において、考えている体構造が複素数体であるとき、それを、それらの概念等の名称に、多くは接頭辞「複素-」を付けることで反映させる。例えば、複素解析、複素行列、複素(係数)多項式、複素リー代数など。
概観[編集]
定義[編集]
i2 = −1 を満たす数 i を虚数単位という。実数 1 と i は実数体上で線型独立である。実数 a, b を係数として 1, i の線型結合で表される数 a + bi を複素数と呼ぶ[注釈 3]。
任意の実数 a は a + 0i と表せるので複素数である(実数全体の複素数全体への埋め込みは、四則演算および絶対値を保つという意味で、位相体の埋め込みである)。bi = 0 + bi (b ≠ 0) の形の複素数を純虚数と呼ぶ。
複素数 z = a + bi (a, b ∈ R) に対して、
- a を z の実部 (real part) といい、Re(z), ℜ(z), Re z, ℜ z などで表す。
- b を z の虚部 (imaginary part) といい、Im(z), ℑ(z), Im z, ℑ z などで表す。虚部とは実数「b」を指し複素数「bi」ではないことに注意[7][8]。
- 虚部が 0 でない、すなわち実数でない複素数のことを虚数という。
- 実部、虚部がともに整数のときガウス整数といい、その全体を Z[i] と書く。
- 実部、虚部がともに有理数のときガウス有理数といい、その全体を Q(i) と表す。
複素平面[編集]

複素数 z = x + iy(x, y は実数)は実数の対 (x, y) に 1: 1 に対応するから、複素数全体からなる集合 C は、z = x + iy を (x, y) と見なすことにより座標平面と考えることができる。この座標平面を複素平面という。カール・フリードリヒ・ガウスに因んでガウス平面、ジャン゠ロベール・アルガンに因んでアルガン図と呼ばれることもある。これと異なる語法として、C は複素数体上一次元のアフィン線型多様体であるので、複素直線とも呼ばれる。
複素数平面においては、x座標が実部、y座標が虚部に対応し、x軸(横軸)を実軸 (real axis) 、y軸(縦軸)を虚軸 (imaginary axis) と呼ぶ[9]。
複素数 z, w に対して
- d(z, w) = |z − w|
とすると、(C, d) は距離空間となる。この距離は、座標平面におけるユークリッド距離に対応する。複素数平面は複素数の計算を視覚化でき、数直線の概念そのものを拡張した。
複素数球面[編集]
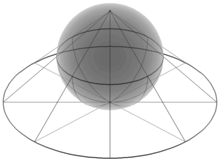
複素関数論においては、複素数平面 C を考えるよりも、無限遠点を付け加えて1点コンパクト化した C ∪ {∞} を考える方が自然であり、議論が透明になることもある。複素数球面またはリーマン球面と呼ばれ、以下に示すように2次元球面同型 S2 と位相同型である。無限遠点にも幾何的な意味を与えることができる。
複素数平面 C を、xyz座標空間内の xy平面とみなし、z ≥ 0 に含まれ xy平面と原点で接する球面 x2 + y2 + (z − 1)2 = 1 を考える。この球における原点の対蹠点 (0, 0, 2) を北極と呼ぶことにする。任意の複素数 w に対し w と北極を結んだ線分はこの球面と、北極以外の一点で必ず交わり、それを f(w) と書けば f は単射、連続写像である。f の像は、球面から北極を除いた部分である。また、w → ∞ のとき f(w) → (0, 0, 2)(北極)である。そこで、f の定義域を C ∪ {∞} に拡張すると、f : C ∪ {∞} → S2 は同相写像になる。
この同相写像 f は、複素平面上の円を円に写し、複素平面上の直線を、無限遠点を通る円に写す。このことは、複素平面上の直線と円はほぼ同等であることを表している。
基本的な性質[編集]
相等関係[編集]
二つの複素数が等しいとは、それらの実部および虚部がそれぞれ等しいことである:
このことは、1, i が線型独立であることから示される。
四則演算[編集]
- (a + bi) ± (c + di) = (a ± c) + (b ± d)i(複号同順)
- (a + bi)(c + di) = (ac − bd) + (bc + ad)i
n, m は整数とする。
- znzm = zn+m
- (zn)m = znm
- (zw)n = znwn
複素共役(共役複素数)[編集]

複素数 a + bi に対して、虚部 b を反数にした複素数 a − bi を z の共役(きょうやく、conjugate, 本来は共軛)複素数といい、記号で z(または z*)と表す[9]。
- z = Re z − i Im z
z と z を複素共役あるいは単に共役という。
複素数の共役をとる複素関数 ・ : C → C ; z ↦ z は環準同型である。すなわち次が成り立つ。
- z + w = z + w
- zw = z w
複素共役は実数を変えない:
- z が実数 ⇔ z = z
逆に、C 上の環準同型写像で、実数を変えないものは、恒等写像か複素共役変換に限られる。
複素共役変換 ・ : C → C ; z ↦ z は、C の全ての点で複素微分不可能である。
以下の性質が成り立つ。
- z が実数 ⇔ z = z
- z が純虚数 ⇔ z = −z ≠ 0
- z ± w = z ± w(複号同順)
- zw = z w
- (n は整数)
- (対合)
- |z| = |z|
- zz = |z|2
- z + z = 2 Re z
- z − z = 2i Im z
代数方程式の解について、次が成り立つ:
- 「実係数多項式 P(x) が虚数根 α をもつならば、α も P(x) の虚数根である」
つまり、
- 実係数多項式 P(x) について、P(α) = 0 ⇔ P(α) = 0
- (1746年、ダランベール)
このことは、複素共役変換が環準同型であることから容易に示せる。
極形式[編集]

z = r(cos φ + i sin φ) あるいは reiφ
で与えられる。
複素数を実部と虚部で表すのとは別の方法として、複素数平面上での点 P を、原点 O(0) からの距離と、正の実軸と線分 OP の見込む角を反時計回りに測ったものの対(P の極座標)で表す方法が挙げられる。これにより、複素数の極形式の概念が導入される。
絶対値[編集]
複素数 z = x + yi(x, y は実数)の絶対値は
で定義される。これは 0 以上の実数である。z が実数(つまり y = 0)のとき |z| は実数の絶対値 |x| = max{x, −x} に一致する。
複素数の絶対値は、ピタゴラスの定理により、複素平面における原点 O(0) とのユークリッド距離に等しい。そして次が成り立つ。
逆に、複素数の絶対値は、実数の絶対値を複素数に拡張したノルム代数として特徴付けられる。
複素数 z の絶対値 |z| は、z を極形式表示:
- z = r(cos θ + i sin θ)
したときの動径 r に等しい。
共役複素数と自身の積は、絶対値の平方に等しい。すなわち複素数 z に対して
が成り立つ。
偏角[編集]
複素数 z の偏角(応用の場面ではしばしば「位相」とも呼ばれる)arg z とは、複素平面上で、正の実軸から測った動径 OP の角度のことである。偏角 φ の値はラジアンで表すものとする。
角に 2π の任意の整数倍を加えてもそれが表す動径、複素数は同じであるから、偏角を与える関数は多価関数である。
そこで、偏角 arg z を一価関数として定義するには、主値を区間 (−π, π] とする場合、逆正接関数から次のようにして定義される[11](計算機言語では、y/x の逆正接関数を、二つの引数 x, y に対する atan2(y, x) として実装していることが多い):
複素数が 0 のときだけ偏角は不定 (indeterminate) となる。
上記の定義で、負となる偏角の値に対しては 2π を加えることにすると、主値は [0, 2π) となる。
複素数 z が主値の端の値の近傍を連続的に変化するならば、偏角の値もまたその近傍で連続的に変化するように枝をとるものとして、それを単に arg z = arctan y/x のように書く[注釈 5]。
極形式の表示と記法[編集]
複素数 z = x + yi(x, y は実数)において、直交座標系 (x, y) に対応する極座標系を (r, φ) (r ≥ 0) とするとき、
- (三角関数表示)
と表すことができる。この表示式を極形式 (polar form) という。r は z の絶対値、φ は z の偏角である。0 を除いて、この表示は一意である。
極形式から元の直交座標を恢復するには、三角関数表示を展開すればよい。
オイラーの公式を用いれば、これを
- z = reiφ
と書くことができるし、純虚指数函数を用いて
- z = r cis(φ)
と書くこともある。
は電子工学において振幅 r と位相 φ を持つ正弦信号を表すのによく用いられる[12]。
極形式表示での乗除法[編集]

赤三角は、青三角の偏角だけ回転され、青三角の斜辺 (√5) は、赤三角の斜辺だけ拡大され
(2 + i)(3 + i) = 5 + 5i
を表す三角(灰)になる。
5 + 5i の偏角は π/4(ラジアン)であるから、偏角について
π/4 = arctan 1/2 + arctan 1/3
が成り立つ(arctan は逆正接関数)。逆正接関数は高効率で近似することができることに応じて、π を高精度に近似するこのような式(マチンの公式と呼ばれる)に用いられる。
複素数の乗除・冪は、極形式表示をしてから行う方が、直交座標表示よりも、見通しがよくなる。2つの複素数の極形式を
- z1 = r1(cos φ1 + i sin φ1),
- z2 = r2(cos φ2 + i sin φ2)
とすると、積 z1 z2 は、三角関数の加法定理:
により
となる。すなわち、積の絶対値は絶対値の積であり、積の偏角は偏角の和である。
i2 = −1 より、虚数単位 i = √−1 を掛けること(作用)は、複素数平面上で原点中心に反時計回りに直角回転させることである。ゆえに、虚数単位 i は、複素数平面上では、直交座標で (0, 1) の位置にある。
同様にして、商は
になる。
偏角の計算規則[編集]
偏角に関する等式 arg(zw) = arg(z) + arg(w) は、両辺の差が 2π の任意の整数倍であることを除いて成り立つ等式であることに注意しなければならない。
- 例えば
- arg(z2) = arg(z) + arg(z) = 2 arg(z)
- において、もし各項が任意の偏角をとるものとしてしまうと、
- arg(z) = θ + 2nπ(n は任意の整数)
- と書けば、右辺は 2θ + 4nπ だが左辺は 2θ + 2mπ(m は任意の整数)となり厳密には等しくならない。
それを明示するために合同式の記法を流用してしばしば
- arg(zw) ≡ arg(z) + arg(w) (mod 2π)
などとも書く。このように mod 2π に関して合同であるという理解は重要である。しかし、先述のように(適当なリーマン面上で)偏角をとるものと仮定すれば、2π の整数倍を加える不定性無く実際に等号が成り立つ。すなわち、三つの複素数 zw, z, w のそれぞれに対して独立に偏角をとるのではなく、ひとたび arg(zw) = arg(z) + arg(w) を満たすように偏角を一組選べば(例えば右辺の各項の値を決め、それによって左辺の値を定義すれば)、z あるいは w を連続的に変化させるとき、arg(zw) も連続的に変化して、そのような三点の近傍において常に厳密な意味で等号が成立する[13]。
この注意の下で以下が成り立つ:
- arg(zw) = arg(z) + arg(w)
- arg(z/w) = arg(z) − arg(w)
- arg(zn) = n arg(z)(n は整数)
偏角の計算法則は対数のそれとほぼ同じであるが、それは複素対数函数の虚部が偏角に等しいことに起因している。
ド・モアブルの定理[編集]
実数 θ, 整数 n に対して、
- (cos θ + i sin θ)n = cos nθ + i sin nθ
が成り立つ(ド・モアブルの定理)。オイラーの公式より
- (eiθ)n = einθ
- (exp iθ)n = exp inθ
と表現することもできる。n が整数でないとき一般には成り立たない。
性質と特徴付け[編集]
体構造[編集]
複素数全体からなる集合 C は可換体になる。つまり、以下の事実が成り立つ。
- 閉性:任意の二つの複素数の和および積は再び複素数になる。
- 反数の存在:任意の複素数 z に加法逆元 −z が存在してそれもまた複素数である。
- 逆数の存在:任意の非零複素数に対して乗法逆元 1/z が存在する。
- さらにいくつかの法則を満足する。複素数 z1, z2, z3 に対して
これらの性質は、実数全体からなる集合 R が可換体であるという事実の下、先に与えた基本的な和と積の定義式から証明することができる。
実数と異なり、虚数に通常の大小関係 (z1 < z2) はない。つまり、複素数体 C は順序体にはならない[5][9]。これは、自乗すると負である数(例えば虚数単位 i)が存在することによる。
代数的閉体[編集]
代数学の基本定理より、複素数を係数とする代数方程式の解は存在しまた複素数になる。つまり、
は、少なくとも一つの複素根 z を持つ。
上記の多項式の複素根の一つを α1 とし、因数定理を帰納的に用いると、上記の多項式は
と複素数の範囲で因数分解される。これは、複素数が代数方程式による数の拡張の最大であることを意味している。つまり、C は代数的閉体である。
代数学の基本定理の証明にはさまざまな方法がある。例えばリウヴィルの定理などを用いる解析的な方法や、巻き数などを使う位相的な証明、あるいは奇数次の実係数多項式が少なくとも一つの実根を持つ事実にガロア理論を組み合わせた証明などがある。
この事実により、「任意の代数的閉体に対して成り立つ定理」を C にも適用できる。例えば、任意の空でない複素正方行列は少なくとも一つの複素固有値を持つ。
代数的特徴付け[編集]
体 C は以下の三つの性質:
- 標数は 0 である。これは 1 を何回足しても 1 + 1 + … + 1 ≠ 0 となるという意味である。
- C の素体 Q 上の超越次数は連続体濃度に等しい。
- 代数的閉体である。(#代数的閉体を参照)
を満足する。この三つの性質を持つ任意の体は、体として C に同型であることが示せる。例えば Qp の代数的閉包はこれら三つを満たすので、C に同型となる。この代数的な C の特徴付けの帰結として、C は自身に同型な真の部分体を無数に含むことが分かる。
また C は複素ピュイズー級数体に同型である(が、その同型を決めるには選択公理が必要となる)。
位相体としての特徴付け[編集]
C には代数的側面のみならず、近傍や連続性などの解析学や位相空間論の分野で考慮の対象となる性質も備わっている。そのような位相的性質に関して C は、適当な意味で収束の概念を考えることのできる位相体を成すことに注意しよう。
C は以下の三条件を満たす部分集合 P を持つ。
- P は加法、乗法および逆元を取ることについて閉じている。
- P の異なる元 x, y に対して、x − y または y − x のうちの何れか一方のみが P に属する。
- S が P の空でない部分集合ならば、適当な x ∈ C に対して S + P = x + P が成り立つ。
この P はつまり正の実数全体の成す集合である。さらに言えば、C は非自明な対合的反自己同型として複素共軛変換 x ↦ x* を持ち、任意の非零複素数 x に対して xx* ∈ P が成り立つ。
これらの性質を満たす任意の体 F には、任意の x ∈ F, p ∈ P に対する集合 B(x, p) = { y | p − (y − x)(y − x)* ∈ P} を開基とすることによって、位相を入れることができ、この位相に関して F は C に位相体として同型になる。
これとは別の位相的な特徴付けに、連結な局所コンパクト位相体は R および C に限ることが利用できる。実際このとき、非零複素数の全体 C ∖ {0} は連結だが、非零実数の全体 R ∖ {0} は連結でないという事実を併せれば、R と峻別することができる。
乗法群の構造[編集]
非零複素数の全体 C* = C ∖ {0} は、複素数体 C の乗法群 C× であり、C における距離空間としての部分位相空間と見て、位相群を成す。また、絶対値 1 の複素数全体の成す群(円周群)U はその部分位相群であり、写像
および写像
は位相群としての同型である。ここに、R/Z は商位相群、R∗
+ は正の実数の全体が乗法についてなす群であり、× は位相群の直積を表す。
形式的構成[編集]
実数の対として[編集]
1835年にハミルトンによって、負の数の平方根を用いない複素数の定義が与えられた。
実数の順序対 (a, b) および (c, d) に対して和と積を
- (a, b) + (c, d) = (a + c, b + d)
- (a, b) × (c, d) = (ac − bd, ad + bc)
により定めるとき、(a, b) を複素数という。実数 a は (a, 0) で表され、虚数単位 i は (0, 1) に当たる。このとき、R2 は +, × に関して体となり、零元は (0, 0)、単位元は (1, 0) である[14]。
ハミルトンの代数的な見方に対するこだわりは、複素数をさらに拡張した四元数の発見へと結び付いた。
剰余環としての構成[編集]
複素数体 C の代数的な構造は、体および多項式の概念により、自然に構成することができる。
体とは、四則演算ができてよく知られた計算法則を満たすものである(例えば有理数体など)。実数全体の成す集合 R は体である。また、係数体が R の多項式全体の成す集合 R[X] は、通常の加法、乗法に関して環を成す(多項式環と呼ばれる)ことに注意する。
剰余環 R[X]/(X2 + 1) は、R を含む体であることは示すことができる。この拡大体において、X, −X(の属する剰余類)は −1 の平方根である。この剰余環の任意の元は、多項式の除法の原理より、a + bX(a, b は実数)の形の多項式を代表元に一意に持つ。ゆえに、R[X]/(X2 + 1) は R 上の2次元ベクトル空間であり、(1, X)(が属する剰余類)はその基底である。
R[X]/(X2 + 1) の元(剰余類)a + bX(a, b は実数)を、実数の順序対 (a, b) に対応させると、前節で述べた体が得られる。この2つの体は体同型である。
行列表現[編集]
複素数 α = a + bi を、C 上の(左からの)作用と見ると、それに対応する R2 上での一次変換の表現行列を考えることができる。
対応
により、複素数は実二次正方行列で表現することができる。特に、実数単位 1, 虚数単位 i は
である。この対応により、複素数の加法および乗法は、この対応によって通常の行列の和および行列の乗法に対応する。複素共役は転置行列に対応している。
極形式表示を a + bi = r(cos θ + i sin θ) とすると、
は角度 θ の回転行列のスカラー r 倍であり、これは複素数の積が R2 上で原点を中心とする相似拡大と回転の合成を引き起こすことに対応する。
複素数 z = a + bi の表現行列を A とすると、A の行列式
- det A = a2 + b2 = |z|2
は対応する複素数の絶対値の平方である。
複素数のこの行列表現はよく用いられる標準的なものだが、虚数単位 i に対応する行列 を例えば に置き換えても、平方が単位行列の −1 倍であり、複素数の別の行列表現が無数に考えられる(後述、また実二次正方行列の項も参照)。
複素函数[編集]

複素変数の函数の研究は複素解析と呼ばれ、純粋数学の多くの分野のみならず応用数学においても広汎な応用がもたれる。実解析や数論等における命題の最も自然な証明が、複素解析の手法によって為されることもしばしば起こる(例えば素数定理。あるいは代数学の基本定理のルーシェの定理による証明)。実函数が一般に実二次元のグラフとして視覚的に理解することができたのとは異なり、複素函数のグラフは実四次元となるから、その視覚化に際しては二次元や三次元グラフに色相(もしくは明度や彩度、輝度)による次元を加えたり、あるいは複素函数の引き起こす複素数平面の動的な変換をアニメーションで表したりすることが有効になる。
実解析における収束級数や連続性などの概念は、いわゆるε-δ論法において実数の絶対値を用いたところを複素数の絶対値で置き換えることにより、複素解析においても自然に考えられる。例えば、複素数列が収束するための必要十分条件は、その実部および虚部の成す実数列がともに収束することである。もう少し抽象的な観点では、C は距離函数
が成立する。実解析と同様に、収束の概念はいくらかの初等関数の構成において用いられる。
指数・対数[編集]
複素指数函数[編集]
で定義される。この級数の収束半径は ∞ であるから、複素指数函数は C 上正則関数(整関数)である。
任意の実数 φ に対して次の等式が成り立つ:
- (オイラーの公式)
一般の複素変数 z に拡張した余弦函数 cos z, 正弦函数 sin z は次の式で定義できる:
余弦函数、正弦函数は整関数である。整関数であるような拡張の仕方は、一致の定理より一意である。
cosh, sinh などの双曲線関数も、同様に複素指数函数により定義できる。
複素対数函数[編集]
実函数の場合と異なり、複素数 z に関する方程式
は任意の非零複素数 w に対して無限個の複素数解を持つ。そのような解 z、すなわち w の複素対数函数 log w は
と表すことができる。ただし、ln は実函数としての自然対数で、arg は上述の偏角である。この値は、偏角のときと同様に 2π の整数倍の差を除いて一意であるから、複素対数函数もまた多価関数の主値としては、虚部 arg w を区間 (−π, π] にすることが多い。
複素数の複素数乗[編集]
複素数の複素数乗 zω は
として定義される。対数函数は多価であったから、その結果として複素数の複素数乗も一般には多価になる。特に ω = 1/n(n は自然数)の形のときは、複素数 z の n乗根 n√z を表し、値は一意に定まらない。
対数函数の適当な枝をとって一価函数として扱うとき、実数の実数乗に対して成立していた指数法則や対数法則は、複素数の複素数乗では一般に成り立たない。例えば、
は a, b, c が複素数である場合には一般には成立しない。この式の両辺を今述べたような多価の値を持つものと見なす場合、左辺の値の全体は右辺の値の全体の成す集合の部分集合になっていることに注意する。
正則函数[編集]
D を複素数平面 C の領域とする。
複素函数 f : D → C が正則であるとは、定義域 D の各点で複素微分可能であることである。実部と虚部に分けて考えると、f が正則である必要十分条件は、Re f, Im f が微分可能で、コーシー・リーマンの方程式を満たすことである。例えば、複素函数
や
は正則でない。これらはコーシー・リーマンの方程式を満たさず複素微分可能でない。
複素解析には実解析に無いいくつかの特徴がある。
正則函数は解析関数である(正則関数の解析性)。したがって、正則函数は何回でも微分可能である。
2つの正則函数 f, g が D のある小さな、正則曲線上で一致するならば、それらは全体でも一致する(一致の定理、解析接続)。
有理型関数は、局所的には正則函数 f を用いて f(z)/(z − z0)n で近似でき、正則函数といくつかの特徴が共通する。有理型でない函数は真性特異点をもつ(例えばsin 1/z は z = 0 で真性特異点を持つ)。
歴史[編集]
負の数の平方根について、いささかなりとも言及している最も古い文献は、数学者で発明家のアレクサンドリアのヘロンによる『測量術』(Stereometrica) である。そこで彼は、現実には不可能なピラミッドの錐台について考察しているものの、計算を誤り、不可能であることを見逃している。
16世紀にイタリアの数学者カルダーノやボンベリによって三次方程式の解の公式が考察され、特に相異なる 3 個の実数解を持つ場合に解の公式を用いると、負の数の平方根を取ることが必要になることが分かった。当時は、まだ、負の数でさえあまり認められておらず、回避しようと努力したが、それは不可能なことであった。
17世紀になりルネ・デカルトによって、虚 (imaginary) という言葉が用いられ、虚数と呼ばれるようになった。デカルトは作図の不可能性と結び付けて論じ、虚数に対して否定的な見方を強くさせた。
その後、ウォリスにより幾何学的な解釈が試みられ、ヨハン・ベルヌーイやオイラー、ダランベールらにより、虚数を用いた解析学、物理学に関する研究が多くなされた。
複素平面が世に出たのは、1797年にノルウェーの数学者カスパー・ベッセル (Caspar Wessel) によって提出された論文が最初とされている。しかしこの論文はデンマーク語で書かれ、デンマーク以外では読まれずに1895年に発見されるまで日の目を見ることはなかった。1806年にジャン=ロベール・アルガン (Jean-Robert Argand) によって出版された複素平面に関するパンフレットは、ルジャンドルを通して広まったものの、その後、特に進展は無く忘れられていった。
1814年にコーシーが複素解析を始め、複素数を変数に取る解析関数や複素線積分が論じられるようになった[15]。
1831年に、機は熟したと見たガウスが、複素平面を論じ、複素平面はガウス平面として知られるようになった[16]。ここに、虚数に対する否定的な視点は完全に取り除かれ、複素数が受け入れられていくようになる。実は、ガウスはベッセル(1797年)より前の1796年以前にすでに複素平面の考えに到達していた。1799年に提出されたガウスの学位論文は、今日、代数学の基本定理と呼ばれる定理の証明であり[17]、複素数の重要な特徴付けを行うものだが、複素数の概念を表に出さずに巧妙に隠して論じている[16]。
他分野における複素数の利用[編集]
複素数 A と実数 ω により定まる、一変数 t の関数 Aeiωt は時間 t に対して周期的に変化する量を表していると見なすことができる。周期的に変化し、ある種の微分方程式を満たすような量を示すこのような表示はフェーザ表示と呼ばれ、電気・電子工学における回路解析や、機械工学・ロボット工学における制御理論、土木・建築系における振動解析で用いられている[18]。
物理学[編集]
物理における振動や波動など、互いに関係の深い2つの実数の物理量を複素数の形に組み合わせて表現すると便利な場面が多いため、よく用いられる。
量子力学では複素数が本質的である(数学的定式化に用いられる)。物体の位置と運動量とはフーリエ変換を介して同等の扱いがなされ、波動関数たちのなす複素ヒルベルト空間とその上の作用素たちが理論の枠組みを与える。
複素数の拡張[編集]
複素数とは実数体上の、実数単位 1, 虚数単位 i の線型結合であるが、これに新たな単位を有限個加えて可換体(通常の四則演算ができる数の体系)を作ることはできない[19][20]。実数体 R から拡張して C を得る過程はケーリー=ディクソンの構成法と呼ばれる。この過程を推し進めると、より高次元の四元数体 H, 八元数体 O が得られる。これらの、実数体上の線形空間としての次元はそれぞれ 4, 8 である。この文脈において複素数は「二元数」(binarions) とも呼ばれる[21]。
注意すべき点として、実数体にケーリー=ディクソンの構成を施したことにより、順序に関する性質が失われていることである。より高次元へ進めば実数や複素数に関してよく知られた性質が失われていくことになる。四元数は唯一の非可換体であり[19][20](つまり、ある二つの四元数 x, y に対して x·y ≠ y·x となる)、八元数では(非可換なばかりでなく)乗法に関する結合法則も失われる(つまり、ある八元数 x, y, z に対して (x⋅y)⋅z ≠ x⋅(y⋅z) となる)。一般に、実数体 R 上のノルム多元体は、同型による違いを除いて、実数体 R, 複素数体 C, 四元数体 H, 八元数体 O の4種類しかない(フルヴィッツの定理)[22]。ケーリー=ディクソン構成の次の段階で得られる十六元数環ではこの構造は無くなってしまう。
ケーリー=ディクソン構成は、C(を R-線型環、つまり乗法を持つ R-線型空間と見て)の正則表現と近しい関係にある。すなわち、複素数 w に対して、R-線型写像 fw を
とすると、fw の(順序付き)基底 (1, i) に関する表現行列は、実二次正方行列
である(つまり、#行列表現で述べた行列に他ならない)。これは C の標準的な線型表現だが、唯一の表現ではない。実際、
なる形の任意の行列はその平方が単位行列の −1 倍、すなわち J2 = −I を満たすから、行列の集合
もまた C に同型となり、R2 上に別の複素構造を与える。これは線型複素構造の概念によって一般化することができる。
多元数は R, C, H, O もさらに一般化するもので、例えば分解型複素数環は剰余環 R[x]/(x2 − 1) である(複素数は剰余環 R[x]/(x2 + 1) であった)。この環において方程式 a2 = 1 は4つの解を持つ。
実数体 R は有理数体 Q の通常の絶対値による距離に関する完備化である。Q 上の別の距離函数をとれば、任意の素数 p に対して p進数体 Qp が導かれる(つまりこれは実数体 R の類似対応物である)。オストロフスキーの定理によれば、この R と Qp 以外に Q の非自明な完備化は存在しない。Qp の代数的閉包 Qp にもノルムは伸びるが、C の場合と異なり、そのノルムに関して Qp は完備にならない。Qp の完備化 Cp は再び代数的閉体であり、C の類似対応物として p-進複素数体と呼ぶ。
体 R, Qp およびそれらの有限次拡大体は、すべて局所体である。
脚注[編集]
注釈[編集]
- ^ ガウスは、1831年[1]に発表した論文で、複素数を 独: "Komplexe Zahl"(「複合的な数」)と表し、初めて複素数に名前を付けた[2][3]。
英: "Complex number" を最初に「複素数」と訳したのは、日本の藤沢利喜太郎である[4]。1889年の著書『数学用語英和対訳字書』[1] p.7 による。(ただし、東京数学会社による、"Composite number"(合成数)の日本語訳「複素数」も見られる) - ^ 辞書式順序は全順序であるが、複素数に入れると +, × と両立しない。
「順序集合」を参照
- ^ 1 と実数体上線型独立なベクトル u が u2 = 1 or 0 となるものとすれば、別の種類の二元数が得られる。
- ^ 複素数を拡張した四元数では、逆数はこの式で定義される[10]。
- ^ これは正確には適当なリーマン面を考えるべきであろうけれども、直観的には tan(arctan(α)) = α かつ arctan(tan(β)) = β が常に成り立っているように枝を渡る(特定の一つの枝を固定したのでは不連続となる点の前後で、実際には隣の枝に遷る)と理解することができる。
出典[編集]
- ^ なぜ虚数単位iの2乗は-1になるのか?#6.3.3. 複素数の由来 x_seek
- ^ 複素数 2006/10/05 (PDF) 矢崎成俊 p.3
- ^ 複素平面の基本概念 (PDF) p.3
- ^ 片野善一郎『数学用語と記号ものがたり』裳華房、2003年8月25日、63頁。
- ^ a b ニューアクション編集委員会『NEW ACTION LEGEND数学2+B―思考と戦略 数列・ベクトル』(単行本)東京書籍、2019年2月1日、53頁。ISBN 978-4487379927。
- ^ Weisstein, Eric W. "Complex Number". mathworld.wolfram.com (英語).
- ^ Murray Ralph Spiegel 著、石原宗一 訳『複素解析』オーム社〈マグロウヒル大学演習〉、1995年5月。ISBN 978-4274130106。
- ^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007), “Chapter P”, College Algebra and Trigonometry (6 ed.), Cengage Learning, p. 66, ISBN 0-618-82515-0
- ^ a b c 表 (1988)
- ^ 『{{{2}}}』 - 高校数学の美しい物語
- ^ Kasana, H.S. (2005), “Chapter 1”, Complex Variables: Theory And Applications (2nd ed.), PHI Learning Pvt. Ltd, p. 14, ISBN 81-203-2641-5
- ^ Nilsson, James William; Riedel, Susan A. (2008), “Chapter 9”, Electric circuits (8th ed.), Prentice Hall, p. 338, ISBN 0-13-198925-1
- ^ 木村 & 高野 1991, p. 4.
- ^ 高木『解析概論』付録I, §10.
- ^ 高木 (1996, 14. 函数論縁起)
- ^ a b 高木 (1996, pp. 94f.)
- ^ 高木 (1965, §9. 代数学の基本定理)
- ^ なお電気電子工学分野では虚数単位は「j」を用いることが多い(電流(の密度)「i」と混同を避けるため)。
- ^ a b 志賀 (1989, pp. 212–214)
- ^ a b 高木 (1996, pp. 102–116)
- ^ Kevin McCrimmon (2004) A Taste of Jordan Algebras, p.64, Universitext, Springer ISBN 0-387-95447-3 MR2014924
- ^ エビングハウスほか (2012)
参考文献[編集]
- H.D.エビングハウス ほか 著、成木勇夫 訳『数』 下(新装版)、丸善出版〈シュプリンガー数学リーディングス 7〉、2012年9月。ISBN 978-4-621-06387-3。
- 表実『複素関数』岩波書店〈理工系の数学入門コース 5〉、1988年12月8日。ISBN 4-00-007775-9。
- 志賀浩二『複素数30講』朝倉書店、1989年4月10日。ISBN 978-4-254-11481-2。
- 高木貞治『代数学講義』(改訂新版)共立出版、1965年11月25日。ISBN 978-4-320-01000-0。
- 高木貞治『復刻版 近世数学史談・数学雑談』共立出版、1996年12月10日。ISBN 978-4-320-01551-7。
- 木村俊房、高野恭一『関数論』朝倉書店〈新数学講座〉、1991年7月1日。ISBN 978-4-254-11437-9。
関連項目[編集]
外部リンク[編集]
- 『複素数』 - コトバンク
- Weisstein, Eric W. "Complex Number". mathworld.wolfram.com (英語).












































![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)





