因数分解
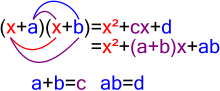
数学における因数分解(いんすうぶんかい、英: factorization, factoring, decomposition[注釈 1]; 分解、因子分解)は、与えられた数学的対象を同種の(しかし普通はより小さいあるいはより平易な)別の対象—それは因数(factor; 因子、乗法因子、乗因子)と呼ばれる—の積として書き表すことを言う[注釈 2]。たとえば、15 という数は 3 × 5 という因数の積に分解され、多項式 x2 − 4 は (x − 2)(x + 2) という因数の積に分解される。
因子への分解は、除法が自由にできる体系(可除環など)ではほとんどの場合に意味を為さない。例えば実数や複素数の体系において任意の x は y が零でない限り何であっても xy × (1/y) のように分解できることは明らかである(つまり、どの元もいくらでも分解できて、積としての表示を無数に持つ)。しかし例えば、有理数や有理関数の成す体系ならば、分子と分母を別々に考えることによって意味のある因数分解を定めることができる。
自然数および整数に関する因数分解は古代ギリシアの数学においてすでに考察されている。その中には、1を除く任意の自然数が素数の積に因数分解できる(さらに、自然数のそのような分解(素因数分解)は因数の順番を変える違いを除いて一通りである)ことを述べた算術の基本定理の証明も含まれる。整数の素因数分解は、整数の乗法のある種の逆演算ではあるけれども、しかしアルゴリズム的な意味(計算量)において乗法とは比べ物にならないほど複雑であり、特に巨大整数の素因数分解は困難な問題で、これを一般に短時間に行う方法は知られていない。この複雑性はRSA暗号のような公開鍵暗号によるセキュリティの信頼性の基礎になっている。
多項式の因数分解もまた何世紀にもわたって研究がおこなわれてきている。初等代数学においては、多項式を因数分解することで多項式の根を求める求根問題を各因子の根を求める問題に帰着させることができる。整数係数の多項式あるいは体に係数をとる多項式の体系は一意分解性質を備えている—それはつまり、(素数を既約多項式に取り換えた)算術の基本定理の多項式版が成り立つということである—。特に、複素数係数の一変数多項式は、必ず一次式の積に(掛ける順番を除いて)一意に表すことができる—これは代数学の基本定理の一つの述べ方である—。この場合、因数分解は求根アルゴリズムが与えられていれば自由にできる。整数係数の場合の多項式の因数分解問題は計算機代数においてひとつの基礎を成す技術的課題である。有理数係数の多項式環における既約因子分解には、効果的な計算機アルゴリズムが存在している。
一般の抽象代数学において、一意分解性質を持つ可換環は一意分解環 (UFD) と呼ばれる。ある種の数体系、例えば代数体の整数環(代数的整数環)の中には一意分解性質を持たないものが存在するが、これら代数的整数環の場合には幸いなことに、より弱い形での一意分解性質(任意のイデアルが素イデアルの積に一意的に分解される)を満足するデデキント環となる。一般に、既約元分解を持つ(が、一意分解とは限らない)整域を原子整域または分解整域と呼ぶ。
より一般の数学的対象の中にも(より単純な対象からなる)積の形に書き表すことを一般に因子分解あるいは分解と言い表すものがある。たとえば、写像の分解とは特定の性質を持つ写像の合成の形に書き表すことである。任意の写像は全射と単射の合成として標準的な分解を持つ(これは圏論において、射の分解系・弱分解系として一般化される)。また例えば、行列の分解とは、与えられた行列を特定の性質を持つ行列を用いて行列の積として書き表すことである。任意の行列は対角成分がすべて 1 の下三角行列 L と上三角行列 U および 置換行列 P の積に分解される(LUP分解: 実はこれはガウスの消去法を行列の形にまとめたものである)。
整数の因数分解[編集]
算術の基本定理により、任意の正の整数は一意的な素因数分解を持つ。整数の因数分解アルゴリズムが与えられたとき、そのアルゴリズムを繰り返し適用して、任意の整数をその構成要素である素数にまで分解しきることができる。しかし、非常に巨大な整数に対して効率のよいアルゴリズムは知られていない。
多項式の因数分解[編集]
因数分解は、方程式や関数について考える上で重要な概念の一つである。たとえば次のように左辺を右辺へ変形することをさす。対して、右辺を左辺へ変形することは展開という。
これらの場合、1. では x − 1 と x − 2 を、2. では t − 1 と t2 − 3 を、3. では α − 1 と α2 + α + 1 をそれぞれ因数と呼ぶ。
係数として用いてよい数の範囲が異なると、因数分解の結果が変わってくる。上の3例はすべて有理数(もしくは整数)の範囲で因数分解を行なったものである。数の範囲を実数まで広げると、2. は更に因数分解が行える。
さらに数の範囲を複素数まで広げると、3. は更に因数分解が行える。
代数方程式 f(x) = 0 に対し、その根を求めることは f(x) を一次式の積に因数分解することと等価である。しかし、展開は機械的に行う方法があるのに対して、整式を因数分解する統一的な方法はないため、状況に応じて適当な方法を適用する必要がある。
共通因数でくくる[編集]
全ての項に共通している因数でくくり出す。たとえば 2x5 − 5x4 = x4(2x − 5) など。
解の公式の利用[編集]
二次方程式の解の公式により、ax2 + bx + c = 0 の解は
であるので
と因数分解される。
例として x2 − x − 2 を因数分解することを考える。 x2 − x − 2 = 0 の解は
である。よって x2 − x − 2 = (x − 2)(x + 1) という因数分解の結果を得る。
2数の和と積[編集]
(x − α)(x − β) = x2 − (α + β)x + αβ という展開を逆向きに使う。x の項の係数と定数項から2数を見つける方法である。
例として x2 − 5x + 6 を因数分解することを考える。x の項の係数が −5 で定数項が 6 なので、和が 5 で積が 6 となる2数を探す。2 と 3 であることが分かるので、x2 − 5x + 6 = (x − 2)(x − 3) という因数分解の結果を得る。
たすきがけ[編集]
2次式を因数分解するときに用いられる、たすきがけとよばれる方法がある。途中計算に引くバツ印の線をたすきの背中側から見た姿になぞらえた名前である。x2 の項の係数の正の約数と定数項の約数を組み合わせて x の項の係数を作る。
たとえば 6x2 + x − 2 を因数分解することを考える。x2 の項の係数 6 の正の約数と定数項 −2 の約数の組み合わせのうち、次のような組み合わせを選ぶ。
この計算で得られた 4 と −3 の和が x の項の係数1と等しいので、× の上の行の数 3 と 2 を使って 3x + 2 という式と作り、同様に下の行の数 2 と −1 を使って 2x − 1 という式を作る。このとき、元の2次式 6x2 + x − 2 はこの2つの式をかけ合わせることで求められるので、6x2 + x − 2 = (3x + 2)(2x − 1) という因数分解の結果を得る。
因数定理の利用[編集]
因数定理を利用する。すなわち f(x) の値を 0 にする x の値(根)を見つける。f(α) = 0 となったとすれば、x − α が f(x) の因数の1つである。
たとえば 2x4 − 5x3 − 8x2 + 17x − 6 を因数分解することを考える。この式に x = 1 を代入すると 0 となるので、x − 1 が因数の1つであることが分かる。元の式を x − 1 で除算して、2x4 − 5x3 − 8x2 + 17x − 6 = (x − 1)(2x3 − 3x2 − 11x + 6) となる。
この方法で求めた1次の因数以外の因数(この例では 2x3 − 3x2 − 11x + 6)は、何らかの方法で更に因数分解できるかもしれない。この例では x = −2 を代入すると 0 になるので x + 2 も因数だと分かる。
因子分解可能な整域[編集]
整数の全体 Z および体 K 上の多項式環 K[X] は一意分解可能—すなわち「零でも単元でもないすべての元が既約元の積に分解される」(例えば整数の場合には、その単元は ±1 であり、その既約元は素数である)、および「その分解が各因子の並べ替えと因子にいくつかの単元を掛ける違いを除いて一意である」—という性質を共有している。一意分解可能であるという性質を持つ整域を一意分解整域 (UFD) と呼ぶ。
- 注意
- 零でも単元でもない元を「既約元」の積に分解するような因子分解を「既約元分解」と呼び、「素元」の積に分解されるとき「素元分解」と呼ぶ。素元は必ず既約元であったから素元分解は既約元分解の一種であるが、実はその分解は一意である[注釈 3]、しかし必ずしも逆(「既約元が必ず素元となる」という性質)は言えないから素元分解でない既約元分解を持つ整域は存在する(これは一意分解可能性質のうち、分解可能よりも一意性の方が困難な性質であることを含意している)。一般に、既約元分解可能な整域は原子整域 (AD)[1]あるいは分解整域 (factorization domain[2]; FD) と呼ばれる。一方、「既約元が必ず素元となる」という性質はユークリッドの補題と呼ばれ(これは Z の既約元として定義される素数が Z の素元であることを述べたユークリッドによる補題に名称を因む)、ユークリッドの補題を満たす整域をEL整域 (ELD) と呼ぶ。明らかに、ELDかつADなる整域において既約元分解は素元分解であり、したがって一意分解である。
UFD において零でも単元でもない任意の元からなる部分集合に対して最大公約元が存在する。逆にそのような任意の部分集合に対して最大公約元を持つ整域は UFD になる。任意の PID は UFD である。
整数の環 Z と同様のユークリッド除法が定義される整域はユークリッド整域と呼ばれる。任意のユークリッド整域は PID であり、したがって UFD となる。ユークリッド整域において最大公約数の計算に利用できるユークリッドの互除法が定義できるが、それが因数分解アルゴリズムの存在を意味しないことには注意すべきである。適当な体 F 上の一変数多項式の成すユークリッド環 F[X] でその中で一般の多項式に適用可能な因数分解アルゴリズムが無いような F の具体例が存在する。
イデアルの準素分解[編集]
代数的整数論において、ディオファントス方程式の研究の過程で19世紀の数学者は整数を一般化するものとしての代数的整数を導入した。初期に知られた代数的整数環はガウス整数環やアイゼンシュタイン整数環で、これらは通常の整数の場合と同じくPID(したがってUFD)であった。しかし事はそう都合よくはいかず、すぐにほとんどの代数的整数環がPIDでもUFDでもないことが判明する。もっとも簡単な例として、ℤ[√−5] において
このように分解の一意性が成り立たないことはディオファントス方程式の解法にとって大きな困難をもたらすものであった。例えば、フェルマーの最終定理に対するかなり多く誤った証明が分解の一意性を暗に仮定したことによる誤りを犯していたのである(「真に驚くべき証明を発見したが、この余白はそれを記すには狭すぎる」と書き残したことで知られるピエール・ド・フェルマーもおそらく例外ではあるまい)。この困難を解決したのはリヒャルト・デーデキントで、それは任意の代数的整数環がイデアルの一意な準素分解を持つという形に述べられる。すなわち、これらの環において、任意のイデアルは準素イデアルの積として表され、その分解は因子の順番を除いて一意である。イデアルに関するこの一意分解性質を持つ整域は、こんにちデデキント整域と呼ばれている。デデキント整域は、それを代数的整数論の基礎たらしめる良い性質を多く持つものである。
行列の因子分解[編集]
行列環は非可換であり、行列の積は一意分解を与えない(すなわち、ひとつの行列をほかの行列の積として書く方法が一般に複数存在する)から、行列の分解は特定の種類の因子からなるものを考えなければ意味を為さない。例えば、LU分解では下三角行列 L と上三角行列 U の積 LU としての分解を考えるものである。LU分解は常に可能であるわけでなく、一般には第三の因子として置換行列 P を含めたLUP分解を考える。
論理行列は二項関係を表現するもので、行列の積が関係の合成に対応する。論理行列の分解を通して関係を分解することは、difunctional関係のような関係の特質 (nature) の輪郭 (profile) を供与するものである。
脚注[編集]
注釈[編集]
出典[編集]
- ^ arXiv探訪 2016-09-27 22.一意分解整域(個人ブログ)
- ^ PETE L. CLARK (PDF), FACTORIZATION IN INTEGRAL DOMAINS. p. 9. note. 5 も参照.
外部リンク[編集]
- Weisstein, Eric W. "Factorization". mathworld.wolfram.com (英語).
- Definition:Divisor_(Algebra)/Factorization at ProofWiki










