微分積分学における積の法則(せきのほうそく、英: product rule;ライプニッツ則)は、二つ(あるいはそれ以上)の函数の積の導函数を求めるのに用いる公式。
この公式は、

あるいはライプニッツの記法では

と書くことができる。
あるいは無限小(あるいは微分形式)の記法を用いて

と書いてもよい。
三つの函数の積の導函数は

である。
発見者について[編集]
積の法則の発見者はゴットフリート・ライプニッツであると言われる[注 1]。ライプニッツは無限小(微分)を用いてこれを示した。
その内容は、u(x), v(x) を x を変数とする二つの可微分函数とするとき、積 uv に対応する無限小は

で与えられるはずだが、項 du⋅dv は(du および dv に比べて)「無視できる」(高位の無限小)ことから、ライプニッツは

であると結論付けた。実際、これが積の法則の微分形である。
両辺を無限小 dx で割るならば

が得られ、これはまたラグランジュの記法によって

と書くこともできる。
- ƒ(x) = x2 sin(x) を微分したい場合、積の法則を用いて ƒ'(x) = 2x sin(x) + x2cos(x) が得られる(x2 の導函数は 2x で sin(x) の導函数は cos(x) であった)。
- 任意の定数は微分すると 0 になることから、積の法則の特別な場合として「定数倍の法則」:
c が
実定数で
ƒ(x) が可微分函数のとき、定数倍
cƒ(x) もやはり微分可能で、その導函数は
(cƒ)'(x) = c × ƒ′(x) で与えられる。
が得られる。これと和の微分法則を合わせれば、函数を微分することが線型変換であることがわかる。
- 部分積分の公式は積の法則から導かれる。同様に(弱い意味での)商の法則も積の公式の帰結である(ここで「弱い意味で」というのは、商の微分可能性は保証せず、商が微分可能である場合に「限って」その導函数がどのような形になるかを述べるということ)。
厳密な証明[編集]
標準的な微分積分学の場合[編集]
積の法則の厳密な証明には、微分の定義と極限の基本性質を用いる。
積 h(x) = f(x)g(x) について、各因子 f, g は一点 x0 においてそれぞれ微分可能であるものとする(以降、本節を通して x0 は固定するものとする)。主張は、積 h が点 x0 において微分可能であること、およびその微分係数 h'(x0) が f'(x0)g(x0) + f(x0)g'(x0) で与えられることの二点である。
差分 Δh := h(x0+Δx) - h(x0) を考える。x0 は固定しているといっても、Δh は Δx の値(これは十分に「小さい」ものと考える)に依存して変化することに注意せよ。
積 h が x0 において微分可能であるということは、極限

が存在するという意味であり、また微分可能であるとき h'(x0) はこの極限の値として定義されるのであった。
Δh と同様に、Δf := f(x0+Δx) - f(x0) および Δg := g(x0+Δx) - g(x0) と定める。これらはやはり Δh と同じく Δx の函数になる。このとき f(x0+Δx) = f(x0) + Δf および g(x0+Δx) = g(x0) + Δg である。
さてこのとき、h(x0+Δx) = f(x0+Δx)g(x0+Δx) = (f(x0) + Δf)(g(x0)+Δg) を分配法則に従って展開すれば、

(∗)
を得る。証明自体には不必要だが、この積を以下のような面積図
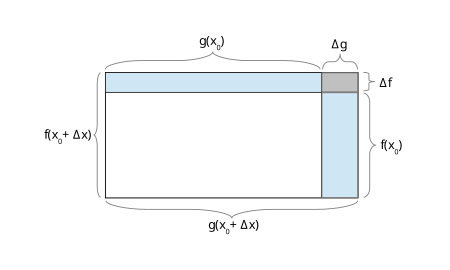
を用いて図形的に表すのも理解の一助となるであろう。Δh の値を得るには、先の等式 (∗) から h(x0) = f(x0)g(x0) を引けばよいのだから、面積図で言えば白い矩形の面積を除く残りの三矩形の面積にあたる

を得る(右辺の前二項は面積図で言うところの青い矩形の面積に相当し、三番目の項は灰色の矩形の面積に相当する)。
微分係数 h'(x0) を求めるためには

(∗∗)
の Δx を 0 に近づけた極限を求めねばならない。極限の基本性質と微分の定義を用いて、一項づつ処理していこう。まずは

であり、同様に

を得る。最後の項については、Δf⋅Δg が「二階の無限小」だから結局は無視できる(極限は 0 になる)のだけれども、これを厳密に言うならば

において、g は連続であるから Δg の極限は 0 となることを用いる。結論には変わりないが

という形で述べてもよい。こうして等式 (∗∗) の三項がそれぞれ極限を持つことが示されたから、したがって極限

は存在し、その値は三項の極限の和に等しい。即ち、積 h(x) は点 x0 において微分可能であり、その微分係数は

で与えられる。これが所期の結果であった。
定義により f, g: R → R が一点 x で微分可能ならば

と書くことができる。ここで o はランダウの記号で

を意味する。このとき、

だから、h を 0 に近づける極限をとって所期の結果を得る。
対数微分と四分平方を使った証明[編集]
f = uv に対して u と v がともに x の正値函数であるならば、

ゆえ、両辺を微分して

となるから、左辺には f, 右辺には uv を掛けると(もちろん f = uv なのだから)

を得る[3]。微分可能な u, v は連続でなければならないから、正値性に関する仮定は一般性を落とすものでないことに注意せよ。
この証明では積の法則より深い結果である連鎖律と自然対数の性質が使われており(とは言っても、対数の微分に関する情報は、c を定数として cx の任意の底に対する対数を x = 1 で微分してから c を一般化することによって知ることができるから、先の証明は証明の一形態として十分に意味を成しうる)、ある意味では分の悪い証明ということになる。一方、この証明では単純明快な代数的操作しかせずに済むので、定義から直接証明するよりも恐らく理解は容易であろう。
同様の、しかし(対数の微分ができなくても証明できるという意味で)確実にさらに容易な方法として、自乗差乗算(英語版)(四分の一平方乗算)を用いるものがある。これには、やはり連鎖律と、それから四分平方函数 q (即ち、q(x) := x2/4) の性質

が用いられる。この等式の両辺を微分すれば、

を得る。この証明だと先ほどの証明のように函数の値が正か負かというのは問題にならないし、函数 q の性質も随分容易に示される。
これらの証明は函数の値が数値あるいはそれと同様の性質を持つ対象ならば意味を成す。特に行列などは、先ほどの対数の c を変化させる方法で c に代入することに意味を持たせることができるから、これを適用できる。
連鎖律からの導出[編集]
多変数の連鎖律の特別な場合として積の法則を捉えることもできる。

超準解析による定式化[編集]
u, v は x の連続函数とし、dx, du, dv は超準解析の枠組みにおける無限小、特に超実数とする。標準部函数 st は有限超実数に対して無限に近い実数を割り当てるものとすれば、

と計算できる。(このとき標準部分を取る代わりに)同質性の超限法則(英語版)を適用することを考えれば、これは本質的にライプニッツの証明である。
滑らかな無限小解析の場合[編集]
ローヴェアの無限小(滑らかな無限小解析を参照)の意味で、dx を複零(自乗して 0 になる)無限小とする。このとき、du = u'dx および dv = v'dx で,

と計算できる。

に注意せよ。
一般化[編集]
多因子化[編集]
積の法則を二つよりも多い因子を持つ積の場合にも一般化することができる。例えば、因子が三つの場合は

である。函数列 f1, …, fk に対しては
![{\displaystyle {\frac {d}{dx}}\left[\prod _{i=1}^{k}f_{i}(x)\right]=\sum _{i=1}^{k}\left({\frac {d}{dx}}f_{i}(x)\prod _{j\neq i}f_{j}(x)\right)=\left(\prod _{i=1}^{k}f_{i}(x)\right)\left(\sum _{i=1}^{k}{\frac {f'_{i}(x)}{f_{i}(x)}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a76575fff7ef09af966a5912375859666fd2d9a1)
と書ける。
高階化[編集]
因子が二つの積の n-階導函数に対しても積の法則(ライプニッツ則)は一般化することができて、

が成り立ち、一般ライプニッツ則と呼ばれる。これは二項定理と非常に似た形をしている(二項係数の項も参照)。
高階偏導函数版[編集]
偏導函数に対する積の法則は

と書ける。ただし、添字 S は集合 {1, …, n} の 2n 個ある部分集合の全てに亙る。例えば n = 3 のときは

となる。
バナッハ空間に値を取る場合[編集]
X, Y, Z はバナハ空間(例えばユークリッド空間)とし、B: X × Y → Z は連続双線型作用素とする。このとき B は微分可能で、その一点 (x,y) ∈ X × Y における導函数は

で与えられる線型写像 D(x,y)B: X × Y → Z である。
導分作用素の定義[編集]
抽象代数学では、積の法則の方が公理として先にあって、そこから導分作用素(微分作用素)と呼ばれるものが「定義」される。
ベクトル値函数の場合[編集]
ベクトル値函数のスカラー乗法、点乗積、交叉積についても積の微分法則は拡張できる。
- スカラー乗法に対する積の法則

- 点乗積に対する積の法則

- 交叉積に対する積の法則

(注意すべきこととして、交叉積は交換的ではないから

と書いてしまったら誤りである。しかし交叉積は反交換的であるから、

と書くことはできる)。
スカラー場の場合[編集]
スカラー場の勾配の概念に対してもやはり同様の積の法則

が成立する。
諸公式の導出[編集]
積の法則の応用として最たるものが、n が正の整数であるときの冪函数に対する公式

の証明である(この式自体は n が正でなくとも、あるいはさらに整数でなくとも成立するが、その証明には別の方法を考える必要がある)。証明は冪指数 n に関する数学的帰納法を用いる。n = 0 のとき xn は定数で、nxn−1 = 0 だから式は成り立つ(定数函数の導函数は 0 であるから)。任意にとって固定した冪指数 n で帰納法の仮定が成り立つならば

となるから n + 1 でも等式は成り立つ(二つ目の等号は積の法則の適用、三つ目の等号は帰納法の仮定である)。
接空間の定義[編集]
積の法則はある抽象的な図形(可微分多様体)の抽象接空間の定義にも用いられる。この定義は考えている図形の周りにある全空間を使えない若しくは使いたくない場合に利用できる(そもそも全空間というものが存在しないことだってあり得る)。それには図形上の実数値函数の専ら一点 p のみにおいて微分係数と積の法則が定義という事実を利用する。実はこのような微分係数全体の成す集合が、接空間と見るにふさわしいベクトル空間を成すのである。
- ^ ただし、ライプニッツの論文の英訳者であるJ・M・チャイルドは、その訳書の脚注でアイザック・バローによるものだと主張している[2]。
出典 [編集]
参考文献[編集]
関連項目[編集]


































![{\displaystyle {\frac {d}{dx}}\left[\prod _{i=1}^{k}f_{i}(x)\right]=\sum _{i=1}^{k}\left({\frac {d}{dx}}f_{i}(x)\prod _{j\neq i}f_{j}(x)\right)=\left(\prod _{i=1}^{k}f_{i}(x)\right)\left(\sum _{i=1}^{k}{\frac {f'_{i}(x)}{f_{i}(x)}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a76575fff7ef09af966a5912375859666fd2d9a1)











