普遍性
数学において普遍性(英語: universality、または universal property)とは、ある特定の状況下において一意に射(あるいは準同型、構造を保つ写像)を定めるような抽象的性質で、それが特定の構成(例えば直積や直和、加群のテンソル積、距離空間の完備化など)を特徴づけるようなものをいう。
普遍性の具体例となる構成には他にも、様々な構成における自由対象、核や余核、順極限および逆極限、群に対するアーベル化、集合や様々な空間に対する引き戻しや押し出し(英語: pushout)、ストーン-チェックのコンパクト化などが存在する。
このような構成は個別の数学の分野において議論されていたが、横断的な議論を試みたのは1948年のピエール・サミュエル (en:Pierre Samuel) の論文[1]によって初めて行われ、その後ブルバキによって広められたとされる[2]。
概要[編集]
U : D → C を 圏 D から圏 C への関手とし、X をC の対象とする。X から U への普遍射 (universal morphism) は、D の対象 A とCの射 φ : X → U(A) からなる対(A, φ)で表され、かつ以下の普遍性(universal property)を満たす。
- Y がDの対象で f : X → U(Y) が C の射であるような場合、常に D の射 g : A → Y が一意に存在して、次の図を可換にする。
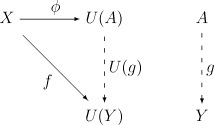
射 g の存在は、直感的には(A, φ)が「十分に一般的」であることを示しながら、一方で射の一意性は、(A, φ)が「過度に一般的ではない」事を表している。さらに、次の関係も成り立つ[3]。
また、上述の定義で全ての射を逆向きにすることで、圏論的な双対を考えることができる。U から X への普遍射は、Dの対象A とCの射 φ : U(A) → X の対(A, φ)で表され、かつ以下の普遍性を満たす。
- Y が Dの対象で f : U(Y) → X がCの射であるような場合、常に D の射g : Y → A が一意に存在して、次の図を可換にする。
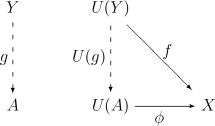
ここで、人によっては一方を普遍射と呼び、もう一方を余普遍射(co-universal property)と呼ぶ場合もある事に注意されたい。どちらがどちらかはその人次第である。
表現可能関手による定義[編集]
エミリー・リール(Emily Riehl)は『Category Theory in Context』において、圏 C の対象 c に対する普遍性(英: universal property)を次のように定義している[4]:
- 定義
- 圏 C の対象 c の普遍性は、表現可能関手 F: C → Set と、米田の補題を通して自然同型 C(c, _) ≅ F(または C(_, c) ≅ F)を定める普遍要素(英: universal element)x ∊ Fc によって表現されるものである。
(ここで Set とは集合の圏のことである。)
定義を言い換えると、c ∊ C の普遍性とは、(表現可能)関手 F: C → Set と x ∊ Fc を用いて米田の補題から定まる自然変換 C(c, _) → F が自然同型であるという性質のことである。
圏 C が小さなhom集合を持つ(各対象 x, y について C(x, y) ∊ Set である)とき、前節で定義した普遍射は普遍要素の特別な場合である。また逆に、普遍要素は普遍射の特別な場合である[5]。
例[編集]
ベクトル空間のテンソル積[編集]
体 K 上のベクトル空間 V, W について、任意の双線形写像 f: V × W → X に対して f = f'◦g を満たす準同型 f': T → X がただ1つ存在するような K-ベクトル空間 T と双線形写像 g: V × W → T の組が、同型を除いてただ1つ存在する。このときの T を V ⊗ W と表し、V と W のテンソル積と呼ぶ。
テンソル積を特徴づけるこの性質もまた普遍性と呼ばれる。実際、テンソル積の普遍性から、圏論的な普遍性が次のように与えられる:いま、V × W からの双線形写像の集合を与える対応は関手 Bilin(V, W; _): VectK → Set (VectK とは K-ベクトル空間とその間の線形写像からなる圏)を定める。このとき、テンソル積の普遍性から自然同型 VectK(V ⊗ W, _) ≅ Bilin(V, W; _) が定まり、従って Bilin(V, W; _) は表現可能関手である。双線形写像 g: V × W → V ⊗ W はこのとき、同型 VectK(V ⊗ W, V ⊗ W) ≅ Bilin(V, W; V ⊗ W) によって恒等射が写る先として定まる[6]。
また、カノニカルな双線形写像 g: V × W → V ⊗ W は一点集合からの写像 ψ:*→ Bilin(V, W; V ⊗ W) によっても表される。いま、任意の X ∊ VectK とh:*→ Bilin(V, W; X) に対して、テンソル積の性質から h = h'◦ψ が成り立つような準同型 h': V ⊗ W → X がただ1つ定まる。従って h は一点集合から Bilin(V, W; _) への普遍射である。
剰余群への射影[編集]
群 G の正規部分群 K について、剰余群 G/K への射影を φ: G → G/K で表す。群準同型 f: G → H について、K が f の核 Ker f (f(x) が H の単位元となる G の元の集合) に含まれるとき、群の準同型定理によって f = h◦φ を満たす群準同型 h: G/K → H がただ1つ存在することがわかる。
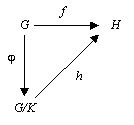
(小さな) 群とその間の群準同型からなる群の圏を Grp で表す。群 H に対して、群準同型 f: G → H であって Ker f ⊂ K を満たすものの集合を FH とおくと、この対応は関手 F: Grp → Set をなす。準同型定理の主張から、任意の H に対して同型 FH ≅ Grp(G/K, H) が存在して、さらに唯一性からこの同型は H について自然であることがわかる。
以上のことから、剰余群 G/K と剰余群への射影 φ: G → G/K は普遍性を持っていることがわかる。普遍性の帰結として、商群についての他のすべての性質は、これ以上余集合(剰余群の通常の構成で使われる G/K の各要素)に言及しなくてよくなる[7]。
ファン・カンペンの定理[編集]
位相空間 は、2つの開部分集合 によって覆われるものとする。すなわち、 が成り立つとする。このとき、共通部分 からの包含写像 と による可換図式は、位相空間の圏 Top において普遍性を持つ。すなわち、連続写像 f: U → Y と g: V → Y が f ◦ i = g ◦ j を満たすとき、f = h ◦ j' と g = h ◦ j' を満たすような連続写像 h: X → Y がただ1つ存在する。
よい条件( は空でなく弧状連結)の下で、この図式から誘導される基本群のなす図式は同様に普遍性を持つ[8]。これを (基本群に関する)ファン・カンペンの定理と呼ぶ。

さまざまな普遍性[編集]
随伴関手との関係[編集]
(A1, φ1) を X1 から U への普遍射、 (A2, φ2) を X2 から U への普遍射とする。普遍性から、任意の射 h : X1 → X2 に対して一意な射 g : A1 → A2 が存在して、次の図式を可換にする。
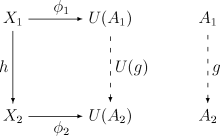
もし 全ての C の対象 Xi にU への普遍射が認められるならば、Xi Ai 及び h g によってC から D への関手 Vが定義される。 これに伴って、φi は 1C (C の恒等関手) から U V への自然変換を定義する。関手 (V, U) は随伴関手の対となる。(V は U の左随伴、及び U は V の右随伴)
同様の言明は U からの普遍射という双対な状況においても適用できる。全ての C における X について、関手 V : C → D が得られ、これは U への右随伴になっている。(つまり U は V の左随伴である。)
実際、このような方法で全ての随伴関手の対を普遍的構成から得られる。F と G を単位(unit)η と余単位(co-unit)ε (定義は随伴関手の記事を参考のこと)によって構成される随伴関手の対とする。このとき、任意の対象 C と D への普遍射が得られる。
- C の各対象 X に対し、 (F(X), ηX) は X から G への普遍射である。つまり、任意の f : X → G(Y) に対して一意な g : F(X) → Y が存在して以下の図式を可換にする。
- D の各対象 Y に対し、 (G(Y), εY) は F から Y への普遍射である。つまり、任意の g : F(X) → Y に対して一意な f : X → G(Y) が存在して以下の図式を可換にする。

普遍的構成は随伴関手の対より更に一般的である。普遍的構成は最適化問題のようなもので、この問題が C 中の全ての対象 (同様に、D の全ての対象)について解を持つとき、かつそのときのみ随伴関手の対が得られる。
脚注[編集]
- ^ Samuel, P. (1948). “On universal mappings and free topological groups” (英語). Bulletin of the American Mathematical Society 54 (6): 591–598. doi:10.1090/S0002-9904-1948-09052-8. ISSN 0002-9904.
- ^ Mac Lane 1998, p. 78
- ^ MacLane(1998) p.59
- ^ Riehl 2004, p. 62, Definition 2.3.3.
- ^ Mac Lane 1998, pp. 76–77. ただし『圏論の基礎』では「普遍要素」の定義はリールのものと異なっており、リールが「普遍要素」と呼んだものは (集合値)関手の表現(representation of a functor)として定義されているものと同値の概念である。
- ^ Riehl 2016, Example 2.3.7.
- ^ Mac Lane (1998, p. 57). 原文:
once the cosets are used to prove this one “universal” property of p : G → G/N, all other properties of quotient groups — for example, the isomorphism theorems — can be proved with no further mention of cosets (see Mac Lane-Birkhoff [1967]).
- ^ Leinster 2014, pp. 6–7, Example 0.9.
参考文献[編集]
- Paul M. Cohen (1981). Universal Algebra. D.Reidel Publishing, Holland. ISBN 90-277-1213-1
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 (2nd ed.). Springer. ISBN 0-387-98403-8
- Lainster, Tom (2014) (英語). Basic Category Theory. Cambridge Studies in Advanced Mathematics. Cambridge University Press. arXiv:1612.09375. doi:10.1017/CBO9781107360068. ISBN 9781107044241
- Riehl, Emily (2016). Category Theory in Context. Aurora: Modern Math Originals. Dover Publications. ASIN B06XHZ82GF. ISBN 9780486809038








