積 (圏論)
圏論において、考えている圏の二つの(あるいはそれ以上の)対象の(圏論的)積(せき、英: product)または直積 (direct product) は集合の直積(デカルト積)、群の直積、環の直積、位相空間の直積といった数学の他の分野における構成の背後にある本質を捉えるために考えられた概念である。本質的に対象の族の積は与えられた対象のそれぞれへの射をもつ「最も一般な」対象である。
定義[編集]
C を適当な対象 X1, X2 をもった圏とする。X1 と X2 との積とは、X1 × X2 と書かれる C の対象と二つの射 π1:X1 × X2 → X1 および π2: X1 × X2 → X2 との組で、以下の普遍性を満たすものを言う。
- 積の普遍性 (二対象の場合)
- 任意の対象 Y および射の対 f1: Y → X1 および f2: Y → X2 が与えられたとき、一意的な射 f: Y → X1 × X2 が存在して、図式

積の普遍性を表す可換図式
一意的な射 f は f1 と f2 との射の積と言い、⟨f1, f2⟩ とも書かれる。射 π1, π2 は自然な射影、標準射影 (canonical projection) あるいは射影射 (projection morphism) と呼ばれる。
いま定義したものは、二項の積であるが、より一般に集合 I で添字付けられた対象の任意の族をとり、それらの積を考えることができる。すなわち、
圏 C の対象の族 {Xi}i∈I の(C における)積とは、C の対象 X と射の族 πi: X → Xi (i ∈ I) との組で以下の普遍性を満足するものを言う。
この積 X をしばしば ∏
i∈I Xi で表す。I = {1, …, n} の場合は特に X1 × ⋯ × Xn のように書き、射の積も ⟨f1, …, fn⟩ のように書く。
等式的な定義[編集]
図式を用いる代わりに、対象の積を等式的に定めることができる。その場合例えば、二項の積は
- 一意な射 f が存在することは、二項演算 ⟨–, –⟩ の存在性によって保障される。
- 図式の可換性は等式 πi ∘ ⟨f1, f2⟩ = fi (i = 1, 2) が任意の f1, f2 について成り立つことによって保障される。
- f の一意性は任意の f に対し等式 ⟨π1 ∘ π2⟩ = f が成り立つことによって保証される[1]。
極限として[編集]
積は極限の特別な場合である。これを見るには、極限の定義で必要となる図式において離散圏(恒等射以外の射をもたない対象からなる族)を用いればよい(各離散対象は成分と射影の添字を与え、図式を関手とみれば(離散圏とみた)添字集合 I からの関手である)。このとき実際に積の定義が極限の定義と一致することがみてとれる。{fi}i∈I が錐、射影が極限(極限錐)である。
普遍構成[編集]
極限が普遍構成の特別な場合であるのと全く同じように、積もそうである。極限の普遍性を適用するのに必要なものとして、J をただ二つの対象をもつ離散圏とする(このとき CJ は単に積圏 C × C である)。対角関手 Δ: C → C × C は各対象 X に順序対 (X, X) を対応させ、各射 f に順序対 (f, f) を対応させるものである。C における積 X1 × X2 は、対角函手 Δ から C × C の対象 (X1, X2) への普遍射によって与えられる。この普遍射は C の対象 X と射 (X, X) → (X1, X2) からなり、これは射影を含んでいる。
例[編集]
集合の圏における(圏論的な意味での)積はデカルト積(集合の直積)である。与えられた集合の族 Xi (i ∈ I) に対する積は、集合 ∏
i∈I Xi ≔ {(xi)i∈I | xi ∈ Xi (∀i ∈ I)} と自然な射影の族 πi: ∏
i∈I Xi → Xj (j ∈ I) との組として定まる。ここで各射影は πj((xi)i∈I) ≔ xj を満たす写像である。
任意の集合 Y と写像の族 fi: Y → Xi が与えられたとき、普遍射 f: Y → ∏
i∈I Xi は f(y) ≔ (fi(y))i∈I として定まる。
他の例:
- 位相空間の圏における積は、各因子の台集合のデカルト積を台として積位相を入れた空間である。積位相はすべての射影が連続であるような最も粗い位相である。
- 一つの環 R 上の加群の圏における積は、台集合のデカルト積に成分ごとの加法と分配的な積を入れたものである。
- 群の圏における積は、台集合のデカルト積に成分ごとの積を入れた群の直積によって与えられる。
- 関係の圏 Rel において、積は非交和によって与えられる。(集合の圏 Set が Rel の部分圏であることを考えるとこれは少し驚かれるかもしれない。)
- 代数多様体の圏において、圏論的な積はSegre埋め込みによって与えられる。
- 半アーベルモノイド (semi-abelian monoid) の圏において、圏論的な積は history monoid によって与えられる。
- 半順序集合は順序関係を射として用いることで圏として扱うことができる。この場合積と余積は最大下界と最小上界(交わりと結び)に対応する。
議論[編集]
任意の圏において、必ずしも積が存在するとは限らない。例えば、空積(すなわち添字集合 I が空集合)は終対象と同じであり、無限群の圏のようないくつかの圏は終対象を持たない: 任意の無限群 G に対し、射 Z → G は無限個存在するので、G が終対象となることはありえない。
添字集合 I に対し、I で添字付けられる任意の族が圏 C において積を持つならば、積をとる演算を取り纏めて関手 CI → C として扱うことができる[2]。この関手が対象をどのように写すかは明らかだが、射の対応は微妙である(定義節で与えられた「射の積」とは少々異なる)。二項の積(積函手は双関手)の場合を考えると、必要となるのは f1: X1 → Y1, f2: X2 → Y2 に対して適当な X1 × X2 → Y1 × Y2 なる射を作ることで、それには積 ⟨f1 ∘ π1, f2 ∘ π2⟩ を取ればよい。射に対するこの演算を射の直積あるいはデカルト積 (cartesian product of morphisms) と呼ぶ[3]。一般の場合の積関手も同様に、族 {Xi}i∈I, {Yi}i∈I の間の射の族 fi: Xi → Yi (i ∈ I) に対して ∏
i∈I Xi → ∏
i∈I Yi なる射として、射の族 {fi ∘ πi} の積 ⟨fi ∘ πi : i ∈ I⟩ が対応する。
対象のすべての有限集合が積をもつような圏はデカルト圏 (cartesian category) と呼ばれることもある[3]。(ただし、「すべての有限極限をもつ圏」の意味でこの語を用いる文献もある。)
積は結合的である。デカルト圏 C において、上で述べたように積函手を考え、C の終対象を 1 と書けば、自然同型
が成立する。これらの性質は(同型を等式で置き換えれば)可換モノイドの性質と形の上では同じである。すなわち、有限積を備えた圏は、対称モノイド圏を構成する。
分配性[編集]
有限積および有限余積をもつ圏において、自然な射 X × Y + X × Z → X ×(Y + Z) が存在する、ただしここでプラス記号は余積を表す。これを見るために、次の図式
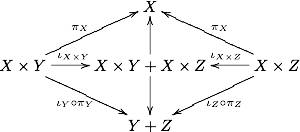
を埋める種々の射影および入射について注意を払わねばならない。
これにより X ×(Y + Z) に対する普遍性は一意な射 X × Y + X × Z → X ×(Y + Z) を保証する。分配圏は、この射が実際に同型射となるような圏を言う。従って分配圏において自然な同型
が成立する。
関連項目[編集]
参考文献[編集]
- ^ Lambek J., Scott P. J. (1988). Introduction to Higher-Order Categorical Logic. Cambridge University Press. p. 304
- ^ Mac Lane 1988, p. 37.
- ^ a b Michael Barr, Charles Wells (1999). Category Theory - Lecture Notes for ESSLLI. p. 62
- Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstract and Concrete Categories. John Wiley & Sons. ISBN 0-471-60922-6
- Barr, Michael; Charles Wells (1999). Category Theory for Computing Science. Les Publications CRM Montreal (publication PM023) Chapter 5.
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 (2nd ed.). Springer. ISBN 0-387-98403-8
- Definition 2.1.1 in Borceux, Francis (1994). Handbook of categorical algebra. Encyclopedia of mathematics and its applications 50-51, 53 [i.e. 52]. Volume 1. Cambridge University Press. p. 39. ISBN 0-521-44178-1
外部リンク[編集]
- Interactive Web page which generates examples of products in the category of finite sets. Written by Jocelyn Paine.
- Product in nLab




