群論
| 代数的構造 → 群論 群論 |
|---|
 |
群論(ぐんろん、英語: group theory)とは、群を研究する学問。 群の概念は抽象代数学における中心的な概念。
環・体・ベクトル空間などは、演算や公理が付与された群と看做すことができる。
群論の方法は代数学の大部分に強い影響を与えている。
線形代数群とリー群の理論は群論の一分野。 特に発展を遂げており、独自の適用範囲を持っている。
結晶や、水素原子などの構造の多くは、点群で表現できる。このように、群論は、物理学や化学の中に多くの実例・応用例がある。
1960年代~80年代に発表された総計1万ページを超える論文によって、完全な有限単純群の分類が達成された。これは多くの数学者の共同作業の賜物であり、20世紀後半の数学において最も重要な業績の一つである。
研究史[編集]
群論は、歴史的に3つの源泉がある。数論、代数方程式論、幾何学である。数論の系統は、オイラーに始まり、ガウスの合同式の理論、および二次体に関係した加法群・乗法群の研究によって発展した。
置換群に関する初期の研究成果は、ラグランジュ、ルフィニ、アーベルらの、代数方程式の一般解の研究の過程で得られた。
エヴァリスト・ガロアは「群」という用語を作った。 彼は、初期の群論と現在の体論を結びつけた。
幾何学については、群はまず射影幾何学で、のちに非ユークリッド幾何学で重要になった。 フェリックス・クラインはエルランゲン・プログラムにおいて、 群論は幾何学の原理を統合するものになることを予言した。
1830年代、エヴァリスト・ガロアが初めて、代数方程式の可解性の判定に、群を導入した。 アーサー・ケイリーとコーシーはこの研究を発展させ、 置換群の理論を創設した。
歴史的な2番目の源泉としては、幾何学方面からの流れがある。 可能な幾何学(ユークリッド幾何学、双曲幾何学、射影幾何学)へ群を適用したのは、 フェリックス・クラインのエルランゲン・プログラムに始まる。
1884年、ソフス・リーは群(現在リー群として知られている)を解析的問題に適用した。 三番目に、群は(最初は暗黙的に、後に明示的に)代数的整数論に用いられた。
これら初期の源流では、観点が違っていたので、そのため群に対する観念も違ったものとなっていた。 1880年頃から群の理論の統合がなされてくる。 そして、群論の影響はますます増大し、20世紀初期には抽象代数学、表現論など多くの派生分野が成立した。 有限単純群の分類は、20世紀中頃より膨大な量の研究がなされ、ついに完成に至った。
群の主なクラス[編集]
群の範囲は、有限置換群や行列群の特殊な例から、生成系と基本関係で表示される抽象群まで、いくつかのクラスに分かれていると考えることができる。
置換群[編集]
初めて系統的な研究のなされた群のクラスは置換群である。 任意の集合 X と、X からそれ自身への全単射(置換とも呼ばれる)の集まり G で合成と反転に関して閉じているようなものが与えられたとき、G は X に作用する群であるという。
X がn 個の元からなり、G が置換全体からなるならば、G は n-次対称群 Sn と呼ばれる。 一般の置換群 G は X の対称群のある部分群となっているものをいう。 ケイリーによる初期の構成では、 任意の群は(左正則表現の意味で)X = G として自分自身に作用する置換群として提示された。
多くの場合、置換群の構造は対応する集合への作用の性質を用いて調べられる。 例えば、n ≥ 5 に対する交代群 An が単純群である。 つまり、真の正規部分群を持たない。 次の方法で示すことができる。An が単純であるという事実は、高次一般代数方程式の根の冪根による表示の不可能性において重要な役割を果たす。
行列群[編集]
次に重要な群のクラスは行列群あるいは線型代数群と呼ばれるものである。ここでは群 G は体 K 上の与えられたサイズの正則行列からなる集合で、積と逆をとる操作について閉じているようなものである。そのような群は n-次元ベクトル空間 Kn に線型変換として作用する。この作用により、行列群は概念的には置換群とよく似たものとなり、また作用の幾何学は群 G の性質を示すのに最大限有効に利用することができる。
変換群[編集]
置換群や行列群は、群が空間 X にその内在的な構造を保つように作用するという、変換群の概念の特別の場合である(置換群の場合は X は集合で、行列群の場合は X はベクトル空間であった)。変換群の概念は対称変換群(あるいは「対称性の群」)の概念に近い関係にある。変換群というとある構造を保つ変換「全体」の成す群を意味することが多い。
変換群の理論は群論と微分幾何学とを結びつける橋渡しの役割を果たすものである。多様体上の同相あるいは微分同相としての群作用の考察は、リーおよびクラインに始まり、膨大な研究がなされている。ここで扱う群それ自体は、離散群かもしれないし連続群となるかもしれない。
抽象群[編集]
群論の発展の初期段階では、群としては、数、置換、行列などによって実現される「具体的」なものばかりが考察の対象であった。特定の公理系を満たす演算を備えた集合としての「抽象群」の概念が根付き始めるのは、19世紀後半になってからのことである。抽象群を特定する典型的な方法のひとつは、生成元と基本関係による表示
を通して与えられる。抽象群を与えるための最も重要な方法は、群 G とその正規部分群 H による商群あるいは剰余群と呼ばれる群 G/H を構成する操作である。代数体上のイデアル類群は早くから扱われてきた剰余群の例であり、数論において非常に重要である。群 G が集合 X 上の置換群であるとき、その剰余群 G/H はもはや X に作用しないものだが、抽象群を考えることによってこのような問題を心配する必要も無くなる。
具体的な群から抽象群へ視点を移すことにより、その群がどのように実現されているかということとは無関係に(現代的な言葉で言えば、同型のもとで不変な)群の性質について考察することが自然なものとなった。またこのような性質による群の分類も、有限群、捩れ群、単純群、可解群などといったものが考えられる。また、個々の群の性質を探ることよりも、群のクラスに対して広く適用できるような結果を確立する方法が求められた。このような新しいパラダイムは、数学の発展に対して傑出した重要性を持つものであり、ダフィット・ヒルベルト、エミール・アルティン、エミー・ネーターおよび彼らに師事した数学者たちによって、抽象代数学が構築されていく前兆となるものであった。
位相群と代数群[編集]
群に新たな構造を付け加えることにより、群の概念が発展することになった。新たな構造とは、特に、位相空間、可微分多様体、代数多様体などである。群演算(乗法 m と反転 i)
が、上記の構造と両立可能であるとき、つまりこれらが連続、滑らか、(代数幾何学的な意味で)正則な写像となっているとすると、群 G はそれぞれ位相群、リー群、代数群と呼ばれるものになる[注 1]。 群に別種の構造を付け加えることによって、これらの種類の群と、数学の別の分野が関連づけられる。そして、違う手法を研究に適用することが可能になる。
組合せ論的群論と幾何学的群論[編集]
群を記述するのには複数の方法がある。有限群は、可能な全ての積 g * h によって構成される乗積表を書き出すことによって記述することができる。もう一つの主要な方法としては、「生成系(生成元)と関係式」によって群を定義する方法であり、これは群の表示と言われる。
群 G の生成系を与える任意の集合 F = {gi}i ∈ I が与えられたとき、F の生成する自由群から群 G への全射準同型が存在する。この全射準同型の核は F のある部分集合 D で生成され、基本関係のなす部分群と呼ばれる。このような群の表示は、ふつう ⟨F | D⟩ と書かれる。例えば、整数全体の成す加法群 Z = ⟨a | ⟩ はただ一つの元 a (= ±1) によって生成され、基本関係を持たない(n が 0 でない限り n1 は 0 ではないから)群である。生成元に対応する記号からなる文字列は語 (word) と呼ばれる。
組合せ論的群論は、群を生成元と基本関係の側面から研究する学問である[1]。これは、特に何らかの有限性条件、例えば有限生成であるとか有限表示を持つ(つまり、有限生成かつ基本関係が有限個しかない)というような条件が仮定されている場合に有用である。この分野は、その基本群を通してグラフ理論との関係を利用することができて、例えば自由群の任意の部分群が自由であることが示せる。
群を生成元と基本関係によって与える方法から、いくつかの問題が自然に生じてくる。語の問題というのは「群の生成元からなる二つの語が、いつその群の同じ元を定めるか」というものである。この問題をチューリングマシンに関連付けることにより、この問題を一般に解決することのできるアルゴリズムが存在しないことを示すことができる。同じくらい困難な問題に「異なる表示によって与えられる二つの群が、いつ互いに同型となるか」という同型問題がある。例えば、さきほどの加法群 Z は
- ⟨x, y | xyxyx = 1⟩
とも表すことができるが、この表示と先ほどの表示とが同型な群を与えるということは、表示だけ見れば自明なことではない。
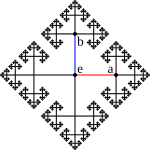
幾何学的群論とは、語の問題や同型問題といった問題に対して、群を幾何学的対象として見たり、群が作用する適当な幾何学的対象を求めるといったような幾何学的な視点から解決を試みるものである[2]。前者の方法としては、群の元を頂点とし、右からの乗法によって写りあう元を辺で結んだケイリーグラフがある。二つの元が与えられれば、それらの元を結ぶ最短経路の長さとして語の距離が定義できる。後者のやり方として、ミルナーと Svarc による、(コンパクト多様体のような)距離空間 X に適当な方法で作用する群 G が与えられれば、群 G は空間 X に擬等長 (quasi-isometric) であるという定理がある。
群の表現[編集]
群 G が集合 X に作用するとは、G の各元が、X 上定義された全単射で群構造と両立するものを定めることをいう。ただし、X にさらに構造が入っているときは、それに応じて表現の概念に制限を加えるほうが有効である。例えばよくある状況として、群 G のベクトル空間 V における(または V を表現空間とする)表現(線型表現)とは、GL(V) を V 上の正則線型変換全体の成す群として、群準同型
- ρ: G → GL(V)
のことをいう。これはつまり、群 G の各元 g に線型自己同型 ρ(g) が割り当てられていて、さらに G の別の任意の元 h に対して ρ(g) ∘ ρ(h) = ρ(gh)が成り立つということである。
この定義は二つの方向性で捉えることができて、いずれの仕方でも(群コホモロジーや同変 K-理論のような)数学のまったく新たな領域を生じる。ひとつは、群 G について新たな情報をもたらすものである。例えば群 G における演算はしばしば抽象的に与えられるけれども、表現 ρ を通じて(特に表現が忠実のとき)群演算は行列の積という非常に具体的なものに対応付けられることになる。もうひとつは、よく知られた群が与えられ、それが複雑な対象に作用しているものとすれば、そのような対象を調べるのが簡単になるというものである。例えば、G が有限群とすれば、表現空間 V が既約表現の直和に分解されるというマシュケの定理が知られているが、既約表現に対してはシューアの補題などが利用できるので、V 全体を考えるよりもずっと扱いやすい。
与えられた群 G に対する表現論とは、G の表現としてどのようなものが存在しうるかを問うものである。状況設定はさまざまで、どのような手法を使えるかとか、どのような結果が得られるかというようなことがそれぞれの場合で変わってくる。有限群の表現論およびリー群の表現論は表現論における二大主要テーマである。群の表現の全体像は群の指標によって統制されている。例えば、フーリエ多項式は、周期函数全体の成す L2-空間に作用する、絶対値 1 の複素数全体の成す群 U(1) の指標として解釈することができる。
群と対称変換[編集]
与えられた任意の種類の構造を持つ対象 X に対し、その対称変換(あるいは対称性、symmetry)とは対象 X からそれ自身の上への構造を保つ変換のことを言う。これは多くの場面で見つかるが、たとえば
- 対象 X が特に付加的な構造を持たないただの集合であるとき、X の対称変換とは集合 X からそれ自身への全単射のことであり、その全体として対称群が得られる。
- 対象 X が距離構造を備えた平面上の点の集合(あるいはもっとほかの距離空間)であるとき、X の対称性とは集合 X 上の全単射であって、X 上の任意の二点間の距離を保つもの(等距変換)のことである。これに対応する群は X の等距変換群と呼ばれる。
- 先ほどと同じ集合で距離の代わりに角を保つものは共形写像あるいは等角写像と呼ばれる。等角写像の全体からは、例えばクライン群が得られる。
- 対称変換は何も幾何学的対象に限ったものではなく、代数的対象にも同様に定義することができる。例えば、方程式は二つの根 ±√3 を持つが、このとき、この二つの根を入れ替えるという対称変換が考えられ、これによって得られる群が、この方程式に属するガロア群と呼ばれるものである。一変数の任意の代数方程式が、その根の上のある種の置換群としてのガロア群を持つ。
群の公理は対称変換の本質的な性質を定式化するものであり、対称変換の全体は群を成す。実際、対象に対称変換を施してからさらに別の対称変換を施せば、得られる結果は再び対称変換であるから、対称変換は写像の合成に関して閉じている。また、対称を固定して動かさない恒等変換はかならずそ対象の対称変換である。逆元の存在については、対称変換の取り消しができるということによって保証され、群演算の結合性は対称変換が空間上の写像であり、写像の合成が結合的であることから従う。
フルフトの定理 (Frucht's theorem) は「任意の群は、あるグラフの対称変換群である」ことを主張するものである。従って任意の抽象群は、実際にある具体的な対象の上の対称変換の成す群として得られることになる。
対象の「構造を保存する」という言及は、圏で考えればもっと厳密に扱うことができる。つまり、構造を保つ写像とは射のことであり、対称変換群(対称性の群)とは考えている対象の自己射群である。
群論の応用分野[編集]
群論の応用は広く、抽象代数学における殆ど全ての構造は群の特殊なものと見ることができる。例えば環はアーベル群(加法に対応)に第二の演算(乗法に対応)を合わせて考えたものと見ることができる。したがって、それらの代数的構造の理論の多くの部分が群論的な議論を下敷きとして行うことができる。
ガロア理論は群を多項式の根の対称性(もっとちゃんと言えば、根が生成する多元環の自己同型)を記述するのに用いる。ガロアの基本定理は体の代数拡大と群論との関係性を与えるものである。これにより、代数方程式の可解性の効果的な判定法が、対応するガロア群の可解性によって与えられる。例えば、5-次の対称群 S5 が可解でないということから、五次の一般方程式が(低次の方程式で可能であったようには)冪根を用いて解くことができないという事実が従う。ガロア群は歴史的には群論の起源の一つではあるが、未だ類体論などの領域で新しい結果を与えるなどの実りある応用がされている。
代数的位相幾何学(代数トポロジー)は、その研究の対象となるものにはっきりと群が付随しているもう一つの領域である。ここでは、群は位相空間のある種の不変量を記述するのに用いられる。「不変量」というのは、空間がある種の変形を受けてもそれらが変化しないということを示すものである。例えば、基本群は、空間に本質的に異なる道がいくつあるかを「数える」ものである。(2002年と2003年にグレゴリー・ペレルマンによって証明がなされた)ポワンカレ予想はこのような考え方を用いた顕著な応用例であるが、その影響はこの方面に留まるものではない。たとえば、代数的位相幾何学では所定のホモトピー群を備えた空間であるアイレンバーグ-マクレーン空間が用いられる。同様に代数的 K-理論は群の分類空間についての重要な手法を与える。あるいは、(無限群の)捩れ部分群という名称は、群論における古い形の位相幾何学の影響を示すものである。

代数幾何学と暗号理論は、同じように群論を至る所で取り入れている。アーベル多様体は、群作用の存在によって、詳細な調査が可能になる。一次元の場合では、楕円曲線が詳細に研究されている。これらは理論的にも応用的にも興味深いものである[注 2]。楕円曲線暗号では、非常に大きな素数位数の群が構成され、公開鍵暗号として役に立っている。
代数的整数論は、群論の特殊な場合である。例として、オイラー積の公式
は「任意の整数は素数の積にただ一通りに分解される」という算術の基本定理に基づく。これがもっと一般の環では必ずしも成立しないことで、イデアル類群や正則素数の概念が生じた。クンマーがフェルマーの最終定理を扱う際に用いている。
- リー群(数学者ソフス・リーの名前にちなむ)は、微分方程式と多様体の研究において重要である。これは、連続幾何的構造および解析的構造の対称性を記述するものである。リー群などの群の解析を調和解析という。ハール測度(リー群の平行移動不変積分)は、これはパターン認識や画像処理に使われている[3]。
- 組合せ数学においては、置換群や群作用の概念がしばしば使われ、集合の個数を計測する助けになる。バーンサイドの補題も参照。
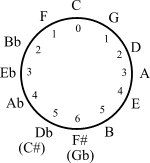
- 五度圏には12周期群(巡回群)が現れる。
- 物理学においては、群は物理の法則に現れる対称性を記述するために使われる。物理学者は、群の表現、特にリー群の表現に興味を持っている。なぜならそれはしばしば、「可能な」物理法則を指し示すからである。物理における群論の応用には、たとえば標準模型、ゲージ理論、ローレンツ群、ポアンカレ群などがある。
- 化学、材料科学においては、群はおもに結晶構造や分子対称性を分類するのに使われる。構造に対応した点群により、物理的な性質(極性やキラリティ)や分子軌道を決定できる。ラマン分光法や赤外分光法も参照。分子の対称性は、化合物の多くの物理的・分光学的特性に関与しており、分子の対称性により化学反応がどのように起こるかを予想できる。与えられた分子に点群を割り当てるためには、その分子に存在する対称操作の集合を見つける必要がある。対称操作と対称要素は不可分の概念である。物体の位置と配向を、移動が行われる前と後で注目したとき、これら二つの場合の位置と配向が区別できないようならば、その移動が対称操作である。一方で、対称要素とは、幾何学的な意味での、線、面、点などであり、それらに関して一つまたはそれ以上の対称操作が行われるものである。以下で対称操作について詳しく説明する。化学では、以下の5つの重要な対称操作がある。それらは、同一性操作(E)、回転操作または本義回転(proper rotation)(Cn)、反射操作または鏡映(σ)、反転操作(i)、および回転反射操作または転義回転(improper rotation)(Sn)である。同一化操作(E)は、分子をそのままにしておくことからなる。これは、任意の軸を中心とした任意の数の全回転に相当する。つまり同一性操作は、すべての分子がもつ対称操作である。軸周りの回転(Cn)は、分子を特定の回転軸を中心とした角度360°/n(nは整数)を通る回転である。例えば、水分子(H₂O)において、酸素原子と二つの水素原子を含む平面上で二つのO-H結合のなす角を二等分する軸を中心に180度回転した場合は、開始時と同じ構成になる。この場合、n = 2となるので、水分子はC₂の対称要素をもつ。複数の回転軸を有する分子において、nの値が最も大きいCn軸が最高位の回転軸または主軸である。例えばボラン(BH3)の場合、回転軸の最高次数はC₃なので、回転軸の主軸はC₃となる。鏡映(σ)は、分子内に位置する対称面に対し分子を反転する操作である。対称面が回転主軸に対して垂直な場合をσh(水平)といい、回転の主軸を含む他の平面は、σvまたはσdである。例えば、水分子(H₂O)において、対称面は主軸を含むものしかないので、2つの対称要素σvを持つことになる。反転操作(i)は反転中心に対し分子を対称移動する操作である。水分子においては、反転中心が存在しない。回転反射操作または転義回転(improper rotation)(Sn)は回転してから、ついで回転軸に垂直な面内での鏡映という順序の操作を一つあるいはそれ以上繰り返す操作である。水分子においては転義軸を持たない。以上より、水分子は、E,C₂,二つのσvを対称要素として持つことが分かる。これから水分子はC₂vの点群に属することが分かる。
脚注[編集]
注釈[編集]
- ^ このように新しい構造を付加する手順は、適切な圏における群対象 (group object) の概念として定式化される。リー群は可微分多様体の圏における群対象であり、アフィン代数群はアフィン代数多様体の圏における群対象である。
- ^ ミレニアム問題の一つであるバーチ・スウィンナートン=ダイアー予想を見よ。
出典[編集]
- ^ Schupp & Lyndon 2001
- ^ La Harpe 2000.
- ^ Lenz, Reiner (1990), Group theoretical methods in image processing, Lecture Notes in Computer Science, 413, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-52290-5, ISBN 978-0-387-52290-6.
参考文献[編集]
洋書[編集]
- Borel, Armand (1991), Linear algebraic groups, Graduate Texts in Mathematics, 126 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-97370-8, MR1102012
- Carter, Nathan C. (2009), Visual group theory, Classroom Resource Materials Series, en:Mathematical Association of America, ISBN 978-0-88385-757-1, MR2504193
- Cannon, John J. (1969), “Computers in group theory: A survey”, Communications of the Association for Computing Machinery 12: 3–12, doi:10.1145/362835.362837, MR0290613
- Frucht, R. (1939), “Herstellung von Graphen mit vorgegebener abstrakter Gruppe”, Compositio Mathematica 6: 239–50, ISSN 0010-437X
- Golubitsky, Martin; Stewart, Ian (2006), “Nonlinear dynamics of networks: the groupoid formalism”, Bull. Amer. Math. Soc. (N.S.) 43: 305--364, doi:10.1090/S0273-0979-06-01108-6, MR2223010 Shows the advantage of generalising from group to en:groupoid.
- Judson, Thomas W. (1997), Abstract Algebra: Theory and Applications An introductory undergraduate text in the spirit of texts by Gallian or Herstein, covering groups, rings, integral domains, fields and Galois theory. Free downloadable PDF with open-source GFDL license.
- Kleiner, Israel (1986), “The evolution of group theory: a brief survey”, en:Mathematics Magazine 59 (4): 195–215, ISSN 0025-570X, MR863090
- La Harpe, Pierre de (2000), Topics in geometric group theory, University of Chicago Press, ISBN 978-0-226-31721-2
- Livio, M. (2005), The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry, Simon & Schuster, ISBN 0-7432-5820-7 Conveys the practical value of group theory by explaining how it points to symmetries in physics and other sciences.
- Mumford, David (1970), Abelian varieties, Oxford University Press, ISBN 978-0-19-560528-0, OCLC 138290
- Ronan M., 2006. Symmetry and the Monster. Oxford University Press. ISBN 0-19-280722-6. For lay readers. Describes the quest to find the basic building blocks for finite groups.
- Rotman, Joseph (1994), An introduction to the theory of groups, New York: Springer-Verlag, ISBN 0-387-94285-8 A standard contemporary reference.
- Schupp, Paul E.; Lyndon, Roger C. (2001), Combinatorial group theory, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41158-1
- Scott, W. R. (1987) [1964], Group Theory, New York: Dover, ISBN 0-486-65377-3 Inexpensive and fairly readable, but somewhat dated in emphasis, style, and notation.
- Shatz, Stephen S. (1972), Profinite groups, arithmetic, and geometry, Princeton University Press, ISBN 978-0-691-08017-8, MR0347778
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324
和書[編集]
入門書[編集]
- 山内恭彦, & 杉浦光夫. (2010). 連続群論入門. 培風館.
- 『群論への30講』 (数学30講シリーズ) (単行本) 志賀浩二 (著) 朝倉書店、ISBN 978-4-254-11483-6
- 稲葉栄次. (1981). 群論入門. 培風館.
- 横田一郎; 初めて学ぶ人のための群論入門, 1997. 現代数学社.
- 代数学1 群論入門 (代数学シリーズ), 雪江明彦, 日本評論社 (2010).
群論と物理学・化学との関係を解説する文献[編集]
- 群と物理, 佐藤光, 丸善出版, 2016年.
- 犬井鉄郎 et. al. (1980). 応用群論-群表現と物理学, 裳華房.
- 今野豊彦. (2001). 物質の対称性と群論. 共立出版.
- 小野田嘉孝. (1996). 物性物理/物性化学のための群論入門, 裳華房.
- 藤永茂, & 成田進. (2001). 化学や物理のためのやさしい群論入門, 岩波書店.
- 中崎昌雄. (1973). 分子の対称と群論, 東京化学同人.
- 高木秀夫. (2018). 量子論に基づく無機化学: 群論からのアプローチ. 名古屋大学出版会.
- F.Albert Cotton. (1990).Chemical Applications of Group Theory, Wiley-Interscience.
関連項目[編集]
外部リンク[編集]
- 群論 (PDF) (信州大学の講義資料)
- 集合から群まで (PDF)
- 1 図形の対称性と群 (PDF)
- 群論入門 group1.pdf group2.pdf group3.pdf group4.pdf group5.pdf group67.pdf (PDF) (茨城大学の講義資料)
- 無機化学 無機化学 IV(J) (PDF) (群論の項)
- 結晶対称性とランダウ理論 (PDF)
- 群論と結晶場 (PDF)
- History of the abstract group concept
- Higher dimensional group theory This presents a view of group theory as level one of a theory which extends in all dimensions and has applications in homotopy theory and to higher dimensional nonabelian methods for local-to-global problems.
- Plus teacher and student package: Group Theory This package brings together all the articles on group theory from Plus, the online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge, exploring applications and recent breakthroughs, and giving explicit definitions and examples of groups.




