角度
角度(かくど、英: measure of angle, angle, plane angle )とは、角(かく、英: angle)の大きさを表す量・測度のことである。
国際単位系におけるSI単位(SI組立単位)はラジアンであり、計量法ではラジアン、度 (角度)、分 (角度)、秒 (角度)、点の5つが法定計量単位となっている。
なお、平面角(en:plane angle)とならんで、これを3次元に拡張した立体角(en:solid angle)もある。
| 平面角(ラジアン) radian | |
|---|---|
| 記号 | rad |
| 系 | 国際単位系 (SI) |
| 種類 | 組立単位 |
| 量 | 平面角 |
| 組立 | m/m |
| 定義 | 円の半径に等しい長さの弧の中心に対する角度[1] |
| 度 (角度) degree | |
|---|---|
| 記号 | ° |
| 系 | 非SI単位 |
| 種類 | SI併用単位 |
| 量 | 平面角、位相角[2] |
| 定義 | 円周を360等分した弧の中心に対する角度[3] |
概要[編集]
一般の平面角の大きさは、単位となる角の大きさの実数倍で表しうる[4]。角およびその角度を表す記号としては ∠ がある。これは角記号(かくきごう、英: angle symbol)と呼ばれる(角度を表す単位記号ではない)。

単に角という場合、多くは平面上の図形に対して定義された平面角(へいめんかく、英: plane angle)を指し、さらに狭義にはある点から伸びる2つの半直線(はんちょくせん、英: ray)によりできる図形を指す。平面角の角度は、同じ端点を持つ2つの半直線の間の隔たりを表す量といえる。2つの半直線が共有する端点は角の頂点(かくのちょうてん、英: vertex of angle)と呼ばれ、頂点を挟む半直線は角の辺(かくのへん、英: side of angle)と呼ばれる[5][6][7]。また、直線以外の曲線や面などの図形がなす角の角度も、何らかの2つの直線のなす角の角度として定義される。より広義には、角は線や面が2つ交わって、その交点や交線の周りにできる図形を指す。線や面が2つ交わって角を作ることを角をなすという。ここでいう面は通常の2次元の面に限らず、一般には超平面である。
角が現れる基本的な図形としては、たとえば三角形や四角形のような多角形(たかくけい、英: polygon)がある。特に三角形は平面図形における最も基本的な図形であり、すべての多角形は三角形の組み合わせによって表現することができる。また、他にも単純な性質を多く持っているため、様々な場面で応用される。有名なものは余弦定理(よげんていり、英: law of cosines)や、三角形の辺の比を通じて定義される三角関数(さんかくかんすう、英: trigonometric function)などがある。余弦定理と三角関数は、三角形の角と辺の間に成り立つ関係を示したもので、これらの関係を利用して、三角形の辺の長さからある角の大きさを求めたり、大きさが既知の角から辺の長さや長さの比を求めることができる。このことはしばしば三角形の合同条件(さんかっけいのごうどうじょうけん、英: congruence condition of triangles)としても言及される。
角度に関連する物理学の概念として、位相(いそう、英: phase)がある。位相は波のような周期的な運動を記述するパラメーターであり、その幾何学的な表現が角度に対応している。位相も角度と同様にラジアンが単位に用いられる。
立体的な角として立体角(りったいかく、英: solid angle)も定義されるが、これは上記の定義には当てはまらない。その大きさは単に立体角と呼ばれることが多く、角度と呼ばれることはほとんどない。
以下、本項目においては平面角を扱う。
定義[編集]
直線のなす角[編集]
1つの定まった値の角度を伴う角とは、平面 α 上の 1 点 O とそれから出る2つの半直線とそれらにより平面 α が分割されて生じる2つの領域の一方 α1 からなる図形と定義できる。ただし後述のように、この定義は数学における主要な定義とは微妙に異なる。
2つの半直線が共有する端点 O を角の頂点、ある角の頂点から出る2つの半直線を角の辺という[5][6][7]。
頂点 O から出る2つの半直線のなす領域 α1 上の、頂点との距離が r 以下の点のみを含む領域を取り出すと、この領域は頂点 O を中心とする半径 r の扇形となる。この扇形の大きさは有限であり、相似な図形の性質から、扇形の弧の長さは半径 r に比例することが知られている。従って、扇形は半径と弧の長さを特定できれば形を完全に特徴づけられるから、半径と弧長を利用して、半径 r を一定に保って弧長を変えた場合に、弧長に比例する量として角度を定義することができる。この場合、弧の長さと半径は比例関係にあるから、単純にその比例係数として角度を定義することができる。すなわち、半径 r, 角度 φ の扇形の弧長が半径 r と角度 φ の積 rφ に等しくなるように角度を定義する。
- 角度 × 半径 = 弧長
この角度の定義は、直接的に半径と弧長の比を用いて表すこともできる。
- 角度 ≔ 弧長/半径
または
- 角度 : 1 = 弧長 : 半径
角度を固定すれば、半径と弧長の比は一定であり、同じ角度を持つ扇形はすべて互いに相似である。従って、はじめに与えた頂点 O を挟む2つの半直線がなす領域 α1 に対しても扇形と同様に角度を与えることができる。すなわち、半直線のなす領域 α1 に対する角度は、その領域に含まれる、頂点 O を共有する扇形の角度に等しい。
上述のように決まった図形に対する角度を定義すれば、図形の変形を特徴づける量としても角度を用いることができる。はじめ、頂点 O を共有する2つの半直線が同じ場所に重なっている状態から、一方の半直線を、その端点を点 O から動かさずにその向きを変えるように動かすと、2つの半直線がなす領域 α1 は半直線の運動に応じて変形される。このとき、領域 α1 の角度の変化量として、動かした半直線の回転角を定義することができる。言い換えると、ある1つの半直線の向きを変えた場合に、変える前と変えた後の位置にある半直線のなす角がその半直線の回転角である。この観点からは角度は2つの半直線の開き具合を示す量ともいえる。実際、このような回転から角および角度を定義している事典もある[8]。
上記の点 O と2つの半直線が定まると、それらにより平面 α が分割されて生じる2つの領域 α1, α2 にそれぞれ対応して2つの角が生じる。この2つの角のうち角度が大きいほうを優角[9][10][11][7][12]、小さいほうを劣角[11][7][13]と呼ぶ。明らかにどんな一組の頂点と2辺についても、その優角と劣角との角度の和は、2π で一定である。
平面 α 上の1点で交わる2つの直線は平面 α を4つの領域に分け、それぞれの領域に対応する4つの角が生じる。これら4つの角を、この2つの直線のなす角という。1点で交わる2つの直線は同一平面上にあるので、"平面上の"という条件は実は必要がない。
ダフィット・ヒルベルトがその著書の『幾何学基礎論』において示した公理系[5]では、「端点を共有する 2つの半直線の組」(引用文献のままの表現ではない)として角を定義しており、日本でもこの主旨の定義を採用している数学辞典[9][6]や国語辞典[11][7][14]が多く、最も受け入れられた数学的定義と見なせる。
この定義の前記定義との違いは 2つの半直線が挟む領域を含めていないことである。ヒルベルトの公理系ではそのかわり、平面 α が角(2つの半直線)により分割されて生じる 2つの領域の一方を角の内部、他方を角の外部として区別している。角度の小さい領域が内部になるのだが、この段階では角度はまだ定義されていないため、別の方法での定義をしている。そして定理20で角の大小関係を定義している。すなわち、1辺を共有する2つの角のうち一方の角 θ1 の辺が他方の角 θ2 の内部にあれば、θ1 < θ2 であると定義する。すなわち、角の大小関係として劣角の角度の大小関係を採用したことになる。
ユークリッドの著作『原論』[15][16][17]では第1巻の定義8において、「互いに交わる2つの線 (line) の傾き (inclination)」(引用文献のままの表現ではない)と定義されている。"傾き" (inclination) という語の解釈次第では2つの直線で分割された領域のいずれかを含むと解釈することも可能であり、そう解釈している辞典もある[18]。またこの定義と同じように「"傾き"である」という定義を採用している国語辞典もある[19]。またこの定義での2つの線は線(原論では定義2)であって直線(原論では定義4)ではないので、曲線も含まれる[15][20]。2つの半直線の傾きとしての角、つまりヒルベルトの定義による角は、定義9で直線角 (rectilinear) という名称で定義されている。
英英辞典には、2つの半直線の間の領域 (space) が角であるとするものもある[21]。
曲線のなす角[編集]
2つの滑らかな曲線が交わるとき、その交点におけるそれぞれの接線同士がなす角を、これらの曲線のなす角という。
平面のなす角[編集]
1つの直線 l で交わる2つの平面 α, β を考える。l 上の任意の1点 A を通り、l に垂直で、それぞれ平面 α および β 上にある直線を考え、この2直線のなす角を、平面 α と β のなす角という。この2直線は点 A で交わるので、角をなし、その角度は点 A を l 上のどこに取っても等しい。平面同士のなす角を二面角 (dihedral angle) ともいう。
角度の計量単位[編集]
角度は、計量法における物象の状態の量の一つである。国際単位系国際文書においては、角度の計量単位であるラジアンが固有の名称と記号を持つ22個のSI単位の一つとなっている。
物理学など自然科学においては、量の次元が重要な役割を果たす。例えば、辺の長さや弧の長さは物理量として「長さ」の次元を持っているが、角度は国際量体系において、辺の長さの比などを通じて定義される無次元量であると位置づけられている。角度が無次元であることは、角度が単位を持たないことを意味しない。
平面上の角度の表し方とその計量単位には、次のものがある。これらは計量法における法定計量単位であり、その定義は、以下のようになっている[22][23]。国際単位系における定義(点 (角度)を除く。)も表現は異なるが、数学的には同じ定義である。
- ラジアン: 円の半径に等しい長さの弧の中心に対する角度
- 度:円周を360等分した弧の中心に対する角度
- 秒:度の3600分の1
- 分:度の60分の1
- 点:度の11.25倍(用途は「航海又は航空に係る角度の計量」に限定される。)
上記のうち、ラジアンのみがSI単位であり、度、秒、分の3つは、非SI単位であるが、SI併用単位である。
法定計量単位ではない計量単位(非法定計量単位)としては、次のものがある。これらを取引・証明に用いることは計量法で禁止されている。
上記の3つの単位は、以下に記する度数法の変種である。
弧度法[編集]

弧度法は扇形に対して、その弧の半径の長さに対する比を以って角の大きさを測る尺度とする。すなわち、弧の長さが半径と等しくなるときの中心角(扇形の要が2つの半径となす劣角)を 1 ラジアン (rad) とする。(radian の訳語として弧度も用いられるが、ラジアンと呼ぶほうが一般的である)。全方位角は 2π ラジアンである。
弧度法は単位円上の弧長で角度の大きさを表したものとも表現できる。あるいは、三角比を含む極限
が成り立つような角度の単位系であると言ってもよい。
度数法の表示と比較して、円周率 π を含むため初学者には親しみにくいが、微分、積分などの解析的操作を行うとき直接扱うことができるという大きな利点があり頻用される。ラジアンは便宜的な単位であり、いつでも外すことができる。すなわち、ラジアンで表された量は換算なしに単位なしの無次元量に置き換えられる。ラジアンを使用する目的は専ら、ある数量が角度を表す量であることを示すためであり、特に必要のない場合は単位なしの無次元量として扱うことが多い。
度数法[編集]
度数法は、平面を定点を端点とする半直線によって 360 等分する時、その等分された一つの角として定まる角度を 1 度 (°) とする単位系である。更に、六十分法を用いて、1° = 60′(分)、1′ = 60″(秒)として下位の単位を定める。定義の仕方から、全方位角は 360°である。
定義から、中心角が 1°の互いに合同な扇形を 360 個張り合わせると扇形の要を中心とする円ができる。円の相似性より、1度を1つの円を 360 個の互いに合同な扇形に分割した時の1つの扇形の中心角の大きさとして定めることもできる。
この体系は、暦における 1年の日数(≒360 日)に由来している。
勾配[編集]
勾配については、水平方向の単位長さに対する垂直方向の長さ(高さ)によって角度を示す方法がある。水平方向に対する垂直方向の長さの割合によって示す方法が道路や鉄道の勾配についてよく行われており、道路については百分率パーセント (%)、鉄道については千分率パーミル (‰) がよく用いられる。例えば「10パーセントの勾配」とは水平方向に100メートル進むと10メートル上昇(または下降)する勾配を示す。45° は100% (1000‰) の勾配になる。尺貫法では、水平方向1尺に対する高さを寸で表したもので勾配を示していた。すなわち、45° の勾配は「10寸」となる。
時間表記[編集]
天文学の分野では時間を使って角度を表すことが多々ある。a 時 b 分 c 秒を ahbmcs と表す。15 倍すれば度数法での表記法と同じになる。
この表記では、分、秒の単位が度数法での名称と同じなので、注意が必要である。
分類[編集]
大きさによる分類[編集]
以下、角度 θ は弧度法で表す。0 から 2π までの大きさの角を、その範囲により次のような名称で呼ぶ。ただし直角には定量的角度を使わない定義があり、ヒルベルトの公理系などで採用されている。
| 範囲 (rad) | 範囲 (°) | 名称 | 読み | 英語 | 一例 |
|---|---|---|---|---|---|
| θ = 0 | θ = 0° | 零角 | れいかく | ||
| 0 < θ < π/2 | 0° < θ < 90° | 鋭角 | えいかく | acute angle | 
|
| θ = π/2 | θ = 90° | 直角 | ちょっかく | right angle | 
|
| π/2 < θ < π | 90° < θ < 180° | 鈍角 | どんかく | obtuse angle | 
|
| θ = π | θ = 180° | 平角 | へいかく | straight angle[10][8] | 
|
| 0 < θ < π | 0 < θ < 180° | 劣角 | れっかく | inferior angle | 
|
| 凸角 | とっかく | ||||
| π < θ < 2π | 180° < θ < 360° | 優角 | ゆうかく | reflex angle[9][10] | 
|
| 凹角 | おうかく | ||||
| 折り返し角 | おりかえしかく | ||||
| θ = 2π | θ = 360° | 周角 | しゅうかく | perigon または round angle[9][10] または full angle[24] | 
|
| 全角 | ぜんかく | ||||
| 全方位角 | ぜんほういかく |
ただし鋭角、直角、鈍角以外の用語はあまり使われない。[要出典]
英語で劣角に対応する用語は不明である。『科学技術45万語和英対訳大辞典』[25]では "inferior angle" という語を当ててはいるが、この語が英語圏で劣角の意味で広く使われている証拠は見つからない。研究社の新英和大辞典[10]では優角を "superior angle" または "major angle" ともいうとの記載はあるが、その反対語となりうる "inferior angle" および "minor angle" についての記載はない。
『図説 数学の事典』[8]では、π < θ < 2π の角を優角ではなく折り返り角と記しているが、原著はドイツ語であり、そこからの翻訳なので英語との対応は不明である。また θ = 2π の角を周角ではなく全角と記している。
角同士の関係による分類[編集]
- 優角・劣角

- 始点を共有する2本の半直線が、平面からその一部を切り取るとき、切り取る部分の小さくない方を優角(ゆうかく、英: major angle)と呼び、そうでない方を劣角(れっかく、英: minor angle)と呼ぶ。優角と劣角の和は、周角に等しい。通常、特に断りのない限り、2本の半直線が成す角とは劣角を指す。なお、2本の半直線が平角をなすとき、特に優角、劣角と区別することはない。
- 余角
- 鋭角に対し、合わせて直角となる角あるいは角度をその角の余角(よかく、英: complementary angle, co-angle)という。
- したがって、角度 に対して余角は の値となる。
- ・ 余弦関数では、。
- 補角
- 平角より小さい角度を持つ角に対し、合わせて平角となる角あるいは角度をその角の補角(ほかく、英: supplementary angle)と呼ぶ。
- したがって、角度 に対しては補角は の値となる。
- ・ 、。
図形との関係による分類[編集]

- 外角・内角
- 多角形において、頂点を共有する2辺の成す角を、内角(ないかく、英: interior angle)と呼ぶ。内角の補角を外角(がいかく、英: exterior angle)と呼ぶ(これら2辺のうち一方を延長して作られる)。
- 多角形の内角の和は、多角形の頂点の数 n の関数であり、その大きさは (n − 2)π に等しい。
- 多角形の外角の和は、多角形の頂点の数 n に関係なく、一定の値 2π に等しい。
- 正 n 角形の1つの内角、外角の大きさは、上のそれぞれの値を n 等分して求められる。
- 錯角・同位角

- 2本の直線を考える。直線の両方と異なる点で交わる第3の直線を引くとき、この直線を横断線(おうだんせん、英: transversal)と呼ぶ。横断線から2本の直線が切り取る線分の両端にそれぞれ4つの角を生ずるが、このとき線分の両端からそれぞれ1つずつの角を選んで作る2つの角の組のうち、
- 横断線の反対側にできる角で、辺の一部を共有する角の組を錯角(さっかく、英: alternate interior angles)、
- 一方の角がその内部に他方を含むような角の組を同位角(どういかく、英: corresponding angles)と呼ぶ。
- 錯角、同位角のいずれか一方が等しければ、他方も等しく、元の2直線は平行線であることが分かる(平行線の成立条件)
- また、元の2直線が平行であるならば、錯角、同位角はそれぞれ互いに等しい大きさを持つ(平行線の性質)。
- 中心角・円周角
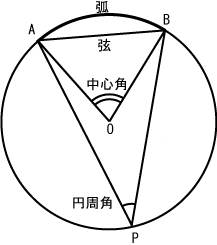
- 扇形の2本の半径のなす角を、中心角(ちゅうしんかく、英: central angle)という。すなわち中心角とは、円の円周から切り取った弧を、その円の中心から見込む角のことである。またこのとき、弧を除く円周上の1点から、弧を見込む角のことを、円周角(えんしゅうかく、英: angle of circumference)という。同じ弧を見込む中心角は、円周角の2倍の大きさを持つ。
- 円周を n 等分して n 本の弧に分けるとき、n 等分点を頂点とする正 n 角形の1つの外角と、n 本の弧の1つを見込む中心角の大きさは等しくなる。
記号[編集]
角を表す記号[編集]
角を表す記号には角記号 ∠ と直角記号 ∟ がある。例えば、頂点 O から出る辺または半直線 Ox, Oy のなす角は ∠xOy または ∠yOx と表される。あるいはより簡単に ∠O と表される場合もある。頂点の周りの角は複数存在するため、頂点やそこから伸びる辺を示しても角を特定することはできないが、文脈上どの角を指しているかが明らかな場合にはこのような省略記法が用いられる。 直角記号についても同様で、示す角が特に直角をなしている場合に、∟xOy や ∟O のように用いられる。
それぞれの記号は角を表すと同時に、その角度を示すためにも用いられる。たとえば三角形 △ABC の内角の和が 180° に等しいことを示す際に、
- ∠ABC + ∠BCA + ∠CAB = 180°
と表すことがある。この場合、それぞれ ∠ABC は頂点 B、∠BCA は頂点 C、∠CAB は頂点 A の周りの内角の大きさを表している。
角度の単位記号[編集]
なお、国際単位系の規定では、一般に、数値と単位記号との間にはスペース(通常は半角スペース en:thin space)を挟むことになっているが、度数法による度・分・秒の場合は、数値と単位記号との間にはスペースを挟まない(度 (角度)#記法)。
- 例:「32.5°」とする。スペースを入れた「32.5 °」の表記は不可。
- 例: 「139°41′56″」とする。スペースを入れた「139 ° 41 ′ 56 ″」の表記は不可。
ラジアンにはSI接頭語を付することができるので、その分量単位と単位記号は、例えば以下のようになる。
- ミリラジアン:mrad
- マイクロラジアン:µrad
- ナノラジアン:nrad
非法定計量単位の単位記号[編集]
非法定計量単位である角度の記号は、通常、次のものが使われている。
角度の計算[編集]
2つの辺のなす角度は、2辺を幾何ベクトルと見なし、2つのベクトルの内積(ないせき、英: inner product)を用いることで計算できる。この方法は言い換えれば、余弦定理を利用して角度を得る方法である。一般の角度を計算するには三角関数の値を求め、その値を逆三角関数に与えることで角度を得る。
それぞれのベクトルを u→, v→ とすると、それらの大きさ |u→|, |v→| は対応する辺の長さを表している。ベクトル u→, v→ の内積 u→ · v→ は、
と表すことができ、θ は2辺のなす劣角の大きさと見なせる。内積 u→ · v→ およびそれぞれのベクトルの絶対値 |u→|, |v→| が分かっているなら、cos θ を求めることができ、これを利用して角度 θ を得ることができる。
により、余弦関数 cos θ が得られれば、その逆関数である逆余弦関数を利用して、
より θ が計算できる。つまり、2辺のなす劣角の大きさは以下のように表される。
また、ベクトル u→, v→ によって作られる三角形を考えると、内積 u→ · v→ はベクトル w→ = u→ − v→ を用いて次のように書き換えられる。
従って、3辺の長さが分かっているなら、それらを用いて角度を計算することができる。
内積 u→ · v→ が 0 の場合については、上述の式から直接角度を求めることはできない。しかし、その場合は一般の場合より簡単に角度を求めることができる。
より、2つのベクトルの大きさがいずれも 0 でない場合には、
となる。角度 θ を 0 ≤ θ ≤ π の範囲に限れば、この条件を満たす角度は、
に限られる。これは、0 でない大きさを持つ2つのベクトルの内積が 0 になる場合、それらが直交していることを示す。ベクトルを図形の辺と見なせば、これは2つの辺のなす角が直角になることに対応する。
換算[編集]
各体系の単位には以下のような相互の関係がある。
- 1 rad = 1
- 2π = 360°, 1 ≒ 57.3°
- 1g = 100cg = 0.9° = 54′ = 3240″
- 1cg = 100cc = 0.009° = 32.40″
- 1cc = 0.01cg = 0.32″
- 6400 mil = 360°
- 1h = 15°, 1m = 15', 1s = 15″
その他の単位同士の換算を下の表にまとめる。各行はある単位角度をそれぞれの単位で表した場合の数値を抜き出したものである。
| - | 単位なし | rad | turn | R | mil | ° | ' | " | g | cg | cc | h | m | s |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1/2π | 2/π | 3 200/π | 180/π | 10 800/π | 648 000/π | 200/π | 20 000/π | 2 000 000/π | 12/π | 720/π | 43 200/π |
| 1 rad | 1 | 1 | 1/2π | 2/π | 3 200/π | 180/π | 10 800/π | 648 000/π | 200/π | 20 000/π | 2 000 000/π | 12/π | 720/π | 43 200/π |
| 1 turn | 2π | 2π | 1 | 4 | 6 400 | 360 | 21 600 | 1 296 000 | 400 | 40 000 | 4 000 000 | 24 | 1440 | 86 400 |
| 1 R | π/2 | π/2 | 1/4 | 1 | 1 600 | 90 | 5 400 | 324 000 | 100 | 10 000 | 1 000 000 | 6 | 360 | 21 600 |
| 1 mil | π/3 200 | π/3 200 | 1/6 400 | 1/1 600 | 1 | 9/160 | 27/8 | 405/2 | 1/16 | 25/4 | 625 | 3/800 | 9/40 | 27/2 |
| 1° | π/180 | π/180 | 1/360 | 1/90 | 160/9 | 1 | 60 | 3 600 | 10/9 | 1 000/9 | 100 000/9 | 1/15 | 4 | 240 |
| 1' | π/10 800 | π/10 800 | 1/2 1600 | 1/5 400 | 8/27 | 1/60 | 1 | 60 | 1/54 | 50/27 | 5 000/27 | 1/900 | 1/15 | 4 |
| 1" | π/648 000 | π/648 000 | 1/1 296 000 | 1/324 000 | 2/405 | 1/3 600 | 1/60 | 1 | 1/3240 | 5/162 | 250/81 | 1/54 000 | 1/900 | 1/15 |
| 1g | π/200 | π/200 | 1/400 | 1/100 | 16 | 9/10 | 54 | 3 240 | 1 | 100 | 10 000 | 3/50 | 18/5 | 216 |
| 1cg | π/20 000 | π/20 000 | 1/40 000 | 1/10 000 | 4/25 | 9/1 000 | 27/50 | 162/5 | 1/100 | 1 | 100 | 3/5 000 | 9/250 | 54/25 |
| 1cc | π/2 000 000 | π/2 000 000 | 1/4 000 000 | 1/1 000 000 | 1/625 | 9/100 000 | 27/5 000 | 81/250 | 1/10 000 | 1/100 | 1 | 3/500 000 | 9/25 000 | 27/1 250 |
| 1h | π/12 | π/12 | 1/24 | 1/6 | 800/3 | 15 | 900 | 54 000 | 50/3 | 5 000/3 | 500 000/3 | 1 | 60 | 3600 |
| 1m | π/720 | π/720 | 1/1 440 | 1/360 | 40/9 | 1/4 | 15 | 900 | 5/18 | 250/9 | 25 000/9 | 1/60 | 1 | 60 |
| 1s | π/43 200 | π/43 200 | 1/86 400 | 1/21 600 | 2/27 | 1/240 | 1/4 | 15 | 1/216 | 25/54 | 1 250/27 | 1/3 600 | 1/60 | 1 |
出典[編集]
- ^ 計量単位令 別表第1 項番8 角度、ラジアン
- ^ 国際単位系国際文書では、「平面角および位相角」(plane and phase angle)としている。
- ^ 計量単位令 別表第1 項番8 角度、度
- ^ 『岩波数学辞典』第 2 版、144頁。
- ^ a b c ヒルベルト『幾何学基礎論』。
- ^ a b c 『岩波数学辞典』第 3 版。
- ^ a b c d e 『日本国語大辞典』第六版。
- ^ a b c Gellert『図説 数学の辞典』。
- ^ a b c d 一松、伊藤『数学辞典』。
- ^ a b c d e 『新英和大辞典』第 6 版。
- ^ a b c 『広辞苑』第五版。
- ^ “優角”, 大辞林 (2 ed.), 三省堂 2008年6月20日閲覧。
- ^ “劣角”, 大辞林 (2 ed.), 三省堂 2008年6月20日閲覧。
- ^ 『大辞泉』。
- ^ a b 『エウクレイデス全集』第1巻。
- ^ 中村『ユークリッド原論』。
- ^ ユークリッド原論のサイト群より。外部リンク参照。
- ^ 『岩波数学入門辞典』。
- ^ 『日本語大辞典』。
- ^ アルトマン 2002, p. 16。
- ^ 『オックスフォード現代英英辞典』第 7 版。
- ^ 計量単位令 別表第1、項番8
- ^ 計量単位令 別表第6、項番6
- ^ Wolfram mathworld より。外部リンク参照。
- ^ 『科学技術45万語英対訳大辞典』。
- ^ 計量単位規則 別表第2、「角度」の欄
- ^ 計量単位規則 別表第4、「航海又は航空に係る角度の計量」の欄
参考文献[編集]
- ヒルベルト, D.『幾何学基礎論』中村幸四郎(訳)、筑摩書房〈ちくま学芸文庫〉、2005年12月。ISBN 4-480-08953-5。
- エウクレイデス『エウクレイデス全集—第 1 巻 (1)』斎藤憲・三浦伸夫(訳)、東京大学出版会、2008年1月。ISBN 978-4-13-065301-5。
- 中村, 幸四郎(著、訳)、寺阪, 英孝『ユークリッド原論—縮刷版』他(訳)、共立出版、1996年6月1日。ISBN 4-320-01513-4。
- アルトマン, B.『数学の創造者—ユークリッド原論の数学』大矢建正(訳)、シュプリンガー・フェアラーク東京、2002年11月。ISBN 4-431-70969-X。
- 数学辞典
- Gellert, W.(編)『図説 数学の事典』藤田宏(訳)、朝倉書店、1992年12月。ISBN 4-254-11051-0。
- 日本数学会『岩波数学辞典』(第 2 版)岩波書店、1975年(原著1968年)。
- 日本数学会『岩波数学辞典』(第 3 版)岩波書店、1985年12月。ISBN 4-00-080016-7。
- 一松, 信、伊藤, 雄二『数学辞典』朝倉書店、1993年6月。ISBN 4-254-11057-X。
- 青本, 和彦、上野, 健爾、加藤, 和也、神保, 道夫『岩波数学入門辞典』岩波書店、2005年9月29日。ISBN 978-4000802093。
- 辞書
- 『広辞苑』(第五版)岩波書店、1998年11月。ISBN 4-00-080112-0。
- 『日本国語大辞典』(第六版)小学館、2001年6月。
- 松村, 明(編)『大辞泉』小学館、1995年11月。ISBN 4-09-501211-0。
- 『日本語大辞典』講談社、1989年11月。ISBN 4-06-121057-2。
- 『大辞林』(第 2 版)三省堂。
- 英和・和英辞書
- 竹林, 滋(編)『新英和大辞典』(第 6 版)研究社、2002年3月。ISBN 4-7674-1026-6。
- Hornby, A. S.(編)『オックスフォード現代英英辞典』(第7版)オックスフォード大学出版局、2005年11月。ISBN 4-01-075292-0。
- 日外アソシエーツ『科学技術45万語和英対訳大辞典』日外アソシエーツ、2001年10月。ISBN 4-8169-1688-1。
関連項目[編集]
外部リンク[編集]
- Weisstein, Eric W. "Angle". mathworld.wolfram.com (英語).
- ユークリッド原論、Clark大学D.E.Joyce教授のサイト
- ユークリッド原論、山口大学渡邉研究室
- ユークリッド原論、元東京大学松原望教授(相関社会科学・統計学専攻)
- ユークリッド原論、九州工業大学情報工学部・藤尾研究室
- 『角度』 - コトバンク
















