弧長
数学において、複雑な形状の曲線(弧状線分)の弧長(こちょう、英: arc length)を決定する問題は、曲線の求長 (rectification) とも呼ばれ、特定の曲線に対する求長法は歴史的に様々なものが考えられてきたが、無限小解析の到来とともに曲線に依らない一般論が導かれ、いくつかの場合にはそこから閉じた形の式が得られる。
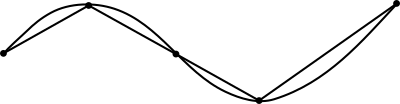
平面内の曲線は、曲線上の有限個の点を線分で結んで得られる折線で近似することができる。各線分の長さは、ユークリッド空間におけるピタゴラスの定理などから直接に求まるので、近似折線の総延長はそれらの線分の長さの総和として決定することができる。
考えている曲線がはじめから折線なのでなければ、用いる線分の長さを短くして数を増やすことによって、よりその曲線に近い形の折線近似が得られる。そうやってよりよい近似折線を次々につくっていくと、その長さは減ることはなく、場合によっては無制限に増加し続ける可能性もある。しかし、殊滑らかな曲線に限っては、それは線分の長さを無限に小さくする極限で必ず一定の極限値へ収斂する。このように、ある種の曲線に対しては、任意の近似折線の長さの上界に最小値 L が存在する。そのとき、その曲線は有限長であるといい、値 L をその曲線の弧長と呼ぶのである。
定義[編集]
X はユークリッド空間 Rn や、より一般の距離空間であるとし、C を空間 X 内の曲線とする。すなわち、C は実数直線内の閉区間 [a, b] から X への連続写像 f : [a, b] → X の像である。
区間 [a, b] に対して 区間の分割
を考えれば、曲線 C 上に有限個の点 f (t0), f (t1), ... , f (tn-1), f (tn) をとることができる。f (ti) から f (ti+1) への距離をそれぞれ d(f (ti)), d(f (ti+1)) で表せば、これはこの2点を結ぶ線分の長さである。
曲線 C の弧長 L = L(C) は
で与えられる。ただし、上限 sup は区間 [a, b] の分割個数 n をいくらでも大きくとってできる分割すべてに亘ってとる。
弧長 L は有限にも無限にもなりうるが、L ≠ ∞ ならば C は有限長(rectifiable; 求長可能)であるといい[注 1]、さもなくば無限長(non-rectifiable; 求長不能)であるという。この弧長の定義において、C は可微分函数 f で定義されている必要はない。実際のところ、一般の距離空間上で考えている場合には、微分可能性を定義することが一般には期待できない。
曲線は様々な方法で媒介変数表示されうる。そこで曲線 C が定義写像 f 以外に媒介変数表示 g: [c, d] → X をも持つ場合を考える。f および g が単射であるときには、連続単調写像 S: [a, b] → [c, d] が存在して、g(S(t)) = f (t) が成り立ち、逆写像 S-1: [c, d] → [a, b] が存在する。明らかに、任意の
の形の和は、ui = S(ti) とおけば、
の形の和に等しく、逆もまた同様である。従って弧長は、それが媒介変数の取り方に依らないという意味で、曲線に内在する性質であることがわかる。
曲線に対するこの弧長の定義は、実数値函数に対する全変分(全変動)の定義の類似である。
積分による弧長の計算[編集]
実函数 f (x) で、f および導函数 f ’ が閉区間 [a, b] 上の連続函数であるようなものを考えると、f のグラフの x = a から x = b までの間の弧長 s は
で与えられる。
曲線が x = X(t), y = Y(t) と媒介変数表示されている場合、f ’(x) = dy/dx = dy/dt / dx/dt であるから
が成り立つ。これらは、十分小さな増分 Δx, Δy に対する距離の公式から求めた式で、Δx, Δy の代わりにその極限を取ったものと考えればわかりよい。
また、極座標系において r = f (θ) で定義された函数の θ = α から θ = β までの間の弧長 s は
で与えられる。
単純曲線まで含めても多くの場合、弧長は閉じた形の式では得られず、積分は数値的に行われることになる。弧長の閉じた形の公式を持つ曲線には、懸垂線、円、擺線、対数螺旋、抛物線、半立方抛物線、直線などが挙げられる。また、楕円の弧長の閉じた形の式を導こうとする試みから、楕円積分の理論が発展した。
線素からの導出[編集]
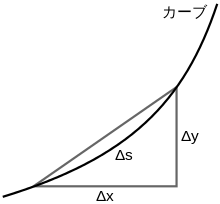
曲線の弧長を近似するために曲線をたくさんの線分に分解するが、弧長の長さを近似値でなく真の値として得るには無限に多くの線分が必要になる。これはつまり、各線分を無限に小さくすることを意味しているが、このことは後に積分を用いる際に効いてくる。
線分の代表元を見れば、その長さ(線素)が微分 ds であることが確認できる。この変位の水平成分を dx、垂直成分を dy で表すと、ピタゴラスの定理から
が従う。曲線が媒介変数 t によって表されているなら弧長は線素 ds を無限小区間 dt に亘って次々に足し合わせればよいから、積分
によって弧長 s が求められる。y が x の函数ならば、t = x として
を得る。これは y = f (x) のグラフの x = a から x = b までの弧長を与えている。
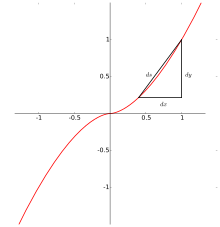
例として、曲線が
で与えられているものとし、さらに t が −1 から 1 までの値をとるものとすると、弧長を表す積分は
となる。数値計算をすれば、この弧長が 2.905 にかなり近いことがわかる。超幾何函数を用いて表せば、
になる。
折線近似からの導出[編集]
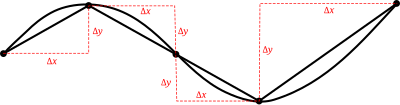
函数 y = f (x) で与えられる曲線が求長可能であるものと仮定する。曲線上の点 a から b までの f に沿った弧長 S を近似するために、斜辺を連結して曲線の弧を「被覆」できるような直角三角形の列を構成する。簡単のため、全ての三角形の底辺は等しく Δx であるものとすると、その各々の三角形に対して高さ Δy が対応づけられて、斜辺の長さがピタゴラスの定理により
と与えられる。S を近似する n 個の斜辺の長さの和は
と書けるが、Δx を小さく取るにつれて近似の精度は上がり、Δx を 0 に近づける極限で S と等しくなる。すなわち、
が得られる。
円弧長[編集]
円弧の長さは中心角を周角で割ったものを周長にかけたものに一致する。半径を r, 直径を d とすると、円の周長は C = 2πr または C = πd である。角度をラジアンで測れば、半径 r, 弧が見込まれる角が θ であるような弧長は s = rθ で与えられる(弧長を s で表すのは、角が弧を「見込む」(subtend) ことに由来する)。特に半円の弧長は s = πr である。s の単位は半径の単位と同じになる。
歴史的方法論[編集]
古代[編集]
数学史の大半の時期においては、偉大な思想家ですらも、特異な弧の長さを計算することは不可能と考えられた。窄出法(積尽法)と呼ばれる独自の方法を用いて、曲線に囲まれる領域の面積を求めた先駆者であったアルキメデスでさえも、直線が持つのと同様の確かな長さを曲線が持つことが可能であるとはほとんど信じていなかった。しばしば微分積分学の起源と考えられるこの分野が開拓される最初の足掛かりは、近似法を用いることであった。人々は、曲線に内接する多角形を考え、その辺の長さを曲線の幾分精密な長さを知るために計算するということを始めるのである。線分の数を増やして各線分の長さを記述することによって、どんどん精密な近似を得ることができた。特に、円に内接する多角形の辺の数を増やすことによって、円周率 π の近似値が求められた。
17世紀[編集]
17世紀には、窄出法を基にして様々な超越曲線に関する幾何学的方法による求長法が導かれた。例えば、対数螺旋は1645年にトリチェリによって(文献によっては1650年代にウォリスによって)、擺線は1658年にレンによって、懸垂線は1691年にライプニッツによって、それぞれ求長されている。
1659年には、ウォリスがウィリアム・ニールによる非自明な代数曲線の最初の求長法の発見と認める、半立方抛物線の求長が成された。
積分公式[編集]
微分積分学が完全に厳密に展開される以前に、弧長に対する現代的な積分公式の基礎は、ファン・ヘラートとフェルマーによって独立に発見される。1659年にファン・ヘラートは、曲線が囲む面積(これは実質的に積分)として弧長が解釈できることを示す構成法を公表し、それを放物線に適用した。一方、1660年にフェルマーは、ヘラートと同じ結果を含むより一般の理論を、著書『De linearum curvarum cum lineis rectis comparatione dissertatio geometrica』(曲線の直線との比較についての幾何学的論述)として出版した。

フェルマーはそれまでの自身による接線を用いる方法に基づいて、曲線
を持つから、接線の方程式は
で与えられる。ここで a を a + ε に変更して、線分 AC が A から D までの曲線の弧長の比較的よい近似になるようにする。線分 AC の長さを求めるためにピタゴラスの定理を用い、
から、両辺の平方根をとって
を得る。弧長を近似するために、フェルマーはこのような小線分の列を足し上げたのである。
無限長曲線[編集]


既に述べたように、曲線の中には求長不能な、すなわち折線近似の長さに上界がない(長さをいくらでも大きくできる)ものが存在する。少し砕けた表現では、そのような曲線は長さが無限大であるなどという。曲線上の(少なくとも二点以上を含む)任意の弧が無限長を持つような連続曲線が存在する。そのような曲線の例としてコッホ曲線や、0 をいずれかの端点とする任意の開区間上で f (x) = xsin(1/x) および f (0) = 0 で定義される函数のグラフなどがある。無限長曲線の大きさを「測る」のには、ハウスドルフ次元やハウスドルフ測度が用いられることもある。
リーマン幾何の場合[編集]
M を(擬)リーマン多様体とし、γ: [0, 1] → M を M 内の曲線、g を(擬)リーマン計量テンソルとすると、曲線 γ の長さは
と定義される。ただし、γ’(t) ∈ Tγ(t)M は γ の t における接ベクトルであり、根号内の符号は与えられた曲線ごとに正方根が実数になることが保証されるほうを選ぶものとする。つまり、空間様曲線に対しては正の符号を、擬リーマン多様体の時間様曲線に対しては負の符号を選ぶことになる。
相対性理論における時間様曲線(世界線)の弧長は、世界線に沿って経過する固有時である。
脚注[編集]
参考文献[編集]
- ^ 一松 信『解析学序説 上巻』裳華房、1981年2月1日、244頁。
- Farouki, Rida T. (1999). Curves from motion, motion from curves. In P-J. Laurent, P. Sablonniere, and L. L. Schumaker (Eds.), Curve and Surface Design: Saint-Malo 1999, pp.63–90, Vanderbilt Univ. Press. ISBN 0-8265-1356-5.
関連項目[編集]
外部リンク[編集]
- Math Before Calculus
- The History of Curvature
- Weisstein, Eric W. "Arc Length". mathworld.wolfram.com (英語).
- Arc Length by Ed Pegg, Jr., The Wolfram Demonstrations Project, 2007.
- Calculus Study Guide – Arc Length (Rectification)
- Famous Curves Index The MacTutor History of Mathematics archive
- Arc Length Approximation by Chad Pierson, Josh Fritz, and Angela Sharp, The Wolfram Demonstrations Project.
- Length of a Curve Experiment Illustrates numerical solution of finding length of a curve.





![{\displaystyle s=\int _{a}^{b}{\sqrt {1+[f'(x)]^{2}}}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c27b05f8c5aa910b4bb893560dd67ff90c00c7fc)
![{\displaystyle {\begin{aligned}s&=\int _{a}^{b}{\sqrt {1+[f'(x)]^{2}}}\,dx\\&=\int _{a}^{b}{\sqrt {1+\left[{\frac {Y'(t)}{X'(t)}}\right]^{2}}}\,dx\\&=\int _{a}^{b}{\frac {1}{X'(t)}}{\sqrt {[X'(t)]^{2}+[Y'(t)]^{2}}}\,dx\\&=\int _{a}^{b}{\sqrt {[X'(t)]^{2}+[Y'(t)]^{2}}}\,dx\cdot {\frac {dt}{dx}}\\&=\int _{X^{-1}(a)}^{X^{-1}(b)}{\sqrt {[X'(t)]^{2}+[Y'(t)]^{2}}}\,dt\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0399f04725f1187d840bdd06f728cb75d5254d4e)









![{\displaystyle S=\lim _{\Delta x_{i}\to 0}\sum _{i=1}^{\infty }{\sqrt {1+{\Bigl (}{\frac {\Delta y_{i}}{\Delta x_{i}}}{\Bigr )}^{\!\!2}}}\,\Delta x_{i}=\int _{a}^{b}{\sqrt {1+{\Bigl (}{\frac {dy}{dx}}{\Bigr )}^{\!\!2}}}\,dx=\int _{a}^{b}{\sqrt {1+[f'(x)]^{2}}}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e26f91dc082db734fb650de01e72ecf0ec5048a)





