ピタゴラスの定理
種類
定理 分野
ユークリッド幾何学 命題
2辺 (a , b c ) 上の正方形の面積に等しくなる。 数式
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
一般化
結果
初等幾何学 におけるピタゴラスの定理 ( ピタゴラスのていり 、( 英 : Pythagorean theorem )は、直角三角形 の3辺 の長さの間に成り立つ関係について述べた定理 である。その関係は、斜辺 の長さを c , 他の2辺の長さを a , b
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}}
という等式 の形で述べられる[1] [2] [3]
現在の日本では三平方の定理 ( さんへいほうのていり ) 勾股弦の定理 ( こうこげんのていり ) ピタゴラス 」と冠しているが、彼が発見したかは定かでない。
ピタゴラスの定理によって、直角三角形において2辺の長さが分かっていれば、残りの1辺の長さを計算することができる[注 1] 直交座標系 において、座標が分かっている2点間の距離 を求めることができる。2点間の距離は、2点の各座標の差の 2乗の総和の平方根 となる[注 2] ユークリッド距離 と呼ばれる。
(a , b , c ) 可算 個あることが知られており、ピタゴラス数 と呼ばれている。
定理の概要 [ 編集 ] 直角三角形において、斜辺 の長さ を c 、直角をはさむ 2辺の長さを a , b 等式 が成り立ち、「ピタゴラスの定理」と呼ばれる:
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
ここで a , b , c
a
=
c
2
−
b
2
{\displaystyle a={\sqrt {c^{2}-b^{2}}}}
b
=
c
2
−
a
2
{\displaystyle b={\sqrt {c^{2}-a^{2}}}}
c
=
a
2
+
b
2
{\displaystyle c={\sqrt {a^{2}+b^{2}}}}
この定理は、余弦定理 によって一般の三角形に拡張される:任意の三角形において、1つの内角の大きさとそれをはさむ2辺の長さから残りの辺(対辺)の長さを計算できる。特にここで考えている内角の大きさが直角の場合、余弦定理はピタゴラスの等式に帰着する。
バビロニア数学 について記された粘土板 プリンプトン322 「ピタゴラス が直角二等辺三角形 のタイルが敷き詰められた床を見ていて、この定理を思いついた」などいくつかの逸話が伝えられているが、実際にピタゴラスが発見したかどうかは正確には判っていない。
ピタゴラスの定理の内容は歴史上の文献にいくつか著されているが、どれだけあるのかは議論がある。ピタゴラスが生まれる前からピタゴラスの定理は広く知られていた。
判明しているもので最初期のものは、ピタゴラスが生まれる1000年以上前のバビロン第1王朝 時代ごろ(紀元前20世紀から16世紀の間)とされる[4] [5] [6] [7]
バビロニアの粘土板 『プリンプトン322 』には、ピタゴラスの定理に関わる要素が数多く含まれている。YBC 7289 の裏面にはそれらしい記述がある。
エジプト数学 やバビロニア数学 などにはピタゴラス数 についての記述があるが、定理を発見していたかまでは定かではない。ただし、直角 を作図するために 3:4:5の直角三角形が作図上利用された可能性がある[8] 古代エジプト エジプト中王国 のパピルス "Berlin Papyrus 6619 (英語版 )
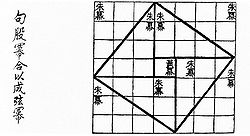
『周髀算経 』におけるピタゴラスの定理の証明(中国語 : 句股冪合以成弦冪 ) 中国古代においては、『周髀算経 』(紀元前2世紀 前後)や『九章算術 』の数学書でもこの定理が取り上げられている。中国ではこの定理を勾股定理 、商高定理 等と呼んで説明している。
紀元前3世紀 に書かれたユークリッド原論 では、第1巻の命題47で言及されている。
インドの紀元前5-8世紀に書かれた『シュルバ・スートラ 』などにも定理に関わる文章が見られる[9] [10]
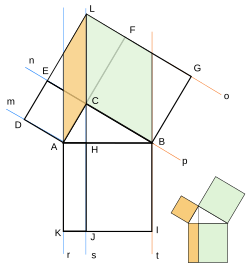
レオナルド・ダ・ヴィンチ によるピタゴラス の定理の証明。橙色の部分を 90 度回転し、緑色の部分は裏返して図の位置にできる。「ピュタゴラス(ピタゴラス)の定理」という呼称が一般的になったのは、西洋においても少なくとも20世紀 に入ってからである[11]
日本での呼称 [ 編集 ] 日本の和算 でも、中国での呼称を用いて鉤股弦の法 ( こうこげんのほう ) [12] [13] a 2 + b 2 = c 2 (a < b < c )a , b , c
日本の明治 時代の中等学校の教科書では「ピュタゴラスの定理」と呼ばれていた。
現在、ピタゴラスの定理は「三平方の定理」とも呼ばれているが、「三平方の定理」と呼ばれるようになったのは1942年 (昭和17年)の太平洋戦争 開始後のことである[11]
このときに「鉤股弦の定理」とする案などもあったが、末綱恕一 (東大教授)の発案で「三平方の定理」に改められたとされる。
ピタゴラス数 [ 編集 ] 3辺の長さが何れも整数である直角三角形 は、ピタゴラスの定理の項目の中で古くから知られた[11] 49612 + 64802 = 81612
a 2 + b 2 = c 2 自然数 の組 (a , b , c ) をピタゴラス数 (Pythagorean triple ) という。特に、a , b , c 互いに素 であるピタゴラス数 (a , b , c ) は原始ピタゴラス数 (primitive Pythagorean triple) と呼ばれる。全てのピタゴラス数は原始ピタゴラス数で (a , b , c ) (ka , kb , kc )
ピタゴラス数 (a , b , c ) が原始的であるためには、3つのうちある2つが互いに素であれば十分である。原始ピタゴラス数の小さい方のリストは、c < 100a < b [14]
(a , b , c ) = (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97) ピタゴラス数の性質 [ 編集 ] ピタゴラス数 (a , b , c )
a または b は 4 の倍数a または b は 3 の倍数a または b または c は 5 の倍数
自然数の組 (a , b , c ) m , n
m , n m > n m と n の偶奇が異なる(一方が偶数 で他方が奇数 )を満たすとして、
(a , b , c ) = (m 2 − n 2 , 2mn , m 2 + n 2 ) (2mn , m 2 − n 2 , m 2 + n 2 ) であることが必要十分である[15] [16] (m , n ) は無数に存在し重複がないので、原始ピタゴラス数は無数に存在し、すべての原始ピタゴラス数を重複なく列挙できる。
例えば
(m , n ) = (2, 1) のとき (a , b , c ) = (3, 4, 5) (m , n ) = (3, 2) のとき (a , b , c ) = (5, 12, 13) (m , n ) = (4, 1) のとき (a , b , c ) = (8, 15, 17) である。a < b a の昇順に並べた一覧表は以下のようになる[17]
原始ピタゴラス数の一覧表
#
m n a b c
1
2
1
3
4
5
2
3
2
5
12
13
3
4
3
7
24
25
4
4
1
8
15
17
5
5
4
9
40
41
6
6
5
11
60
61
7
6
1
12
35
37
8
7
6
13
84
85
9
8
7
15
112
113
10
8
1
16
63
65
11
9
8
17
144
145
12
10
9
19
180
181
13
5
2
20
21
29
14
10
1
20
99
101
15
11
10
21
220
221
16
12
11
23
264
265
17
12
1
24
143
145
18
13
12
25
312
313
19
14
13
27
364
365
20
7
2
28
45
53
21
14
1
28
195
197
22
15
14
29
420
421
23
16
15
31
480
481
24
16
1
32
255
257
25
7
4
33
56
65
#
m n a b c
26
17
16
33
544
545
27
18
17
35
612
613
28
9
2
36
77
85
29
18
1
36
323
325
30
19
18
37
684
685
31
8
5
39
80
89
32
20
19
39
760
761
33
20
1
40
399
401
34
21
20
41
840
841
35
22
21
43
924
925
36
11
2
44
117
125
37
22
1
44
483
485
38
23
22
45
1012
1013
39
24
23
47
1104
1105
40
8
3
48
55
73
41
24
1
48
575
577
42
25
24
49
1200
1201
43
10
7
51
140
149
44
26
25
51
1300
1301
45
13
2
52
165
173
46
26
1
52
675
677
47
27
26
53
1404
1405
48
28
27
55
1512
1513
49
28
1
56
783
785
50
11
8
57
176
185
#
m n a b c
51
29
28
57
1624
1625
52
30
29
59
1740
1741
53
10
3
60
91
109
54
15
2
60
221
229
55
30
1
60
899
901
56
31
30
61
1860
1861
57
32
31
63
1984
1985
58
32
1
64
1023
1025
59
9
4
65
72
97
60
33
32
65
2112
2113
61
34
33
67
2244
2245
62
17
2
68
285
293
63
34
1
68
1155
1157
64
13
10
69
260
269
65
35
34
69
2380
2381
66
36
35
71
2520
2521
67
36
1
72
1295
1297
68
37
36
73
2664
2665
69
14
11
75
308
317
70
38
37
75
2812
2813
71
19
2
76
357
365
72
38
1
76
1443
1445
73
39
38
77
2964
2965
74
40
39
79
3120
3121
75
40
1
80
1599
1601
また、フランスの数学者ピエール・ド・フェルマー は一般のピタゴラス数 (a , b , c ) S = 1 / 2 ab 平方数 でないことを無限降下法 により証明した[18]
Jesmanowicz 予想 [ 編集 ] 1956年に Jesmanowicz が次の予想を提出した:
(a , b , c ) を原始ピタゴラス数、n を自然数とする。方程式:
(
a
n
)
x
+
(
b
n
)
y
=
(
c
n
)
z
{\displaystyle (an)^{x}+(bn)^{y}=(cn)^{z}}
の自然数解 (x , y , z )
x
=
y
=
z
=
2
{\displaystyle x=y=z=2}
のみである。 特別なピタゴラス数 [ 編集 ] 直角をはさむ2辺 a , b (3, 4, 5), (20, 21, 29), (119, 120, 169), … オンライン整数列大辞典 の数列 A114336 )である。この問題はフランスの数学者ピエール・ド・フェルマー が出題し、解も発見した[19] 斜辺 c と他の2辺の和 a + b a = 4565486027761, b = 1061652293520, c = 4687298610289である。この問題はピエール・ド・フェルマーが出題し、解も発見した[20] ピタゴラス数 (a , b , c a , b c が平方数 になるのは (119, 120, 169) [21] 1192 + 1202 = (132 )2 . 3辺の長さが a , b , c a , b , c (135, 352, 377) [22] 一般化 [ 編集 ] 角の一般化 [ 編集 ] 第二余弦定理
c 2 = a 2 + b 2 − 2ab cos C はピタゴラスの定理を C = π / 2 C = 0
指数の一般化 [ 編集 ] 指数の 2 の部分を一般化すると
an + bn = cn となる。n = 2a , b , c 無数に存在する が、n ≥ 3
次元の一般化 [ 編集 ] 3次元空間内に平面があるとき、その閉領域 S の面積は、yz 平面、zx 平面、xy 平面への射影の面積 Sx , Sy , Sz
S
2
=
S
x
2
+
S
y
2
+
S
z
2
{\displaystyle S^{2}={S_{x}}^{2}+{S_{y}}^{2}+{S_{z}}^{2}}
と表される。これは高次元へ一般化できる。
ピタゴラスの定理の証明 [ 編集 ] この定理には数百通りもの異なる証明 がある。
相似による証明 [ 編集 ] 相似を用いた証明 頂点 C から斜辺 AB に下ろした垂線 の足を H とする。△ABC と △ACH は相似 である。ゆえに
AC
:
AH
=
AB
:
AC
⟹
AH
=
AC
×
AC
AB
=
b
2
c
{\displaystyle {\text{AC}}:{\text{AH}}={\text{AB}}:{\text{AC}}\Longrightarrow {\text{AH}}={{\text{AC}}\times {\text{AC}} \over {\text{AB}}}={b^{2} \over c}}
であり、同様に
BH
=
a
2
c
{\displaystyle {\text{BH}}={a^{2} \over c}}
である。したがって
c
=
AH
+
BH
=
b
2
c
+
a
2
c
{\displaystyle c={\text{AH}}+{\text{BH}}={b^{2} \over c}+{a^{2} \over c}}
であるから、両辺に c を掛けて
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}}
を得る。
三角比による証明 [ 編集 ] 前節の証明は、三角比 を用いると簡単に表記できる:
c
2
=
c
×
c
=
c
×
(
AH
+
BH
)
=
c
×
(
b
cos
A
+
a
cos
B
)
=
b
×
c
cos
A
+
a
×
c
cos
B
=
b
×
b
+
a
×
a
=
a
2
+
b
2
.
{\displaystyle {\begin{aligned}c^{2}&=c\times c\\&=c\times ({\text{AH}}+{\text{BH}})\\&=c\times (b\cos A+a\cos B)\\&=b\times c\cos A+a\times c\cos B\\&=b\times b+a\times a\\&=a^{2}+b^{2}.\end{aligned}}}
本証明を一般の三角形に拡張すると、第二余弦定理 の証明が得られる。
外接円を用いた証明 [ 編集 ] 外接円を用いた証明 ∠C = 90° AB を直径とする円O を描くことができる。
このとき点C から直径AB に下ろした垂線の足を H とし、△CHO に対して三平方の定理を証明する。OA = OB = OC = c , CH = a , OH = b
△AHC ∽ △BHC
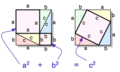
HA : HC = HC : HB (OA − OH) : HC = HC : (OB + OH) (c − b ) : a = a : (c + b ) c 2 − b 2 = a 2 ∴ a 2 + b 2 = c 2 ◾️ 正方形を用いた証明 [ 編集 ] 正方形を用いた証明 △ABC と合同 な4個の三角形を右図のように並べると、外側に一辺が a + b 正方形 (以下「大正方形」)が、内側に一辺が c の正方形(以下「小正方形」)ができる。
(大正方形の面積)=(小正方形の面積)+(直角三角形の面積)× 4 である。大正方形の面積 は (a + b )2 c 2
1
2
a
b
{\displaystyle {\frac {1}{2}}ab}
(
a
+
b
)
2
=
c
2
+
1
2
a
b
×
4
{\displaystyle (a+b)^{2}=c^{2}+{\frac {1}{2}}ab\times 4}
整理して
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
を得る。
正方形を用いた証明の視覚化
正方形を用いた証明2
正方形を用いた証明3
内接円を用いた証明 [ 編集 ] △ABC において、内接円 の半径 r を用いて面積 S を表すと
S
=
1
2
r
(
a
+
b
+
c
)
{\displaystyle S={\frac {1}{2}}r(a+b+c)}
(1 )
となるが、∠C = 90°
S
=
1
2
a
b
{\displaystyle S={\frac {1}{2}}ab}
(2 )
r
=
1
2
(
a
+
b
−
c
)
{\displaystyle r={\frac {1}{2}}(a+b-c)}
(3 )
となるから、(1) (2) (3)
1
2
a
b
=
1
4
(
a
+
b
−
c
)
(
a
+
b
+
c
)
{\displaystyle {\frac {1}{2}}ab={\frac {1}{4}}(a+b-c)(a+b+c)}
整理すると
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
オイラーの公式を用いた証明 [ 編集 ] 三角関数 と指数関数は冪級数 によって定義 されているものとする。(指数法則やオイラーの公式 の証明に本定理が使用されない定義であればよい。)まず sin2 θ + cos2 θ = 1 θ に対して成り立つことを(3通りの方法で)示す。
オイラーの公式より
1
=
e
0
=
e
i
θ
−
i
θ
=
e
i
θ
e
−
i
θ
=
(
cos
θ
+
i
sin
θ
)
(
cos
θ
−
i
sin
θ
)
=
sin
2
θ
+
cos
2
θ
{\displaystyle {\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}}
または
sin
2
θ
+
cos
2
θ
=
(
e
i
θ
−
e
−
i
θ
2
i
)
2
+
(
e
i
θ
+
e
−
i
θ
2
)
2
=
e
2
i
θ
+
e
−
2
i
θ
−
2
−
4
+
e
2
i
θ
+
e
−
2
i
θ
+
2
4
=
1
{\displaystyle {\begin{aligned}\sin ^{2}\theta +\cos ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}+\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}+{\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&=1\end{aligned}}}
もしくは、オイラーの公式から三角関数の半角の公式を導出する。
sin
2
θ
=
(
e
i
θ
−
e
−
i
θ
2
i
)
2
=
e
2
i
θ
+
e
−
2
i
θ
−
2
−
4
=
1
−
cos
2
θ
2
,
cos
2
θ
=
(
e
i
θ
+
e
−
i
θ
2
)
2
=
e
2
i
θ
+
e
−
2
i
θ
+
2
4
=
1
+
cos
2
θ
2
.
{\displaystyle {\begin{aligned}\sin ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}\\&={\frac {1-\cos 2\theta }{2}}\ ,\\\cos ^{2}\theta &=\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {1+\cos 2\theta }{2}}\ .\end{aligned}}}
∴
sin
2
θ
+
cos
2
θ
=
1.
{\displaystyle \therefore \sin ^{2}\theta +\cos ^{2}\theta =1.}
[23] [24]
(1 )
(1) ピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている[25]
(1) 単位円 上において本定理の成立が明らかである。なぜならば、実数の範囲では、単位円上の偏角 θ の点の座標として定義した (cos θ , sin θ ) [26]
前提とした △ABC について、∠A = θ
a
=
c
sin
θ
{\displaystyle a=c\sin \theta }
(2 )
b
=
c
cos
θ
{\displaystyle b=c\cos \theta }
(3 )
(1) (2) (3)
a
2
+
b
2
=
(
c
sin
θ
)
2
+
(
cos
θ
)
2
=
c
2
(
sin
2
θ
+
cos
2
θ
)
=
c
2
⋅
1
=
c
2
{\displaystyle {\begin{aligned}a^{2}+b^{2}&=(c\sin \theta )^{2}+(\cos \theta )^{2}\\&=c^{2}(\sin ^{2}\theta +\cos ^{2}\theta )\\&=c^{2}\cdot 1=c^{2}\end{aligned}}}
ゆえに
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
三角関数の微分公式を用いた証明 [ 編集 ] 正弦および余弦関数を微分すれば
(
sin
θ
)
′
=
cos
θ
{\displaystyle (\sin \theta )'=\cos \theta }
(1 )
(
cos
θ
)
′
=
−
sin
θ
{\displaystyle (\cos \theta )'=-\sin \theta }
(2 )
(1) (2)
(
sin
2
θ
+
cos
2
θ
)
′
=
2
sin
θ
cos
θ
+
2
cos
θ
(
−
sin
θ
)
=
0
{\displaystyle (\sin ^{2}\theta +\cos ^{2}\theta )'=2\sin \theta \cos \theta +2\cos \theta (-\sin \theta )=0}
したがって
sin
2
θ
+
cos
2
θ
=
C
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =C}
ここで C は定数である。θ = 0sin 0 = 0, cos 0 = 1 C = 1
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
(3 )
が得られる[24]
あとは前節と同様にして
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
三角関数の不定積分を用いた証明 [ 編集 ] 下記のように関数を定める。
f
(
θ
)
=
sin
2
θ
+
cos
2
θ
.
{\displaystyle f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta .}
上記を漸化式を利用して不定積分すると
∫
f
(
θ
)
d
θ
=
∫
(
sin
2
θ
)
d
θ
+
∫
(
cos
2
θ
)
d
θ
=
(
1
2
θ
−
1
2
sin
θ
cos
θ
+
C
1
)
+
(
1
2
θ
+
1
2
sin
θ
cos
θ
+
C
2
)
=
θ
+
C
{\displaystyle {\begin{aligned}\int f(\theta )d\theta &=\int (\sin ^{2}\theta )d\theta +\int (\cos ^{2}\theta )d\theta \\&=\left({1 \over 2}\theta -{1 \over 2}\sin \theta \cos \theta +C_{1}\right)+\left({1 \over 2}\theta +{1 \over 2}\sin \theta \cos \theta +C_{2}\right)\\&=\theta +C\end{aligned}}}
である[27] 微分積分学の基本定理 を考慮し、これを微分すると
d
d
θ
∫
f
(
θ
)
d
θ
=
f
(
θ
)
=
d
d
θ
(
θ
+
C
)
=
1
{\displaystyle {\frac {d}{d\theta }}\int f(\theta )d\theta =f(\theta )={\frac {d}{d\theta }}(\theta +C)=1}
である。したがって
f
(
θ
)
=
sin
2
θ
+
cos
2
θ
=
1.
{\displaystyle f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta =1.}
ゆえに、ピタゴラスの定理は成立する。
三角関数の加法定理を用いた証明 [ 編集 ] 三角関数の加法定理は、三平方の定理を使わないで証明できる。本定理を使わないで証明した、三角関数の加法定理を使うと、
cos
2
θ
+
sin
2
θ
=
cos
θ
cos
θ
+
sin
θ
sin
θ
=
cos
(
θ
−
θ
)
=
cos
0
=
1
{\displaystyle {\begin{aligned}\cos ^{2}\theta +\sin ^{2}\theta &=\cos \theta \cos \theta +\sin \theta \sin \theta \\&=\cos(\theta -\theta )\\&=\cos 0=1\end{aligned}}}
または
sin
2
θ
+
cos
2
θ
=
sin
θ
cos
(
π
2
−
θ
)
+
cos
θ
sin
(
π
2
−
θ
)
=
sin
π
2
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =\sin \theta \cos \left({\frac {\pi }{2}}-\theta \right)+\cos \theta \sin \left({\frac {\pi }{2}}-\theta \right)=\sin {\frac {\pi }{2}}=1}
が得られる[28] [29] 半角公式 を適用すると
sin
2
θ
=
1
−
cos
2
θ
2
{\displaystyle \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}}
cos
2
θ
=
1
+
cos
2
θ
2
{\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}}
したがって
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が得られる。
あとはこれまでと同様にして
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる[28]
冪級数展開を用いた証明 [ 編集 ] 三角関数は級数によって定義されているものとし、cos θ と sin θ の自乗をそれぞれ計算すると
sin
2
θ
=
{
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
θ
2
n
+
1
}
2
=
∑
n
=
0
∞
∑
k
=
0
n
(
−
1
)
k
(
2
k
+
1
)
!
(
−
1
)
n
−
k
(
2
n
−
2
k
+
1
)
!
θ
2
n
+
2
=
∑
n
=
0
∞
(
−
1
)
n
θ
2
n
+
2
(
2
n
+
2
)
!
∑
k
=
0
n
(
2
(
n
+
1
)
2
k
+
1
)
=
∑
n
=
1
∞
(
−
1
)
n
−
1
θ
2
n
(
2
n
)
!
∑
k
=
0
n
−
1
(
2
n
2
k
+
1
)
=
−
∑
n
=
1
∞
(
−
1
)
n
θ
2
n
(
2
n
)
!
∑
k
=
0
n
−
1
(
2
n
2
k
+
1
)
cos
2
θ
=
{
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
θ
2
n
}
2
=
∑
n
=
0
∞
∑
k
=
0
n
(
−
1
)
k
(
2
k
)
!
(
−
1
)
n
−
k
(
2
n
−
2
k
)
!
θ
2
n
=
∑
n
=
0
∞
(
−
1
)
n
θ
2
n
(
2
n
)
!
∑
k
=
0
n
(
2
n
2
k
)
=
1
+
∑
n
=
1
∞
(
−
1
)
n
θ
2
n
(
2
n
)
!
∑
k
=
0
n
(
2
n
2
k
)
{\displaystyle {\begin{aligned}\sin ^{2}\theta &=\left\{\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\right\}^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k+1)!}}{\frac {(-1)^{n-k}}{(2n-2k+1)!}}\theta ^{2n+2}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n+2}}{(2n+2)!}}\sum _{k=0}^{n}{\binom {2(n+1)}{2k+1}}\\&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\&=-\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\\cos ^{2}\theta &=\left\{\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}\theta ^{2n}\right\}^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k)!}}{\frac {(-1)^{n-k}}{(2n-2k)!}}\theta ^{2n}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\\&=1+\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\end{aligned}}}
となる[注 3] 二項定理 より
∑
k
=
0
n
(
2
n
2
k
)
−
∑
k
=
0
n
−
1
(
2
n
2
k
+
1
)
=
∑
m
=
0
2
n
(
−
1
)
m
(
2
n
m
)
=
(
1
−
1
)
2
n
=
0
{\displaystyle {\begin{aligned}\sum _{k=0}^{n}{\binom {2n}{2k}}-\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}&=\sum _{m=0}^{2n}(-1)^{m}{2n \choose m}\\&=(1-1)^{2n}=0\end{aligned}}}
である。したがって
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が得られる。
あとはこれまでと同様にして
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる[30]
回転行列を用いた証明 [ 編集 ] 平面において原点を中心とする角 θ の回転 の表現行列は
R
(
θ
)
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
{\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}
であるが、このことも三平方の定理を用いないで証明が可能である。
R (θ ) R (−θ ) = I 2 単位行列 )であるが[31]
R
(
θ
)
⋅
R
(
−
θ
)
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
[
cos
θ
sin
θ
−
sin
θ
cos
θ
]
=
[
cos
2
θ
+
sin
2
θ
cos
θ
sin
θ
−
sin
θ
cos
θ
sin
θ
cos
θ
−
cos
θ
sin
θ
sin
2
θ
+
cos
2
θ
]
=
[
sin
2
θ
+
cos
2
θ
0
0
sin
2
θ
+
cos
2
θ
]
{\displaystyle {\begin{aligned}R(\theta )\cdot R(-\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{bmatrix}}\\&={\begin{bmatrix}\cos ^{2}\theta +\sin ^{2}\theta &\cos \theta \sin \theta -\sin \theta \cos \theta \\\sin \theta \cos \theta -\cos \theta \sin \theta &\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\\&={\begin{bmatrix}\sin ^{2}\theta +\cos ^{2}\theta &0\\0&\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\end{aligned}}}
となる[32]
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が得られる[33]
あとはこれまでと同様にして
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
三角関数と双曲線関数を用いた証明 [ 編集 ] 任意の z ∈ C
sin
2
i
z
+
cos
2
i
z
=
(
i
sinh
z
)
2
+
cosh
2
z
=
cosh
2
z
−
sinh
2
z
=
1
{\displaystyle {\begin{aligned}\sin ^{2}iz+\cos ^{2}iz&=(i\sinh z)^{2}+\cosh ^{2}z\\&=\cosh ^{2}z-\sinh ^{2}z\\&=1\end{aligned}}}
である[34] [35] θ ∈ C
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が成り立つ。
あとはこれまでと同様にして
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
ピタゴラスの定理の逆 [ 編集 ] ピタゴラスの定理は、逆 も真となる。すなわち、△ABC に対して
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
が成立すれば、△ABC は ∠C = π / 2
ピタゴラスの定理に依存しない証明 [ 編集 ] ピタゴラスの定理に依存しない証明 △ABC が a 2 + b 2 = c 2 AB を b 2 : a 2 D とすると
AD
=
c
×
b
2
b
2
+
a
2
=
c
×
b
2
c
2
=
b
2
c
{\displaystyle {\begin{aligned}{\text{AD}}&=c\times {\frac {b^{2}}{b^{2}+a^{2}}}\\&=c\times {\frac {b^{2}}{c^{2}}}\\&={\frac {b^{2}}{c}}\end{aligned}}}
である。これより
AC
:
AD
=
b
:
b
2
c
=
c
:
b
=
AB
:
AC
{\displaystyle {\text{AC}}:{\text{AD}}=b:{\frac {b^{2}}{c}}=c:b={\text{AB}}:{\text{AC}}}
であるから2辺比夾角相等 より
△
ACD
∼
△
ABC
{\displaystyle \triangle {\text{ACD}}\sim \triangle {\text{ABC}}}
∴
∠
ADC
=
∠
ACB
{\displaystyle \therefore \angle {\text{ADC}}=\angle {\text{ACB}}}
同様に
∠
BDC
=
∠
BCA
{\displaystyle \angle {\text{BDC}}=\angle {\text{BCA}}}
となるから
∠
ADC
=
∠
ACB
=
∠
BDC
{\displaystyle \angle {\text{ADC}}=\angle {\text{ACB}}=\angle {\text{BDC}}}
(1 )
となる。
(1)
∠
ADC
=
∠
BDC
{\displaystyle \angle {\text{ADC}}=\angle {\text{BDC}}}
(2 )
一方
∠
ADC
+
∠
BDC
=
π
{\displaystyle \angle {\text{ADC}}+\angle {\text{BDC}}=\pi }
(3 )
であるから、(2) (3)
∠
ADC
=
∠
BDC
=
π
2
{\displaystyle \angle {\text{ADC}}=\angle {\text{BDC}}={\frac {\pi }{2}}}
(4 )
(1) (4)
∠
ACB
=
π
2
{\displaystyle \angle {\text{ACB}}={\frac {\pi }{2}}}
ゆえに △ABC は ∠C = π / 2 [26]
同一法を用いた証明 [ 編集 ] ピタゴラスの定理を用いた証明 B'C' = a , A'C' = b ,∠C' = π / 2 A'B'C' において、A'B' = c'
a
2
+
b
2
=
c
′
2
{\displaystyle a^{2}+b^{2}=c'\,^{2}}
(1 )
が成り立つ。
一方、仮定から △ABC において
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
(2 )
が成り立っている。(1) (2)
c
2
=
c
′
2
{\displaystyle c^{2}=c'\,^{2}}
c > 0, c' > 0
c
=
c
′
{\displaystyle c=c'}
したがって、3辺相等 から
△
ABC
≡
△
A
′
B
′
C
′
{\displaystyle \triangle {\text{ABC}}\equiv \triangle {\text{A}}'{\text{B}}'{\text{C}}'}
∴ ∠C = ∠C' = π / 2 △ABC は ∠C = π / 2 [26]
対偶を用いた証明 [ 編集 ] △ABC において ∠C ≠ π / 2 A から直線 BC に下ろした垂線の足を D とし、AD = h , CD = d
∠C < π / 2 の場合、直角三角形 ABD においてピタゴラスの定理より
c
2
=
(
a
−
d
)
2
+
h
2
=
a
2
−
2
a
d
+
d
2
+
h
2
{\displaystyle {\begin{aligned}c^{2}&=(a-d)^{2}+h^{2}\\&=a^{2}-2ad+d^{2}+h^{2}\end{aligned}}}
であり、同様に直角三角形 ACD では
b
2
=
d
2
+
h
2
{\displaystyle b^{2}=d^{2}+h^{2}}
である。よって
c
2
=
a
2
−
2
a
d
+
b
2
<
a
2
+
b
2
{\displaystyle c^{2}=a^{2}-2ad+b^{2}<a^{2}+b^{2}}
となる。
∠C > π / 2 の場合も同様に考えて
c
2
=
(
a
+
d
)
2
+
h
2
=
a
2
+
2
a
d
+
d
2
+
h
2
=
a
2
+
2
a
d
+
b
2
{\displaystyle {\begin{aligned}c^{2}&=(a+d)^{2}+h^{2}\\&=a^{2}+2ad+d^{2}+h^{2}\\&=a^{2}+2ad+b^{2}\end{aligned}}}
ゆえに
c
2
>
a
2
+
b
2
{\displaystyle c^{2}>a^{2}+b^{2}}
となる。
よっていずれの場合も
a
2
+
b
2
≠
c
2
{\displaystyle a^{2}+b^{2}\neq c^{2}}
である。対偶を取って、a 2 + b 2 = c 2 ∠C = π / 2
なお、この証明から分かるように、
∠C < π / 2 a 2 + b 2 > c 2 ∠C = π / 2 a 2 + b 2 = c 2 ∠C > π / 2 a 2 + b 2 < c 2 という対応がある。
余弦定理を用いた証明 [ 編集 ] 余弦定理を用いた証明 ピタゴラスの定理は既知とすると、それより導かれる余弦定理 を用いることができる。△ABC において、a = BC, b = CA, c = AB, C = ∠ACB
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C}
一方、仮定より
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
であるから
cos
C
=
0
{\displaystyle \cos C=0}
となる。三角形の内角の和は π であるから 0 < C < π
C
=
cos
−
1
0
=
π
2
{\displaystyle C=\cos ^{-1}0={\frac {\pi }{2}}}
ゆえに △ABC は ∠C = π / 2
ベクトルを用いた証明 [ 編集 ] △ABC において
‖
c
→
‖
2
=
‖
a
→
‖
2
+
‖
b
→
‖
2
{\displaystyle \Vert {\vec {c}}\|^{2}=\Vert {\vec {a}}\|^{2}+\Vert {\vec {b}}\|^{2}}
であり
c
→
=
b
→
−
a
→
{\displaystyle {\vec {c}}={\vec {b}}-{\vec {a}}}
である。
ここで
‖
c
→
‖
2
=
c
→
⋅
c
→
=
(
b
→
−
a
→
)
⋅
(
b
→
−
a
→
)
=
‖
b
→
‖
2
−
2
b
→
⋅
a
→
+
‖
a
→
‖
2
{\displaystyle {\begin{aligned}\Vert {\vec {c}}\|^{2}&={\vec {c}}\cdot {\vec {c}}\\&=({\vec {b}}-{\vec {a}})\cdot ({\vec {b}}-{\vec {a}})\\&=\Vert {\vec {b}}\|^{2}-2{\vec {b}}\cdot {\vec {a}}+\Vert {\vec {a}}\|^{2}\\\end{aligned}}}
である。したがって
b
→
⋅
a
→
=
0
{\displaystyle {\vec {b}}\cdot {\vec {a}}=0}
である。よって
∠
C
=
π
2
{\displaystyle \angle {\text{C}}={\frac {\pi }{2}}}
である。ゆえに、ピタゴラスの定理の逆が証明された。
^ 故に (a , b , c ) 自由度 は2次元である。
^ 2次元直交座標系においては、原点O(0, 0) と点P(x , y ) の距離は √ x 2 + y 2 √ は負でない平方根 を表す。
^ 級数の収束半径は ∞ であるからこれは任意の複素数 θ に対して成り立つ。
^ 大矢真一『ピタゴラスの定理 』東海大学出版会〈Tokai library〉、2001年8月。ISBN 4-486-01558-4 。http://www.press.tokai.ac.jp/bookdetail.jsp?isbn_code=ISBN978-4-486-01558-1 。 ^ 大矢真一『ピタゴラスの定理』東海大学出版会〈東海科学選書〉、1975年。 ^ 大矢真一 『ピタゴラスの定理』東海書房、1952年。 ^ Neugebauer 1969 : p.36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."^ Friberg, Jöran (1981). “Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations” . Historia Mathematica 8 : 277-318. doi :10.1016/0315-0860(81)90069-0 . https://www.researchgate.net/publication/222892801 . ^ Høyrup, Jens [in 英語] . "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics". In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF) . Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407.To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db2 -146, somewhere between 2300 and 1825 BC." (IM 67118 (英語版 ) 2 -146) is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)^ Robson, E. (2008). Mathematics in Ancient Iraq: A Social History . Princeton University Press ^ 亀井喜久男. “エジプトひもで古代文明に挑戦しよう ”. 2008年3月3日 閲覧。 ^ Kim Plofker (2009). Mathematics in India . Princeton University Press. pp. 17–18 . ISBN 978-0-691-12067-6 ^ Carl Benjamin Boyer ; Uta C. Merzbach (2011). “China and India” . A history of mathematics (3rd ed.). Wiley. p. 229. ISBN 978-0470525487 . https://books.google.com/books?id=bR9HAAAAQBAJ . "Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements . (...)" ^ a b c 片野善一郎『数学用語と記号ものがたり』裳華房 、2003年8月25日、157頁。
^ コラム ピタゴラスの定理 江戸の数学 国立国会図書館^ 金光三男、安井孜、花木良、河上哲、山中聡恵「教師に必要な数学的素養の育成 : 教科内容の背景にある数学 (数学教師に必要な数学能力に関連する諸問題) 」『数理解析研究所講究録』第1828巻、京都大学数理解析研究所、2013年3月、101-130頁、CRID 1050282810781995008 、hdl :2433/194793 ISSN 1880-2818 。 ^ a の順序はオンライン整数列大辞典 の数列 A020884 による。b , c オンライン整数列大辞典 の数列 A020883 およびオンライン整数列大辞典 の数列 A020882 になる。^ 足立 (1995 , pp. 31–34, 106–109)^ 足立 (2006 , pp. 19–22, 49–55)^ a の順序はオンライン整数列大辞典 の数列 A020884 による。^ 足立 (2006 , pp. 93–95, 99–101)、高瀬 (2019 , pp. 114–115, 180)^ 高瀬 (2019 , pp. 99–101, 147–149)^ 高瀬 (2019 , pp. 151, 174–177)、オンライン整数列大辞典 の数列 A166930 を参照。ただしオンライン数列内のコメント内にある a の値が間違っているので注意が必要。^ 『数学セミナー』通巻673号、日本評論社、2017年11月、52頁。 ^ 世界に1つだけの三角形の組 慶應義塾大学理工学部KiPAS、2018年9月12日^ 稲津將. “オイラーの公式 ”. 2014年10月4日 閲覧。 ^ a b 新関章三(元高知大学)、矢野忠(元愛媛大学). “数学・物理通信 ”. 2014年10月4日 閲覧。
^ Leff, Lawrence S. (2005). PreCalculus the Easy Way ISBN 0-7641-2892-2 . https://books.google.co.jp/books?id=y_7yrqrHTb4C&pg=PA296&redir_esc=y&hl=ja ^ a b c “三平方の定理の逆の証明 ”. 2014年10月8日 閲覧。
^ 不定積分の漸化式 ^ a b “三平方の定理の証明 ”. 2014年10月5日 閲覧。
^ “Einige spezielle Funktionen ”. 2014年11月26日 閲覧。 ^ Hamilton, James Douglas (1994). “Power series”. Time series analysis . Princeton University Press. p. 714. ISBN 0-691-04289-6 ^ “行列と1次変換 ”. 2014年11月22日 閲覧。 ^ “対称行列と直交行列 ”. 2014年11月20日 閲覧。 ^ “Solution for Assignment ”. 2014年11月20日 閲覧。 ^ “双曲線関数について ”. 2014年11月22日 閲覧。 ^ “Complex Analysis Solutions ”. 2014年11月22日 閲覧。
参考文献 [ 編集 ] 関連項目 [ 編集 ] 外部リンク [ 編集 ]