垂直

垂直(すいちょく、英: perpendicular[注釈 1])であること、すなわち垂直性 (perpendicularity) はある一方の直線を適当に平行移動させた時、直角に交わる二つの直線の間の関係性を言う。つまり、その2直線が交わっても、ねじれでも垂直の場合がある。但し、中学校までは、交わる場合のみを扱うことが多い。この性質は関連するほかの幾何学的対象に対しても拡張される。
垂線 (perpendicular[注釈 1]) に関連して垂線の「足」("foot") という術語がしばしば用いられる。考える図形の向きは如何様にも変えることができるから、足と謂えどもそれが必ずしも図形の下方にあるわけではない。
垂直性はより一般の数学概念である直交性の特別の場合と考えられる。すなわち、垂直性とは古典的な幾何学的対象に関する直交性を言うものである。ゆえに、より進んだ数学において、より複雑な幾何学的直交性(例えば曲面とその法線の関係など)に対して「垂直」あるいは「垂線」のような語を用いることもある[2]。
定義[編集]
「二つの直線が互いに垂直」であるとは、それら二つの直線のある一方を適当に平行移動させた時、直角を成すときにいう[3]。
このとき、前者の直線が後者に対して垂直ならば後者の直線も前者に対して垂直となるという意味において、垂直性は対称的であり、そういった理由から(どれが何に対してというような限定を抜きにして)これら二直線は(互いに)垂直であるという風にも言うことができる。
- 垂直性を線分や半直線に対して定めるのは容易である。たとえば、線分 AB が線分 CD に垂直であるとは、両線分をそれぞれ両方向に無限に延長して直線にするとき、直線 AB が直線 CD に対して(上で述べた意味で)垂直であることを言う。これを記号 AB ⊥ CD であらわす[3]。
- 与えられた直線が平面に対して垂直であるとは、その平面上にありかつそれらの交点を通る任意の直線に対して与えられた直線が垂直となるときに言う。これもまた直線の間の垂直性の定義に依存するものである。
- 二つの平面が垂直であるとは、それらの成す二面角が直角となるときに言う。
垂線の作図[編集]
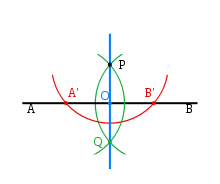
点 P を通り直線 AB に垂直な直線の定木とコンパスを用いた作図は以下のようにする[4]:
- Step 1 (赤): 点 P を中心とする円を作図して、直線 AB 上に P から等距離にある二点 A', B' を取る。
- Step 2 (緑): A', B' の各点を中心とする同半径の円を作図して、その二円の交点 Q, R を取る。
- Step 3 (青): 二点 Q, R を結べばそれが所期の垂線 PQ である。
この PQ が AB に垂直であることを見るには、△QPA' と △QPB' に対して三辺相等 (SSS) の条件が成り立つことにより、∠OPA' と ∠OPB' が等しいことを知ればよい。そうすれば △OPA' と △OPB' に対して二辺夾角相等 (SAS) の条件が成り立つから、∠POA と ∠POB が等しい。

点 P を通る直線 g に対する垂線を得るために(円周角に関する)タレスの定理を利用することができる。
直角の作図法の基礎としてピュタゴラスの定理を用いることができる。例えば、長さの比が 3 : 4 : 5 となるような棒を節で繋いだ鎖を使って三角形を作れば、一番長い辺の対角が直角になる。
関連項目[編集]
注[編集]
注釈[編集]
出典[編集]
- ^ Kay (1969, p. 114)
- ^ 例えば normal of plane - PlanetMath.(英語)
- ^ a b Kay (1969, p. 91)
- ^ compass and straightedge construction of perpendicular - PlanetMath.(英語)
参考文献[編集]
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52--13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69--12075
外部リンク[編集]
- Weisstein, Eric W. "Perpendicular". mathworld.wolfram.com (英語).
- perpendicularity in Euclidean plane - PlanetMath.org(英語)
