二面角

二面角(にめんかく、英: dihedral angle)は、2つの平面(またはその部分集合)がなす角度である。たとえば、二面角が0なら2面は平行(同一の場合を含む)で、π/2(90°)なら垂直である。
二面角は、法線同士の角度として定義される。つまり、2面の法線ベクトルをa、bとすると二面角 φ は
で表せる。二面角は2π(360°)の周期性を除いて一意には定まらないが、通常は主値として0~π(180°)の範囲で表す。ただし、多面体の面で内側と外側を区別する場合などでは、0~360°の範囲で表す。また、内側・外側も面の向きも区別しない場合は、
と絶対値を取り、0~π/2(90°)の範囲で表す。2つの平面は鋭角と鈍角の2つの角度を為すので、そのうち鋭角のほうを取っていることになる。
二面角は、2面に垂直な平面(平行移動の自由度を残して決まる)での断面内で考えると、通常の直線同士の角度に還元できる。面の断面は直線なので、断面の2直線がなす角度が2面の二面角である。
二面角は、3つの(零でない)ベクトルa、b、cに対しても定義でき、面ab(ベクトルaとbが張る面)と面bcの二面角を考える。また、4つの(異なる)点A・B・C・Dについても、面ABCと面BCDの二面角を考える。面ABCと面BCDの二面角が0でない場合、直線ABと直線CDはねじれの位置にある。このため、ねじれ角(torsion angle)ともいう。
多面体[編集]
多面体では、辺で隣り合う2面の二面角を考える。(単に二面角といった場合は、それ以外の二面角は無視する)凸多面体は、全ての(中心側の)二面角が180°未満の多面体であると定義される。正多面体と準正多面体(半正多面体の特殊例)は、全ての二面角が等しい。このほかに、それらの変形(立方体の変形の直方体など)でもそれは成り立つ。
| 多面体名 | 面形状 | 面数 | 二面角 | (面間) |
|---|---|---|---|---|
| 正四面体 | 正三角形 | 4 | 70.52 | |
| 立方体 | 正方形 | 6 | 90 | |
| 正八面体 | 正三角形 | 8 | 109.47 | |
| 正十二面体 | 正五角形 | 12 | 116.56 | |
| 正二十面体 | 正三角形 | 20 | 138.18 | |
| 立方八面体 | 正三角形 | 8 | 125.26 | (3-4) |
| 正方形 | 6 | |||
| 二十・十二面体 | 正三角形 | 20 | 142.62 | (3-5) |
| 正五角形 | 12 | |||
| 切頂四面体 | 正三角形 | 4 | 109.47 | (3-6) |
| 正六角形 | 4 | 70.52 | (6-6) | |
| 切頂立方体 | 正三角形 | 8 | 125.26 | (3-8) |
| 正八角形 | 6 | 90 | (8-8) | |
| 切頂八面体 | 正方形 | 6 | 125.26 | (4-6) |
| 正六角形 | 8 | 109.47 | (6-6) | |
| 切頂十二面体 | 正三角形 | 20 | 142.62 | (3-10) |
| 正十角形 | 12 | 116.56 | (10-10) | |
| 切頂二十面体 | 正五角形 | 12 | 142.62 | (5-6) |
| 正六角形 | 20 | 138.18 | (6-6) | |
| 小菱形立方八面体 | 正三角形 | 8 | 144.73 | (3-4) |
| 正方形 | 18 | 135 | (4-4) | |
| 大菱形立方八面体 | 正方形 | 12 | 144.73 | (4-6) |
| 正六角形 | 8 | 135 | (4-8) | |
| 正八角形 | 6 | 125.26 | (6-8) | |
| 小菱形二十・十二面体 | 正三角形 | 20 | 159.09 | (3-4) |
| 正方形 | 30 | |||
| 正五角形 | 12 | 148.28 | (4-5) | |
| 大菱形二十・十二面体 | 正方形 | 30 | 159.09 | (4-6) |
| 正六角形 | 20 | 148.28 | (4-10) | |
| 正十角形 | 12 | 142.62 | (6-10) | |
| ねじれ立方体 | 正三角形 | 32 | 153.23 | (3-3) |
| 正方形 | 6 | 142.98 | (3-4) | |
| ねじれ十二面体 | 正三角形 | 80 | 164.17 | (3-3) |
| 正五角形 | 12 | 152.93 | (3-5) |
化学[編集]
化学において、二面角とは2原子を共有した2組の3原子を通る面の間の角度である。化学では、原子がA-B-C-Dと結合しているときの二面角が、立体配座を決定する要素のひとつとして重要である。二面角は結合距離や結合角に比べ自由度が大きいため、特に比較的大きな有機化合物においては全体構造を決定する重要な要素である。
定義[編集]
二面角は2つの交差する面の間の、交線に垂直な3つ目の面上での角度である[1]。
ねじれ角(torsion angle[2])は二面角の一例であり、立体化学において化学結合によって連結された分子の2つの部分の幾何的関係を定義するために使われる。
立体化学における二面角[編集]
|
|

|
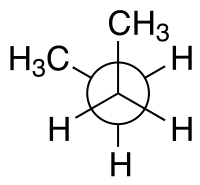
| 配置の名称 | syn n-ブタン ニューマン投影式 |
syn n-ブタン のこぎり台投影式 |

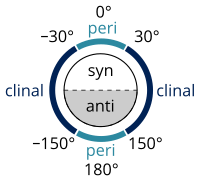
立体化学において、例えば X…A-B…Y (…は任意の結合次数を持つ結合)のような単結合を持つ分子には、A-B 結合回りの立体配座が異る立体異性体が存在する。この異性体を区別するため、X, A, B の成す平面と A, B, Y の成す平面との間の二面角を用いることができる[3]。0°と±90°の間の角度に対応する立体化学配置はシン(syn、s)と呼ばれ、±90°と±180°の間の角度に対応する配置はアンチ(anti、a)と呼ばれる。同様に、30°と150°あるいは−30°と−150°の間の角度に対応する配置はクリナル(clinal、c、反っているの意)、0°と±30°あるいは±150°と±180°の間はペリプラナー(periplanar、p、平面に近いの意)と呼ばれる。
これら2種類の用語を組み合わせて角度の4つの領域を定義できる。0°から±30°はシンペリプラナー(sp)、30°から90°および−30°から−90°はシンクリナル(sc)、90°から150°および−90°から−150°はアンチクリナル(ac)、±150°から180°はアンチペリプラナー(ap)である。シンペリプラナー配座はシン (syn-) あるいはシス(cis-)配座、アンチペリプラナーはアンチ(anti)あるいはトランス(trans)、シンクリナルはゴーシュ(gauche)あるいはスキュー(skew)とも呼ばれる。
例えば、n-ブタンでは、2つの中心炭素原子と両端のメチル基の炭素原子の一方の観点から2つの面を特定することができる。上に示されている二面角60°のシン配座は二面角180°のアンチ配座よりも不安定である。
高分子では、記号T、C、G+、G−、A+、A−が推奨される(それぞれap、sp、+sc、-sc、+ac、-acに対応する)。
タンパク質の二面角[編集]

1963年にG・N・ラマチャンドラン、C・ラマクリシュナン、V・サシセカランによって開発された[4]ラマチャンドラン・プロットはタンパク質構造中のアミノ酸残基の主鎖の二面角 φ に対してエネルギー的に許容される角度 ψ の領域を可視化する方法である。右の図は主鎖の二面角 φ および ψ の定義を表わしている[5]。
タンパク質鎖では、図に示されているように3つの二面角 φ(ファイ)、 ψ (プサイ)、 ω (オメガ)が定義される。ペプチド結合の平面性によって、 ω は180°(典型的なトランス配座)あるいは0°(稀なシス配座)に大抵制限される。トランスおよびシス異性体におけるCα原子間の距離はそれぞれ約3.8, 2.9 Åである。シス異性体は主に、Xaa-Proペプチド結合(Xaaは任意のアミノ酸)において観察される。
側鎖の二面角は180°、60°、−60°近くに集まる傾向にあり、それぞれトランス、ゴーシュ+、ゴーシュ−配座と呼ばれる。特定の側鎖の二面角の安定性は隣接した主鎖および側鎖の二面角によって影響される。例えば、原子同士の衝突が増大するためゴーシュ+配座の次にゴーシュ+配座が続くのは稀である。
脚注[編集]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). オンライン版: (2006-) "dihedral angle".
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). オンライン版: (2006-) "torsion angle".
- ^ Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313
- ^ Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. (1963). “Stereochemistry of polypeptide chain configurations”. Journal of Molecular Biology 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.
- ^ Richardson, J.S. (1981). “Anatomy and Taxonomy of Protein Structures”. Advances in Protein Chemistry. Advances in Protein Chemistry 34: 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.


