平行

初等幾何学、特にユークリッド幾何学における平行性(へいこうせい、英: parallelism)は、ユークリッド平面上の直線が互いに交わらないという関係性を抽象化するものである。三次元空間において、直線と平面や平面同士についても共有点がないことを以って平行性を考えることができる。ただし、三次元空間内の直線同士の場合には、それらが互いに平行となるためには共面性(それらが同一平面上にあること)を要請しなければならない(交わらない二直線は、それらが同一平面上にないならばねじれの位置にあるという)。
平行線はユークリッド原論における平行線公準の主対象である[注釈 1]。 平行性は第一義にはアフィン幾何学の性質の一つであり、ユークリッド幾何学はその種の幾何学の特別な実例である。その他の幾何学においては、例えば双曲幾何学などでは、同様の(しかしまったく同じではない)特定の性質を満たすことを「平行」と言い表す。
以下、特に言及のない限り、主にユークリッド幾何学における平行性について述べる。
歴史[編集]
平面上の互いに交わらない直線の対としての平行線の定義は『原論』第 I 巻の定義 23 に現れている[1]。古代ギリシア人は、おもに平行線公準を証明しようと試みる中で、もっと別の平行線の定義についても議論している。プロクルスは等距離直線としての平行線の定義はポセイドニオスに帰するとし、同じ脈絡においてゲミノスを引用している。シンプリキオスもポセイドニオスの定義に言及し、アガニスによるその修正についても述べている[1]。
19世紀の終わりごろ、イングランドにおいて『原論』はいまだ中学校における標準的な教科書であった。新たな射影幾何学および非ユークリッド幾何学の勃興により、旧来からの幾何学の取り扱いは変化を余儀なくされており、このころいくつか新しい幾何学の教科書が書かれている。これら新興の教科書における主要な相違点は—それら新興教科書の間でも、またそれらと原論との間でも—平行線の取り扱いが異なることである[2]。これらの改革的な教科書に批判的な人物がいないはずはなく、そのうちの一人としてチャールズ・ドッジソン(ルイス・キャロルとして知られる)は戯曲 Euclid and His Modern Rivals(『ユークリッドと彼の現代のライバルたち』)を書き、それらテキストを扱き下ろした[3]
初期の改革的教科書の一つが、ジェームス・ウィルソン・モリス の1868年の著書 Elementary Geometry[4](「初等幾何学」)である。ウィルソンは自身の「方向」(direction) という原始概念に依拠した平行線の定義に基づいていた。ヴィルヘルム・キリングに従えば[5]、この考え方はライプニッツにまで遡れる[6]。ウィルソンは、原始概念として未定義のまま「方向」という言葉をほかの定義で用いており、例えば6番目の定義は「互いに交わる二つの直線はそれぞれ異なる方向を持ち、それら方向の差はそれらの間の「角」である」のように述べている[7]。定義 15 において平行線は以下のように導入される:「同じ向きを持つが一つの同じ直線の部分となっていない直線を平行線と呼ぶ」[8]。オーガスタス・ド・モルガンはこの教科書を批評して、主にこの定義およびウィルソンが平行線に関する内容を証明するのに用いた方法に基づいて誤りであると断じた。ドッジソンもまた、ウィルソンによる平行線の取り扱いを非難するために、彼の戯曲の大部分を当てている (Act II, Scene VI § 1)。ウィルソンは自身の教科書の第三版以降、これを改めている[9]。
他の改革者たちによって提案された、平行線の定義の置き換えとして用いられた他の性質も、大きく優れるものはなかった。主な難点は、ドッジソンの指摘したように、それらを用いるために系に余計な公理を追加する必要があったことである。ポセイドニウスの等距離直線としての定義は、Francis Cuthbertson が1874年の著書 Euclidean Geometry で解説したように、直線の片側に与えられた一定の距離に位置する点の全体が直線を成すことを示さなければならないという問題から逃れられない。これは証明できることではなく、それが真であるというのは改めて公理として要請しなければならないのである[10]。横断線による同位角の性質を用いた定義は W. D. Cooley が1860年の著書 The Elements of Geometry, simplified and explained で用いたが、この性質を利用するには「一つの直線が直線の対に横断的に交わるとき同位角が合同となるならば、任意の横断線においてもそうでなければならない」という主張の証明が求められ、その正当化にはやはり新たな公理が必要であった。
平面幾何[編集]
平行条件[編集]

ユークリッド空間内の互いに平行な直線 l, m に対し、以下の性質は互いに同値である:
- 互いに一様等距離: 直線 m 上の点は、直線 l との(最短)距離がどの点においても同一の値を持つ
- 直線 m は直線 l と同一平面上にあるが、l とは交わらない(ここで、直線とは何れの方向にも無限に伸びているものを言うことに注意)
- 二直線 m, l がともに同一平面上にある第三の直線(横断線)と交わるとき、それらが横断線との交わりで生じる同位角が互いに合同である。
これらの性質は互いに同値であるから、これらのうち任意の一つをユークリッド空間における平行線の定義として採用することができるが、最初と最後のものは長さや角度を測ったりする操作が含まれ、そのぶん真ん中の性質よりは複雑になっている。そこで、真ん中の性質をユークリッド空間における平行性の定義に採用するのが普通である[11]。そしてほかのふたつの性質は平行線の公理からの帰結ということになる。ほかにも、傾きを測る操作を含めれば、直線が互いに平行ということをそれらの傾きが同じであることによって定義することができる。
作図[編集]
上記の三性質からは三種類のそれぞれ異なる平行線の作図法が与えられる[注釈 2]
- 問題
- 点 a を通り、直線 l に平行な直線を引くこと

- 作図法
-
1: 直線 m は直線 l に対する距離が至る所同じ
-
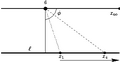
2: a を通る任意の直線が l と x において交わるとき、x を無限遠へ動かす
-
3: a を通る l, m に共通の横断線が、両者と直角に交わる
平行線の間の距離[編集]
ユークリッド平面内の平行線は等距離だから、平行な二直線間の距離は一意に決まる。軸に平行でない平行二直線の方程式を
同様に、直線を一般形の方程式
空間幾何[編集]
- 空間直線同士の場合
- 同一の三次元空間内にある二直線が互いに交わらないとき、それらは平行とは限らない。それらが平行となるのは、それらが同一平面上にある場合に限る。そうでないとき、それらはねじれの位置にある。
- 三次元空間内の相異なる直線 l, m が平行となるための必要十分条件は、m 上の点 P から測った l 上の最も近い点への距離が、P のとり方に依らないことである。これはねじれの位置にある場合には絶対に成り立たない。
- 直線と平面の場合
- 同じ三次元空間内にある直線 m と平面 q で、m が平面 q 上にないとき、それらが平行となる必要十分条件は、それらが交わらないことである。
- もちろん、それらが平行であるための必要十分条件を、m 上の任意の点 P から測った q 上の最も近い点への距離が P の位置のとり方に依らないことと述べることもできる。
- 平面同士の場合
- 「互いに平行となる必要十分条件がそれらが共有点を持たないことである」という同一平面上の平行線に対すると同様の事実が、同一三次元空間内の平行面に対しても成立する。
- また、同一三次元空間内の相異なる二つの平面 q, r が平行となる必要十分条件は、平面 q 上の点 P から平面 r 上の最も近い点へ測った距離が P の位置の選び方に依らないことである。このことは、より高次の空間内で考える場合には、同一三次元空間内にない二つの平面では成り立たない。
反射的な平行性[編集]
綜合的アフィン幾何学において、直線が互いに平行であるという関係は、ユークリッド幾何学における用法からやや修正した基本概念である。平行性が対称かつ推移的な関係であることは明らかであり、それが反射的ならば同値関係が定まる。ふつう、ユークリッド幾何学において直線は自分自身と平行とは考えないが、アフィン幾何学においては自分自身と平行(したがって同値関係を成す)と考える[12]:192[13]:17 のが便利である。
この種の平行関係を記述する別の方法は、交わりが一点でない交線も考えることである。すなわち、二つの直線が互いに平行とは、それらの全ての点が共通点であるか、さもなくば共有点が一つもないこととする。このことは、アフィン幾何学およびユークリッド幾何学で用いられるプレイフェアの公理では、平行関係が平面上の直線全体の成す集合上の推移的関係を成すという主張に同値であるとの注意がある[14]:372
非ユークリッド幾何における平行性[編集]
非ユークリッド幾何学においては、直線の代わりに測地線に対して述べるのがより一般的で、測地線の意味で「直線」の語がしばしば用いられる。測地線とはすなわち与えられた幾何における二点間の最短経路を意味する。楕円幾何や双曲幾何では、上で述べた三性質は互いに同値ではなく、特に長さや角度を測る操作を含まないものだけが非ユークリッド幾何においても有効である。三性質は、このような一般の幾何においては、それぞれ等距離を保つ曲線 (equidistant curves), 互いに平行な測地線 (parallel geodesics), 共通垂線を持つ測地線 (geodesics sharing a common perpendicular) という異なる種類の関係を定める。
双曲幾何[編集]
ユークリッド幾何学において二つの測地線(直線)は交わるか平行の二択しかないが、双曲幾何学では選択肢は三つある。すなわち、同一平面上にある二つの測地線は:
- 交わる: その平面内の一つの共有点でそれらは交わる;
- 平行: 平面内では交点を持たないが、共通の無限遠点に収束する(無限遠点で交わる);
- 超平行: 極限において共通の無限遠点を持たない
文献によっては「超平行」(ultra parallel) な測地線は「交わらない」という言い方もしばしば用いられる。「無限遠点で交わる」測地線は漸近的平行線ともいう。
直線 l 上にない点 a を通る漸近的平行線は二つ存在し、それぞれ l の各方向における理想点(無限遠点)に対応している。この二つの直線は、l に交わる直線と、l に超平行な直線とを隔てる境界線になっている。
超平行線は共通垂線をただ一つ持ち(超平行定理)、この共通垂線の両側で発散する。
楕円幾何[編集]
球面幾何における測地線は大円であり、大円は球面を二つの等しい半球面に分割、またどの二つの大円も互いに交わる。したがって、与えられた測地線に平行は測地線は存在せず、すべて交わる測地線に分類される。球面上の互いに距離を保つ曲線を平行緯線 (parallels of latitude) と呼ぶ。互いに平行な緯線は、球面の中心を通る平面に平行な平面とその球面との交わりによって生成される。
関連項目[編集]
注[編集]
注釈[編集]
- ^ 平行線公準は直線が互いに交わる場合のみ言及しているけれども、それはプレイフェアの公理の意味での平行線の一意性を示すことが必要な内容である
- ^ 三番目のみが定木とコンパスを用いた作図であり、前二つは「無限回の手順」を要する無限作図になる
出典[編集]
- ^ a b Heath 1956, pp. 190–194.
- ^ Richards 1988, pp. 161–200, Chap. 4: Euclid and the English Schoolchild..
- ^ Carroll, Lewis (2009) [1879], Euclid and His Modern Rivals, Barnes & Noble, ISBN 978-1-4351-2348-9
- ^ Wilson 1868.
- ^ Einführung in die Grundlagen der Geometrie, I, p. 5
- ^ Heath 1956, p. 194.
- ^ Wilson 1868, p. 2.
- ^ Wilson 1868, p. 12.
- ^ Richards 1988, pp. 180–184.
- ^ Heath 1956.
- ^ Wylie, Jr. 1964, pp. 92–94.
- ^ Coxeter, H. S. M. (1961), Introduction to Geometry, John Wiley & Sons
- ^ Szmielew, Wanda (1983), From Affine to Euclidean Geometry, D. Reidel, ISBN 90-277-1243-3
- ^ Liu, Andy (2011), “Is parallelism an equivalence relation?”, The College Mathematics Journal 42 (5)
参考文献[編集]
- Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications
- (3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text.
- Richards, Joan L. (1988), Mathematical Visions: The Pursuit of Geometry in Victorian England, Boston: Academic Press, ISBN 0-12-587445-6
- Wilson, James Maurice (1868), Elementary Geometry (1st ed.), London: Macmillan and Co.
- Wylie, Jr., C.R. (1964), Foundations of Geometry, McGraw–Hill
関連文献[編集]
- Papadopoulos, Athanase; Théret, Guillaume (2014), La théorie des parallèles de Johann Heinrich Lambert : Présentation, traduction et commentaires, Paris: Collection Sciences dans l'histoire, Librairie Albert Blanchard, ISBN 978-2-85367-266-5
外部リンク[編集]
- Weisstein, Eric W. "Parallel". mathworld.wolfram.com (英語).
- Definition:Parallel at ProofWiki
- parallel lines in hyperbolic geometry - PlanetMath.(英語)
- parallelism of line and plane - PlanetMath.(英語)
- compass and straightedge construction of parallel line - PlanetMath.(英語)
- BSE-3 (2001), “Parallel straight lines”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Ivanov, A.B. (2001), “Anti-parallel straight lines”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Sabitov, I.Kh. (2001), “Parallel surfaces”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4