群準同型
| 代数的構造 → 群論 群論 |
|---|
 |
数学、特に群論における群の準同型写像(じゅんどうけいしゃぞう、英: group homomorphism)は群の構造を保つ写像である。準同型写像を単に準同型とも呼ぶ。
定義と注意[編集]
ふたつの群 (G, ∗) と (H, ⋅) が与えられたとする。(G, ∗) から (H, ⋅) への群準同型とは、写像 h: G → H で、
定義から、準同型写像 h は、G の単位元 eG を H の単位元 eH に写し、また
- 注意
- 古い記法では、h(x) は xh や xh と表記されていた。ただしこの記法では、何らかの指数や一般の添字などと混同しやすい。なお、より最近の記法では準同型を引数の右側から作用させるときは括弧を書かないというようなものもある。この場合 h(x) は単に xh と書ける。これは特に、オートマトンによる機械処理を行う分野で一般的である。オートマトンは左から右へ順番に読めばいいので処理しやすいためである。
群に何か別の構造が付加されている場合には、「準同型」という言葉は(上記のような)群構造だけではなくて、付加された構造についてもよく振舞うをこと意味していることもある。たとえば、位相群の準同型といえば、しばしば連続性も要求される。
群 G から H への群準同型全体のなす集合は Hom(G, H) と表記される。
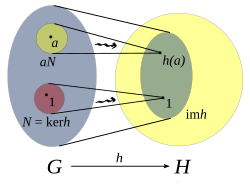
像と核[編集]
準同型 h: G → H の核 ker(h) を、h によって H の単位元にうつる G の元全体の集合
準同型の核と像は、その準同型がどのくらい同型に近いかを測るものと解釈することができる。第一同型定理によれば、準同型 h: G → H の像 im h は、余像と呼ばれる商群 G/ker h に同型である。
例[編集]
- 巡回群 Z/3Z = {0, 1, 2} と、整数全体の成す加法群 Z を考える。 h(u) ≔ u mod 3 によって定義される写像 h: Z → Z/3Z は群準同型である。これは全射であり、核は3の倍数全体の成す集合である。
- 指数関数は、実数全体の成す加法群 R から、非零実数全体の成す乗法群 R* への準同型 exp: R → R* を与える。核は {0} であり、像は正の実数全体 R+ である。
- 指数関数はまた、複素数全体の成す加法群 C から、非零複素数全体の成す乗法群 C* への準同型をも与える。この写像は全射であり、核はオイラーの公式から明らかなように { 2πki | k ∈ Z } となる。R や C のように、その加法群から乗法群への準同型を持つ体を指数体と言う。
- 有限集合 {1, …, n} 上の置換 σ に対して符号 sgn(σ) を対応させる写像 sgn: Sn → {±1} は群準同型である。ここで Sn は n 次対称群である。この群準同型は n > 1 のとき全射であり、その核は n 次交代群 An と呼ばれる。
- 複素成分の n 次正則行列 A に対して行列式 det(A) を対応させる写像 det: GLn(C) → C* は群準同型である。ここで GLn(C) は複素数体上の n 次一般線型群である。この群準同型は全射であり、その核は n 次特殊線型群 SLn(C) と呼ばれる。
- 実成分の n 次正則行列 A に対して逆行列の転置 θ(A) = tA−1 を対応させる写像 θ: GLn(R) →GLn(R) は群(準)同型である。このとき θ で固定される行列の全体 { A | θ(A) = A } は直交群 O(n) となる。
- 零でない複素数 z = reiθ に対して絶対値 |z| = r を対応させる写像 C* → R* は群準同型である。この写像の像は正の実数の全体 { r | r > 0 } であり、核は複素平面の単位円に属する複素数の全体 { eiθ | 0 ≤ θ < 2π } である。
- 奇素数 p についてルジャンドル記号は (Z/pZ)* = {1, …, p − 1} から {±1} への群準同型 a ↦ ap − 1/2 mod p を定める。
群の圏[編集]
h: G → H および k: H → K が群準同型ならば、それらの合成 k ∘ h: G → K もまた群準同型である。これにより、群全体の成す(圏論的な意味での)類に群準同型を射としてあわせて考えたものは、群の圏 Grp と呼ばれる圏を成す。
準同型写像の種類[編集]
準同型 h: G → H が全単射ならば、その逆写像もまた準同型になることが示せる。このとき h は群同型写像 (group isomorphism) であるといい、群 G と H は互いに同型 (isomorphic) であるという。互いに同型な群というのは、その元の記述の仕方が違うだけで、実用上は同一視できる。
定義域と終域が同じ群準同型写像 h: G → G は G の自己準同型写像という。さらに、h が全単射、すなわち同型になるとき、自己同型という。G のすべての自己同型からなる集合は、写像の合成を演算として群をなす。これを、G の自己同型群と言い、Aut(G) と表記する。たとえば、群 (Z, +) の自己同型群は、恒等変換と −1 倍写像の二つの元のみからなり、Z/2Z に同型である。
全射準同型(つまり、上への写像となっているような準同型)を全準同型 (epimorphism) という。また、単射準同型(つまり、一対一写像となっていうような準同型)を単準同型 (monomorphism) という。
アーベル群の準同型[編集]
G と H をアーベル群(つまり、演算が可換な群)とすると、G から H への群準同型全体の成す集合 Hom(G, H) をそれ自身ひとつのアーベル群とすることができる。ただし準同型 h と k の和 h + k を点ごとの和、すなわち
準同型の加法は、準同型の合成と以下の意味で両立する:
- Hom(K, G) の任意の元 f および Hom(G, H) の任意の元 h, k および Hom(H, L) の任意の元 g に対して およびが成り立つ。
これはアーベル群 G の自己準同型全体の成す集合 End(G) は(準同型の和と合成に関して)環を成すことを示している。環 End(G) をアーベル群 G の自己準同型環 と言う。たとえば、巡回群 Z/nZ の m 個の直和として得られるアーベル群 G の自己準同型環 End(G) は Z/nZ に成分を持つ m-次正方行列全体の成す環に同型である。上記の和と合成に関する両立性はアーベル群(と群準同型)の圏 Ab が前加法圏を成すことをも示している。直和の存在や核がよく振舞うことから、圏 Ab はアーベル圏の原型的な例となっている。
関連項目[編集]
参考資料[編集]
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, MR1878556, ISBN 978-0-387-95385-4
外部リンク[編集]
- Weisstein, Eric W. "Group Homomorphism". mathworld.wolfram.com (英語).
- group homomorphism in nLab
- group homomorphism - PlanetMath.(英語)
- Group Homomorphism at ProofWiki
- Hazewinkel, Michiel, ed. (2001), “Homomorphism”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4









