サポートベクターマシン

サポートベクターマシン（英: support vector machine, SVM）は、教師あり学習を用いるパターン認識モデルの一つである。分類や回帰へ適用できる。1963年に Vladimir N. Vapnik, Alexey Ya. Chervonenkis が線形サポートベクターマシンを発表し、1992年に Bernhard E. Boser, Isabelle M. Guyon, Vladimir N. Vapnik が非線形へと拡張した。

サポートベクターマシンは、現在知られている手法の中でも認識性能が優れた学習モデルの一つである。サポートベクターマシンが優れた認識性能を発揮することができる理由は、未学習データに対して高い識別性能を得るための工夫があるためである。

基本的な考え方

サポートベクターマシンは、線形入力素子を利用して 2 クラスのパターン識別器を構成する手法である。訓練サンプルから、各データ点との距離が最大となるマージン最大化超平面を求めるという基準（超平面分離定理）で線形入力素子のパラメータを学習する。

最も簡単な場合である、与えられたデータを線形に分離することが可能な（例えば、3次元のデータを2次元平面で完全に区切ることができる）場合を考えよう。

このとき、SVMは与えられた学習用サンプルを、もっとも大胆に区切る境目を学習する。 学習の結果得られた超平面は、境界に最も近いサンプルとの距離（マージン）が最大となるパーセプトロン（マージン識別器）で定義される。 すなわち、そのようなパーセプトロンの重みベクトル ${\boldsymbol {w}}\in \mathbb {R} ^{p}$ を用いて、超平面は $\{{\boldsymbol {x}}\in \mathbb {R} ^{p}\mid {\boldsymbol {x}}\cdot {\boldsymbol {w}}=0\}$ で表される。

学習過程はラグランジュの未定乗数法とKKT条件を用いることにより、最適化問題の一種である凸二次計画問題で定式化される。 ただし、学習サンプル数が増えると急速に計算量が増大するため、分割統治法の考え方を用いた手法なども提案されている。

概念的特長

次のような学習データ集合 ${\mathcal {D}}$ が与えられた場合を考える。

${\mathcal {D}}=\{({\boldsymbol {x}}_{i},y_{i})\mid {\boldsymbol {x}}_{i}\in \mathbb {R} ^{p},\,y_{i}\in \{-1,1\}\}_{i=1}^{n}$

$y_{i}$ は 1 もしくは -1 の値を持つ変数で ${\boldsymbol {x}}_{i}$ が属したクラスを意味する。 ${\boldsymbol {x}}_{i}$ は $p$ 次元の特徴ベクトルである。

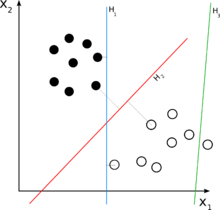
H3 は二つのクラスのいくつかの点を正しく分類していない。H1 と H2 は二つのクラスのいくつかの点を分類するのに、H2 が H1 よりもっと大きいマージンを持って分類することを確認することができる。

ニューラルネットワークを含む多くの学習アルゴリズムは、このような学習データが与えられた時 $y_{i}=1$ であるいくつかの点と $y_{i}=-1$ であるいくつかの点とを分離する超平面をさがすのが共通の目標であるが、SVMが他のアルゴリズムと差別化される特徴はただいくつかの点を分離する超平面を捜すことで終わるのではなく、いくつかの点を分離することができる幾多の候補平面の中でマージンが最大になる超平面 (maximum-margin hyperplane) を探す点にある。ここでマージンとは、超平面から各いくつかの点に至る距離の最小値を言い、このマージンを最大にしながらいくつかの点を二つのクラスで分類しようとすると、結局クラス 1 に属するいくつかの点との距離の中の最小値とクラス -1 に属するいくつかの点との距離の中の最小値とが等しくなるように超平面が位置しなければならず、このような超平面をマージン最大の超平面という。結論として、SVMは二つのクラスに属しているいくつかの点を分類する幾多の超平面の中で、最大限に二つのクラスのいくつかの点と距離を維持するものを探すアルゴリズムといえる。

線形分離不可能な問題への適用

1963年にウラジミール・ヴァプニク, Alexey Ya. Chervonenkis が発表した初期のサポートベクターマシンは、線形分類器にしか適用できなかった。 しかし、再生核ヒルベルト空間の理論を取り入れたカーネル関数を用いてパターンを有限もしくは無限次元の特徴空間へ写像し、特徴空間上で線形分離を行う手法が 1992年に Bernhard E. Boser, Isabelle M. Guyon, Vladimir N. Vapnik らによって提案された。 これにより、非線形分類問題にも優れた性能を発揮することがわかり、近年特に注目を集めている。

なお、カーネル関数を取り入れた一連の手法では、どのような写像が行われるか知らずに計算できることから、カーネルトリック (Kernel Trick) と呼ばれている。

主に下記のカーネル関数がよく使われていて LIBSVM でも実装されている。

• 線形
• 多項式
• 放射基底関数
• シグモイド関数

構造化SVM

2005年に Ioannis Tsochantaridis らが構造化SVM（英: structured SVM）を発表した。任意のデータ構造を扱えるように拡張したものである。

通常の二値分類SVMは以下の値で分類する。

${\hat {y}}(x;w)={\text{sign}}\langle w,x\rangle$

これは、このようにも書ける。

${\hat {y}}(x;w)={\underset {y\in \{-1,1\}}{\operatorname {arg\,max} }}\ \langle w,yx\rangle$

その上で、これを二値から一般の値に拡張する。$\Psi$ は入出力から特徴量を作り出す実数ベクトルを返す関数。問題ごとに定義する。

${\hat {y}}(x;w)={\underset {y\in {\mathcal {Y}}}{\operatorname {arg\,max} }}\ \langle w,\Psi (x,y)\rangle$

そして、下記の損失関数を最小化するように、最適化問題を解く。ここではL2正則化を付けている。$C$ は正則化の強さを表す定数。$\Delta$ は出力の類似度を表す実数を返す関数。問題ごとに定義する。$\Delta (y,y)=0$ であり、異なる値同士なら 0 よりも大きくなるように設計する。

$E(w)=\|w\|^{2}+C\sum _{i=1}^{n}\Delta (y_{i},{\hat {y}}(x_{i};w))$

上記の最適化問題を解くには工夫が必要であり、その後も提案が続いているが、2005年に提案された方法は下記のように上界となる関数 $L_{i}(w)$ を作る。

$\Delta (y_{i},{\hat {y}}(x_{i};w))\leq L_{i}(w)$

その上で、下記の最適化問題を解く。

$E(w)=\|w\|^{2}+C\sum _{i=1}^{n}L_{i}(w)$

$L_{i}(w)$ の作り方として2通りが提案された。

マージン リスケーリング

$L_{i}(w)=\sup _{y\in {\mathcal {Y}}}\Delta (y_{i},y)+\langle w,\Psi (x_{i},y)\rangle -\langle w,\Psi (x_{i},y_{i})\rangle$

スラック リスケーリング

$L_{i}(w)=\sup _{y\in {\mathcal {Y}}}\Delta (y_{i},y)\left(1+\langle w,\Psi (x_{i},y)\rangle -\langle w,\Psi (x_{i},y_{i})\rangle \right)$

関連項目

• カーネル法
• 逐次最小問題最適化法 (SMO)
• 人工知能
• パターン認識
• 放射基底関数
• 線形分類器
• 実装
  • LIBSVM（一般）、LIBLINEAR（線形）
  • scikit-learn（LIBSVM, LIBLINEARのPythonラッパーを含む）