軌道力学
| 宇宙力学 |
|---|
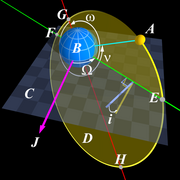 |
軌道力学(きどうりきがく)は、弾道学と天体力学の応用で、ロケットや宇宙船の軌道に関する現実的な問題を解決するための学問である。これらの物体の軌道は、ニュートン力学と万有引力から計算することができる。軌道力学は、宇宙探査ミッションの設計や制御の基本原理である。天体力学は、重力の下での、軌道力学よりも広範な領域を扱い、宇宙船も恒星系、惑星、衛星、彗星等を含めた天体も、どちらも対象となる。軌道力学は、軌道マヌーバ、軌道平面の変更、惑星間移動も含めた宇宙船の軌道に対象を絞っており、ミッションの計画者が宇宙機の推進を予測するために用いられる。一般相対性理論は、ニュートンの法則より正確に軌道を計算し、高い精確さが必要な場面や太陽近傍等の重力が非常に強い環境では必須である。
歴史[編集]
20世紀に宇宙飛行が実現するまで、軌道力学と天体力学の間には、ほとんど差異がなかった。時間の関数として位置を決定するケプラーの問題を解くために用いるような基本技術は、どちらの学問領域でも同じだった。さらに、この学問分野の歴史はほぼ共有していた。
ヨハネス・ケプラーは、高い正確性で惑星の軌道のモデル化に成功した最初の人物であり、1605年にケプラーの法則を発表した。アイザック・ニュートンは、天体の運動のより一般的な法則を1687年の著書『自然哲学の数学的諸原理』の中で発表した。
実用的な技術[編集]
経験則[編集]
以下の経験則は、標準的な前提の下で天体力学で近似できる状況にとって有用である。議論されている特定の例は、惑星の周囲を公転する衛星であるが、この経験則は恒星の周囲の小天体のような他の状況にも適用することができる。
- ニュートンの法則から数学的に導くことができるケプラーの法則は、非重力的な力がなく重力を及ぼし合っている2つの天体か、太陽のような巨大質量の天体による重力が他の力に卓越していると近似できる場合にのみ精確である。
- 軌道は楕円形で、楕円の焦点の1つに重い天体がくる。この特別な場合が、惑星が中心に来る円形軌道(円は、離心率が0の楕円である)と惑星が焦点に来る放物線軌道(離心率がちょうど1で、無限に長い楕円とみなせる)である。
- 惑星から衛星に引いた直線は、軌道上の位置に関わらず、同じ時間に同じ面積を掃く。
- 衛星の軌道周期の2乗は、惑星からの平均距離の3乗に比例する。
- 推力がなければ、衛星の軌道の高さと形は変化せず、不動の恒星に対して同じ角度を保つ。
- 低軌道(または楕円軌道の近点付近)の衛星は、重力がより強く作用するため、惑星の表面に対して、高軌道(または楕円軌道の遠点付近)の衛星よりも速く運動する。
- 衛星の軌道上の一点で推力が働いた場合、その衛星は、軌道上の同じ点に戻ってくる。そのため、1つの円軌道から別の軌道に遷移させる場合には、少なくとも2度推力を働かせる必要がある。
- 円軌道において、衛星の速度を遅くする方向に推力を働かせると、その点から180度の地点に近点を持つ楕円軌道となる。衛星の速度を速くする方向に推力を働かせると、その点から180度の地点に遠点を持つ楕円軌道となる。
軌道力学の法則の結果は、時として直観と相容れないことがある。例えば、同じ円軌道上の2機の宇宙船がドッキングしようとする場合、その位置が非常に接近していない時に、後ろの宇宙船は速度を速めるために単純にエンジンを吹かすことはできない。そうすると軌道の形が変化し、ターゲットと出会うことができない。ドッキングするための1つの方法は、速度を下げるために逆向きにエンジンの噴射を行い、その後、低い円軌道に戻すために再度噴射を行う。低軌道は高軌道よりも速度が速いため、後ろの宇宙船は追いつくことが出来る。3度目の噴射で、先行する宇宙船の軌道と交わり、後ろから接近できるような楕円の軌道に移行する。
標準的な前提が適用できないようなレベルであれば、実際の軌道は計算したものからずれることになる。例えば、大気の抗力は、地球軌道にある物体について複雑化要因になり得る。これらの経験則は、連星系等の同程度の質量の2つかそれ以上の物体に適用する際には、不正確になる。惑星のような大きな物体にとっては、古典力学と一般相対性理論の差異も重要になる。
天体力学の法則[編集]
天体力学の基本法則は、ニュートンの万有引力の法則とニュートンの運動の法則であり、ニュートンの開発した微分積分学がその計算のための重要な数学的ツールになる。
ケプラーの法則は、周回する天体が中心の天体からの重力のみを受けていると見なせる場合には、ニュートンの法則から導くことができる。推力が働く場合、ニュートンの法則は適用できるが、ケプラーの法則は成り立たなくなる。推力が止まると、結果として軌道は変わるが、再びケプラーの法則が適用できるようになる。ケプラーの3法則は、次のとおりである。
- 全ての惑星の軌道は、太陽を1つの焦点とした楕円である。
- 惑星と太陽を結ぶ直線は、等しい時間で等しい面積を掃く。
- 惑星の軌道周期の2乗は、軌道長半径の3乗と比例する。
脱出速度[編集]
脱出速度の公式は、以下のように簡単に導くことができる。全ての宇宙船の単位質量当たりのエネルギーは、単位質量当たりの位置エネルギーと単位質量当たりの運動エネルギーという2つの成分から成り立っている。単位質量当たりの位置エネルギーは、惑星の質量Mと関係があり、次の式で与えられる。
一方、単位質量当たりの運動エネルギーは、次の式で与えられる。
エネルギー保存の法則から、単位質量当たりの合計の軌道エネルギー
は、中心の天体から宇宙船までの距離には依存しない。これより、天体は、この値が負ではない時に無限大に達し、これは、以下を意味する。
地球表面からの脱出速度は、約11km/sであるが、太陽の重力があるため、物体を無限の距離まで送るにはこの速度では不十分である。地球から太陽までの距離で地球の近傍以外の場所から太陽系の外への脱出速度は、約42km/sであるが、地球から打ち上げられる宇宙船は、方向が同じであれば地球の公転速度も利用することができる。
自由軌道の公式[編集]
軌道は円錐曲線であるため、所与の角度の天体までの距離の公式は、極座標系での曲線の公式と一致し、次のようになる。
ここで、μは標準重力パラメータ、Gは重力定数、m1とm2は天体1と天体2の質量、hは天体1に対する天体2質量当たりの角モーメントである。パラメータθは、真近点角、pは半通径、eは軌道離心率として知られる値であり、全て6つの軌道要素から導くことができる。
円軌道[編集]
中心の天体の重力が独占的な全ての軌道は、楕円軌道となる。この特殊なケースは円軌道であり、これは軌道離心率が0の楕円軌道である。質量Mの重力中心からの距離rにおける円軌道上の天体の速度は、次の公式で表される。
ここで、は重力定数であり、次の値と等しい。
- 6.672 598 × 10−11 m3/(kg・s2)
この公式を適切に使うためには、単位は一貫していなければならず、例えばMはkg、rはmで表されていなければならない。答えはm/sの単位で得られる。
GMの大きさは、しばしば標準重力パラメータと呼ばれ、太陽系のそれぞれの惑星や衛星で異なった値である。
円軌道の速度が既知になると、2の平方根をかけることで簡単に脱出速度が求められる。
楕円軌道[編集]
軌道離心率が0<e<1であれば、自由軌道の方程式の分母が真近点角θに伴って変化するが、0になることはなく、必ず正の値である。そのため、相対的な位置ベクトルは有界であり、近点rpにおける最小値は、以下の式で与えられる。
最大値rは、θ=180°の時である。この点は遠点と呼ばれ、raで示される動径座標は、次のようになる。
近点Pから遠点Aまでの距離を2aとすると、以下の方程式が成り立つ。
上記の方程式を展開して、次の値が得られる。
aは、楕円軌道の軌道長半径である。rについて解くと、次のようになる。
軌道周期[編集]
標準的な前提の下で、楕円軌道を公転する物体の軌道周期 () は、次のように計算される。
ここで、
- は標準重力パラメータで、
- は軌道長半径の長さである。
ここから次の結論が得られる。
- 軌道周期は、軌道長半径の長さ () が等しい円軌道の周期と同じである。
- 所与の軌道長半径に対し、軌道周期は軌道離心率に依存しない(ケプラーの第3法則)。
速度[編集]
標準的な前提の下で、楕円軌道を公転する物体の軌道速度()は次のように計算される。
ここで、
- は標準重力パラメータ、
- は天体間の距離、
- は軌道長半径の長さである。
双曲線軌道の速度の方程式は、+ となるか、aが負の場合は上式となる。
エネルギー[編集]
標準的な前提の下で、楕円軌道を公転する物体の質量当たりの軌道エネルギー()は負となり、この軌道の軌道エネルギー保存の方程式は、次のような形になる。
ここで、
- は周回する天体の軌道速度、
- は中心の天体から周回する天体までの距離、
- は軌道長半径の長さ、
- は標準重力パラメータである。
ここから次の結論が得られる。
- 所与の軌道長半径では、質量当たりの軌道エネルギーは軌道離心率に依存しない。
ビリアル定理を用いると、次のことが分かる。
- 質量当たりの位置エネルギーの時間平均は、2εに等しい。
- r?1の時間平均は、a?1である。
- 質量当たりの位置エネルギーの時間平均は、-εに等しい。
放物線軌道[編集]
軌道離心率が1と等しい場合、軌道の方程式は次のようになる。
ここで、
- は中心の天体から周回する天体までの距離、
- は周回する天体の質量当たりの角モーメント、
- は周回する天体の真近点角、
- は標準重力パラメータである。
真近点角θが180°に近づくと、分母は0に近づき、rは無限大に発散する。従って、e=1の時の軌道エネルギーは0であり、次の式で表される。
ここで、
- は周回する天体の軌道速度である。
言い換えると、放物線軌道上の任意の点の速度は、次のようになる。
双曲線軌道[編集]
軌道離心率がe>1であれば、双曲線軌道となり、軌道方程式は次のようになる。
この系は2つの対称な曲線で構成されている。周回する天体がそのうちの1つを占め、もう1つはその空の数学的な像になる。明らかに、上記の方程式の分母は、cosθ = -1/eとなると0になり、この時の真近点角の値を次のように示す。
θ∞ = cos-1(-1/e)
真近点角がθ∞に近づくと、半径方向距離が無限大になる。θ∞は、「漸近線の真近点角」として知られる。θ∞を90°から180°の間とすると、sin2θ+cos2θ=1という三角関数の性質から、次のように書ける。
sinθ∞ = (e2-1)1/2/e
エネルギー[編集]
標準的な前提の下で、双曲線軌道の質量当たりの軌道エネルギー()は0より大きく、軌道エネルギー保存の法則により、次の式が成り立つ。
ここで、
- は周回する天体の起動速度、
- は中心の天体から周回する天体までの距離、
- は負の軌道長半径、
- は標準重力パラメータである。
双曲線過剰速度[編集]
標準的な前提の下で、双曲線軌道を公転する天体は、無限遠点で双曲線過剰速度()と呼ばれる軌道速度に到達する。この速度は、以下の式で表される。
ここで、
- は標準重力パラメータ、
- は双曲線軌道の負の軌道長半径である。
双曲線過剰速度は、質量当たりの軌道エネルギーに関係がある。
軌道の計算[編集]
ケプラーの方程式[編集]
主に歴史的に使われてきた軌道を計算する方法の1つは、ケプラーの方程式である。
- .
ここで、Mは平均近点角、Eは離心近点角、は軌道離心率である。
ケプラーの公式では、近点から真近点角に至るまでの時間は、2つのステップによって求められる。
- 真近点角から離心近点角を求める。
- 離心近点角から時間を求める。
逆に与えられた時間の離心近点角を求めるのはより難しい。ケプラーの方程式はに対して超越的で、つまりについて代数的に解くことはできない。ただし、反転させて解析関数的に解くことはできる。
全ての実数に対して適用できるケプラーの方程式の解は、以下のとおりである。
この値を求めることで、次の式が出る。
脚注[編集]
- Curtis, Howard D., (2009). Orbital Mechanics for Engineering Students, 2e. New York: Elsevier. ISBN 978-0-12-374778-5
- Bate, Roger R.; Mueller, Donald D., and White, Jerry E. (1971). Fundamentals of Astrodynamics. New York: Dover Publications. ISBN 0-486-60061-0
- Sellers, Jerry J.; Astore, William J., Giffen, Robert B., Larson, Wiley J. (2004). Kirkpatrick, Douglas H.. ed. Understanding Space: An Introduction to Astronautics (2 ed.). McGraw Hill. pp. 228. ISBN 0-07-242468-0
- “Air University Space Primer, Chapter 8 - Orbital Mechanics”. USAF. 2012年9月20日閲覧。
参考文献[編集]
- Bate, R.R., Mueller, D.D., White, J.E., (1971). Fundamentals of Astrodynamics. Dover Publications, New York. ISBN 978-0-486-60061-1
- Vallado, D. A. (2001). Fundamentals of Astrodynamics and Applications, 2nd Edition. Springer. ISBN 978-0-7923-6903-5
- Battin, R.H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics. American Institute of Aeronautics & Ast, Washington, D.C.. ISBN 978-1-56347-342-5
- Chobotov, V.A. (ed.) (2002). Orbital Mechanics, 3rd Edition. American Institute of Aeronautics & Ast, Washington, D.C.. ISBN 978-1-56347-537-5
- Herrick, S. (1971). Astrodynamics: Orbit Determination, Space Navigation, Celestial Mechanics, Volume 1. Van Nostrand Reinhold, London. ISBN 978-0-442-03370-5
- Herrick, S. (1972). Astrodynamics: Orbit Correction, Perturbation Theory, Integration, Volume 2. Van Nostrand Reinhold, London. ISBN 978-0-442-03371-2
- Kaplan, M.H. (1976). Modern Spacecraft Dynamics and Controls. Wiley, New York. ISBN 978-0-471-45703-9
- Tom Logsdon (1997). Orbital Mechanics. Wiley-Interscience, New York. ISBN 978-0-471-14636-0
- John E. Prussing and Bruce A. Conway (1993). Orbital Mechanics. Oxford University Press, New York. ISBN 978-0-19-507834-3
- M.J. Sidi (2000). Spacecraft Dynamics and Control. Cambridge University Press, New York. ISBN 978-0-521-78780-2
- W.E. Wiesel (1996). Spaceflight Dynamics, 2nd edition. McGraw-Hill, New York. ISBN 978-0-07-070110-6
- J.P. Vinti (1998). Orbital and Celestial Mechanics. American Institute of Aeronautics & Ast, Reston, Virginia. ISBN 978-1-56347-256-5
- P. Gurfil (2006). Modern Astrodynamics. Butterworth-Heinemann. ISBN 978-0-12-373562-1
関連項目[編集]
外部リンク[編集]
- ORBITAL MECHANICS (Rocket and Space Technology)
- Java Astrodynamics Toolkit















































![{\displaystyle E={\begin{cases}\displaystyle \sum _{n=1}^{\infty }{\frac {M^{\frac {n}{3}}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left({\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}^{n}\right)\right),&\epsilon =1\\\displaystyle \sum _{n=1}^{\infty }{\frac {M^{n}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left({\frac {\theta }{\theta -\epsilon \cdot \sin(\theta )}}^{n}\right)\right),&\epsilon \neq 1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/431f6158a62d71404b473fa462301971485c4fdb)
