漸近線

$グラフ y = x + .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/x$ の漸近線は $y$ 軸と直線 $y = x$ である。

解析幾何学において、平面曲線の漸近線（ぜんきんせん、英: asymptote）とは、十分遠くで曲線との距離が $0$ に近づき、かつ曲線と接しない直線のことである。通常の定義では、漸近線は曲線と無限回交わってもよい^[1]。

漸近線は存在するとは限らず、また複数存在する場合もある。漸近線は、曲線上の点が十分進んだ所での概形である。

特に、座標平面における関数に対しては、そのグラフの漸近線の方程式は（存在の可否も含めて）求め方が確立されている。関数のグラフの接線の極限が存在するならばそれは漸近線に等しい^[2]。

代数幾何学などでは、漸近線は無限遠点のみで曲線と接する直線と定義される^[3]^[4]。

漸近線として直線だけでなく曲線を考えることもある。

例[編集]

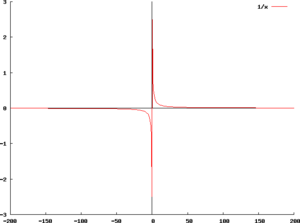
定数関数、多項式関数のグラフには、漸近線は存在しない。漸近線が存在する最も簡単な例は、関数 $f (x) = 1 / x$ のグラフである。このグラフの漸近線は、直線 $x = 0$ と直線 $y = 0$ である。グラフを描くと、曲線 $y = 1 / x$ は $x \to 0\pm$ , $x \to \pm\infty$ のときにそれぞれ $y$ 軸、 $x$ 軸に近づくことが見てとれる。この場合はグラフと漸近線は共有点を全く持たないが、一般にはそうとは限らない。漸近線が存在する関数は他にもいくつかある。

なかでも代表的なものは以下の通りである。

座標平面上の関数とその漸近線
関数名	関数式	漸近線の方程式
正接関数	$y = tan x$	$x = π / 2 + n π$ （ $n$ は整数）
指数関数	$y = a x (a > 0, a \neq 1)$	$y = 0$
対数関数	$y = log a x (a > 0, a \neq 1)$	$x = 0$
双曲線	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=\pm 1$ $(a > 0, b > 0)$	$y = \pm b / a x$
双曲線正接関数	$y=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$y = \pm1$
逆正接関数	$y = arctan x$	$y = \pm π / 2$
逆双曲線正接関数	$y = tanh -1 x = 1 / 2 log 1 + x / 1 - x$	$x = \pm1$

分数関数においては、分母が $0$ になるところで漸近線になり、 $x \to \pm\infty$ で漸近線が存在する場合があるが、それぞれ存在しないこともある。

どちらも存在しない例：

y={\frac {x^{4}+x^{2}+1}{x^{2}+1}}

無理関数で漸近線が存在するのは

y=\textstyle \sum \limits _{i=1}^{n}k_{i}{\sqrt[{p_{i}}]{(x-u_{i})^{p_{i}}\pm {a_{i}}^{p_{i}}}}+(bx+c)

(a i > 0)

の形に限られる（漸近線は $y=\textstyle \sum \limits _{i=1}^{n}k_{i}(x-u_{i})+bx+c$ ）。

グラフと漸近線がどんな遠くでも無限回交わる例もある。減衰曲線（ $y = sin x / x$ や $y = e - x sin x$ など）と $x$ 軸はその一例である。

関数の漸近線[編集]

関数 $y = f (x)$ のグラフの（直線である）漸近線は、次の2タイプである。

$y$ 軸に平行の直線（方程式を $x = a$ とする）
$x \to \infty$ または $x \to -\infty$ で漸近する直線（方程式を $y = ax + b$ とする）

$y$ 軸平行の漸近線[編集]

直線 $x = a$ がグラフ $y = f (x)$ の漸近線であるための必要十分条件は、以下の4つのいずれかを満たすことである。

$\lim _{x\to a+}f(x)=\infty ,$
$\lim _{x\to a+}f(x)=-\infty ,$
$\lim _{x\to a-}f(x)=\infty ,$
$\lim _{x\to a-}f(x)=-\infty .$

いずれも $x = a$ で不連続の場合である。したがって、関数の不連続点が、 $y$ 軸平行の漸近線の場所の候補である。

$x \to \pm\infty$ で漸近する直線[編集]

直線 $y = ax + b$ が $x \to \infty$ でグラフ $y = f (x)$ に漸近するとする（ $x \to -\infty$ の場合も同様）。このとき、 $a$ , $b$ は（存在の可否も含めて）次の極限で求められる。

$a=\lim _{x\to \infty }{\frac {f(x)}{x}},$; $b=\lim _{x\to \infty }(f(x)-ax).$
証明

直線 $y = ax + b$ は $x \to \infty$ でグラフ $y = f (x)$ に漸近するから、

(*)\quad \lim _{x\to \infty }\{f(x)-(ax+b)\}=0

が成り立つ。左辺の式を $x$ で割った式は、尚のこと $0$ に近付くから、

\lim _{x\to \infty }{\frac {f(x)-(ax+b)}{x}}=0.

ここで

\lim _{x\to \infty }{\frac {b}{x}}=0

であるから、

a=\lim _{x\to \infty }{\frac {f(x)}{x}}.

$(*)$ より、

b=\lim _{x\to \infty }(f(x)-ax)

である。■

この等式より、 $x \to \pm\infty$ で漸近する直線は、 $x \to \infty$ と $x \to -\infty$ にそれぞれ1つである。

$x$ 軸平行の漸近線[編集]

とくに $x$ 軸平行の漸近線は、前節の $a = 0$ の場合であり、漸近線 $y = b$ は

\lim _{x\to \infty }f(x)=b

または

\lim _{x\to -\infty }f(x)=b

で与えられる。

例えば、逆正接関数 $y = arctan x$ では、

{\begin{aligned}\lim _{x\to \infty }\arctan x&={\frac {\pi }{2}},\\\lim _{x\to -\infty }\arctan x&=-{\frac {\pi }{2}}\end{aligned}}

より、 $y = \pm π / 2$ は漸近線である。

分数関数の漸近線[編集]

分数関数の漸近線の方程式は、上記の方法を使わずに求めることができる。

分数関数の式を $y = g (x) / h (x)$ （既約分数式）とする。

$y$ 軸平行の漸近線

$h (a i) = 0$ を満たす $a i$ を求める ( $i = 1,2, \dots, n$ )。既約より $g (a i) \neq 0$ で、 $x = a i$ が漸近線である。

$x \to \pm\infty$ で漸近する直線

存在する必要十分条件は $deg g - deg h \leq 1$ である。このとき $g (x) \div h (x)$ の商 $q (x)$ , 余り $r (x)$ を求める。 $deg q \leq 1$ であり、直線 $y = q (x)$ が $x \to \pm\infty$ で漸近する直線である。

（例）

y={\frac {x^{3}+2x^{2}-2x+2}{x^{2}-x}}=x+3+{\frac {x+2}{x(x-1)}}

漸近線は、 $y$ 軸平行の漸近線は $x = 0$ , $x = 1$ 、 $x \to \pm\infty$ で漸近する直線は $y = x + 3$ である。

$deg g - deg h$ の値によって、漸近線の位置が分類される。

分数関数の $x \to \pm\infty$ で漸近する直線
$deg g - deg h$	$x \to \pm\infty$ で漸近する直線	分数関数， $x \to \pm\infty$ で漸近する直線の例
$< 0$	$y = 0$	${\frac {1}{x^{2}+1}},\,y=0$
$= 0$	$y = q (\neq 0)$	${\frac {2x^{2}+7}{3x^{2}+x+12}},\,y={\frac {2}{3}}$
$= 1$	$y = ax + b (a \neq 0)$	${\frac {x^{2}+x+1}{x}},\,y=x+1$
$> 1$	存在しない	${\frac {2x^{4}}{3x^{2}+1}}$ , なし

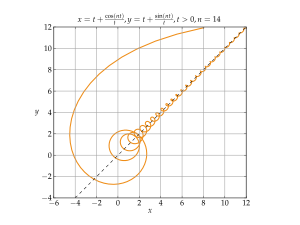
媒介変数表示された曲線の漸近線[編集]

媒介変数表示された平面曲線

C\colon (\alpha ,\beta )\to \mathbb {R} ^{2},\;t\mapsto (x(t),y(t))

を考える（ここで、 $α$ は $-\infty$ でもよく $β$ は $\infty$ でもよい）。曲線 $C$ は無限遠点に向かう、すなわち

\lim _{t\to \beta -}\|C(t)\|=\infty \quad {\text{i.e.}}\ \lim _{t\to \beta -}(x^{2}(t)+y^{2}(t))=\infty

が成り立つことを仮定する。直線 $l$ が曲線 $C$ の漸近線であるとは、 $t \to β -$ のとき点 $C (t)$ と直線 $l$ の距離が $0$ に収束することと定義される^[5]^[6]。

一般に、点 $C (t) = (x (t), y (t))$ と直線 $l : ax + by + c = 0$ の距離は

{\frac {|ax(t)+by(t)+c|}{\sqrt {a^{2}+b^{2}}}}

で与えられるので、直線 $l$ が曲線 $C$ の漸近線であるとは、

(**)\quad \lim _{t\to \beta -}(ax(t)+by(t)+c)=0

が成り立つことと同値である。曲線の媒介変数表示は一意ではないが、漸近線の定義はその取り方に依らない。実際、 $γ (t)$ を媒介変数の取り換えとすると、 $(**)$ は

\lim _{t\to \beta -}(ax(\gamma (t))+by(\gamma (t))+c)=0

と同値であるからである。

実一変数の実数値関数のグラフは、媒介変数表示された平面曲線の特別な場合と考えることができる。関数 $y = f (x)$ のグラフは点 $(x, f (x))$ の集合であり、 $x$ を径数 $t$ とすれば、径数付け（の一つ）

(\alpha ,\beta )\rightarrow \mathbb {R} ^{2},\;t\mapsto (t,f(t))

が得られる。

例えば、曲線 $y = 1 / x$ の右上の枝は媒介変数 $t$ により $x = t, y = 1 / t (t > 0)$ と表示できる。まず、 $t \to \infty$ のとき $x \to \infty$ であり、曲線上の点と $x$ 軸の距離 $1 / t$ は $t \to \infty$ のとき $0$ に収束する。したがって、 $x$ 軸は曲線の漸近線である。また、 $t \to 0+$ のとき、 $y \to \infty$ であり、このとき曲線上の点と $y$ 軸の距離 $t$ は $0$ に収束する。したがって $y$ 軸も漸近線である。同様に、曲線の左下の枝も同じ2本の直線が漸近線であることが示される。

関数のグラフでは、垂直でない漸近線は $x \to \pm\infty$ にそれぞれ高々1本ずつに限られるが、媒介変数表示から定まる一般の曲線は、垂直でない漸近線を3本以上持つこともあるし、1つの垂直な漸近線と2回以上交わる場合もある。

代数曲線の漸近線[編集]

曲線である漸近線[編集]

漸近線の定義に直線であることを仮定しない場合もある。曲線によっては曲線である漸近線も考えた方が形をとらえやすいことがある。

例えば、曲線

{\begin{aligned}y&={\frac {x^{3}+2x^{2}+3x+4}{x}}\\&=x^{2}+2x+3+{\frac {4}{x}}\end{aligned}}

は、放物線 $y = x 2 + 2 x + 3$ に $x \to \pm\infty$ で漸近する。

脚注[編集]

^ "Asymptotes" by Louis A. Talman
^ 数研通信80号（2014年9月） (PDF)
^ Williamson, Benjamin (1899), “Asymptotes”, An elementary treatise on the differential calculus
^ Nunemacher, Jeffrey (1999), “Asymptotes, Cubic Curves, and the Projective Plane”, Mathematics Magazine 72 (3): 183–192, doi:10.2307/2690881, JSTOR 2690881, https://jstor.org/stable/2690881
^ 青本和彦、上野健爾、加藤和也、神保道夫『岩波数学入門辞典』岩波書店、2005年9月29日。ISBN 978-4000802093。
^ Pogorelov, A. V. (1959), Differential geometry, Translated from the first Russian ed. by L. F. Boron, Groningen: P. Noordhoff N. V., MR0114163 , §8.

参考文献[編集]

[1] "Asymptotes" by Louis A. Talman

[2] 数研通信80号（2014年9月） (PDF)

[3] Williamson, Benjamin (1899), “Asymptotes”, An elementary treatise on the differential calculus

[4] Nunemacher, Jeffrey (1999), “Asymptotes, Cubic Curves, and the Projective Plane”, Mathematics Magazine 72 (3): 183–192, doi:10.2307/2690881, JSTOR 2690881, https://jstor.org/stable/2690881

[5] 青本和彦、上野健爾、加藤和也、神保道夫『岩波数学入門辞典』岩波書店、2005年9月29日。ISBN 978-4000802093。

[6] Pogorelov, A. V. (1959), Differential geometry, Translated from the first Russian ed. by L. F. Boron, Groningen: P. Noordhoff N. V., MR0114163 , §8.

[1]

[2]

[3]

[4]

[5]

[6]