グラフ (関数)
関数のグラフ(英: graph)は、直観的には、関数を平面内の曲線もしくは空間内の曲面としてダイアグラム状に視覚化したものである。形式的には、関数 f のグラフとは、順序対 (x, f(x)) の集合である。
例えば、x と f(x) が常に実数であるような関数の場合、グラフは座標平面上の点の集まりとみなすことができる。このような関数のうち、応用上重要な関数の多くは、グラフを座標平面上に曲線として描くことが可能である。
グラフの概念は、関数のみならず、より一般の写像や対応に対しても定義される。標語的には、グラフは関数や対応を特徴付ける集合であるといえる。
定義[編集]
f を、集合 A から集合 B への関数とする。すなわち、A の各元 x に対し、B の元 f(x) がただ一つ定まるとする。このとき、f のグラフとは、直積集合 A × B の部分集合
である。逆に、A × B の部分集合 G が、「任意の x ∈ A に対して (x, y) ∈ G なる元がただひとつ存在する」という条件を満たすならば、G をグラフとする A から B への関数 f が一意的に定まる。
特に、実数 x に対し、ただ一つの実数 f(x) が定まる関数 f を考えると、これは、A と B がともに実数全体の集合 R の場合である。このとき、グラフは R × R(R2 と表す)の部分集合である。R2 は2次元ユークリッド空間、すなわち平面と同一視され、この場合の関数のグラフは平面内の点の集まりとみなすことができる。
また、二つの実数 x, y に対し、ただ一つの実数 f(x, y) が定まる2変数関数 f を考えると、これは、A = R2 かつ B = R の場合である。このとき、グラフは R2 × R の部分集合である。R2 × R の元は ((x, y), z) の形をしているが、これを (x, y, z) と同一視することにより、グラフは3次元ユークリッド空間 R3 内の点の集まりとみなすことができる。
具体例[編集]


関数
のグラフは {(a, 2), (b, 0), (c, −1)} である。このグラフを視覚化するルールは、標準的には定まっていないが、棒グラフ等で表すことは可能である。
実数上の三次関数
- f(x) = x3 − 9x
のグラフは {(x, x3 − 9x) | x ∈ R} である。座標平面上で、各 x に対して (x, x3 − 9x) をプロットすると、右の曲線を得る。一般には、この曲線を指して f のグラフと称することが多い。
実数上の2変数関数
- f(x, y) = x2 − y2
のグラフは {(x, y, x2 − y2) | x, y ∈ R} である。座標空間内で、各 (x, y) に対して (x, y, x2 − y2) をプロットすると、右の曲面を得る。
R から R への関数だとしても、実際にグラフを描画できるとは限らない。例として、ディリクレの関数、すなわち有理数に対しては 1 を、無理数に対しては 0 を対応させる関数を考える。
この関数のグラフは、2本の平行な直線に「見える」であろう。しかし、それぞれの直線には無数に穴が空いているのであり、これを正確に描画することは不可能である。
関数の性質とグラフの特徴[編集]
本節では、簡単のため、R から R への関数のみを考え、関数の性質とグラフの特徴の関係について述べる。
関数の定義・全射性・単射性[編集]
関数の定義より、任意の実数 x に対して f(x) がただ一つ定まるため、x 軸に垂直な直線は、関数のグラフとただ1点で交わる。一方、y 軸に垂直な直線は、グラフと交わらないことも、複数の点で交わることもある。y 軸に垂直な直線とグラフが交わる回数は、関数の全射性や単射性と対応している。
連続性[編集]
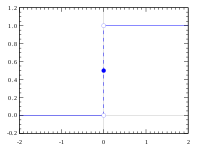
関数 f が x = a で連続であるとは、おおまかには、f のグラフが (a, f(a)) の周辺で「つながっている」ということである。例えば、ヘヴィサイドの階段関数は、x = 0 でのみ不連続であって、他の点では連続である。
しかし、数学における連続性は、厳密には極限、ひいてはε-δ論法を用いて定義されるのであって、必ずしも直感的に分かりやすい例ばかりではない。分かりにくい例として、次の関数 f を考える。
この関数のグラフは、2本の直線が (1/2, 1/2) で直交しているように「見える」が、ディリクレの関数と同様に無数に穴が空いている。連続性の定義から、x = 1/2 でのみ連続であって、他の点では不連続である。
微分可能性[編集]
関数 f が x=a で微分可能であるとは、おおまかには、 f のグラフが (a,f(a)) の周辺で「滑らか」であって、その点における接線が描けるということである。例えば、絶対値関数は、x=0 でのみ微分不可能であって、他の点では微分可能である。なお、微分可能ならば連続でもあるが、逆は成り立たない。
微分可能性は、やはり極限を用いて定義されるのであって、必ずしも直感的に分かりやすい例ばかりではない。例として、次の関数 f1 を考える。この関数のグラフは、原点の近くで無限回振動しており、正確に描くことはできない。
f1 は x=0 で連続ではあるが、微分可能ではない。このことは、グラフの外見だけからは判別しにくい。
似た定義式であっても、次の関数は x=0 で微分可能である。
なお、導関数 f2′は x = 0 で不連続である。
-
絶対値関数は原点で微分不可能
-
f1 は原点で微分不可能
-
f2 は原点で微分可能
陰関数のグラフ[編集]
陰関数表示されたグラフはy=±√・・・の形の陽関数にして書く。
対称性を見つければy=±√・・・のプラスマイナスは片方だけ調べればよくなる[1]。
脚注[編集]
- ^ “陰関数表示された関数のグラフの書き方 | 数学の偏差値を上げて合格を目指す”. 数学の偏差値を上げて合格を目指す (2017年10月5日). 2022年3月17日閲覧。
関連項目[編集]
外部リンク[編集]
- Weisstein, Eric W. "Function Graph". mathworld.wolfram.com (英語).









