無理数
無理数(むりすう、 英: irrational number)とは、有理数ではない実数、つまり整数の比(英: ratio)(分数)で表すことのできない実数のことである。実数は非可算個で有理数は可算個であるから、無理数は非可算個あり、ほとんど全ての実数は無理数である。
無理数という語は、何かが「無理である数」という意味に受け取れるため、語義的に「無比数」と訳すべきだったという意見もある[1][2][3](有理数#用語の由来も参照)。
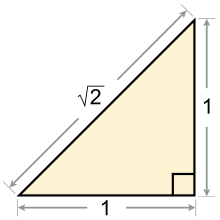
無理数の例[編集]
以下の実数は無理数である。
- 平方数を除く平方根( 、など)
- 整数 N の m 乗根 (ただし、m は 1 より大きい整数、N は m 乗数でない整数)
- 対数 logm n(ただし、m, n は 1 より大きい整数で、m = Na, n = Nb を満たす整数 N, a, b が存在しない)
- log2 3 や log2 5
- 三角関数の零でない有理数 x における値[4] cos x, sin x, tan x, csc x, sec x, ctn x
- 円周率 π
- ネイピア数 e
- ゲルフォントの定数 eπ
- アペリーの定数 ζ(3)
- 小数部分が循環しない無限小数で表される数。例えば十進法における
- チャンパーノウン定数 0.123456789101112…(小数部分に自然数を順に並べた小数)
- コープランド-エルデシュ定数 0.2357111317192329…(小数部分に素数を順に並べた小数)
無理数判定法[編集]
任意の ε > 0 に対して不等式
が有理数解 p/q を持つとき、α は無理数である。多くの無理性の証明はこれを用いている。これは α が無理数であるための必要十分条件でもある。
性質[編集]
無理数を十進小数で表記すると、繰り返しのない無限小数(非循環小数)になる。これは記数法の底によらず一般の N 進小数でも成り立つ。
α を無理数とすると、
を満たす無限に多くの有理数 p/q が存在する(ディリクレの定理)。なお、このように無理数の有理数による近似を扱う理論はディオファントス近似と呼ばれる数論の分野に属する。
無理数全体の空間を完備とするような距離が存在する。またA-演算が自然に応用できる例でもあり、この空間は点集合論的トポロジーでは重要な対象である。
代数的無理数と超越数[編集]
無理数のうち、代数的数であるものを代数的無理数、そうでないものを超越数という。
α が代数的数、κ > 2 ならば、
を満たす有理数 p/q は有限個しかない(トゥエ-ジーゲル-ロスの定理)[5]。このことは不定方程式の解の有限性を示すときに使われる。
2の平方根は代数的無理数であり、log2 3, e, π, eπ といった数は超越数である。ζ(3) が超越数であるか否かは未だに解決されていない。
無理数度[編集]
数 α に対して
を満たす有理数 p/q は有限個しかない、という性質を満たす κ の下限を α の無理数度 (英: irrationality measure) という。
有理数の無理数度は 1, ディリクレの定理およびロスの定理より代数的無理数の無理数度は 2, リウヴィル数の無理数度は ∞ である。ディリクレの定理より無理数の無理数度は全て 2 以上である。e の無理数度は 2 であることが知られている。また、πの無理数度の上限は7.103程度であることがわかっている[6]。
ルベーグ測度に関してほとんど全ての数の無理数度は 2 である。
歴史[編集]
無理数の発見は古代ギリシア文明にまで遡る。一説では、無理数の発見者は古代ギリシャの大数学者、ピタゴラスの弟子であったヒッパソスという人物であった。ヒッパソスは正方形の研究をしているうち、その辺と対角線の長さの比は整数でも分数でも表せない未知の数、すなわち無理数であることを発見したという。
彼の師匠のピタゴラスは、宇宙の万物は数から成り立つこと、そして宇宙を構成する数は、調和した比を保っていると信じていた。ピタゴラスと教団は教義の反証である無理数が存在する事実に動揺し、不都合な事実を隠すため、発見者のヒッパソスを縛りあげ、船から海に突き落として殺害したという伝承が残っている。
しかし、プラトンが現れると、彼の著書『テアイテトス』の中で平方数でない数の平方根が有理数でないことを論じ、さらに同じ論法が立方根にも適用できると述べている。これらの数学的な蓄積を受けて、エウクレイデスは『原論』の中で統一した形で実数論を展開している。
円周が円の直径の3倍より少し大きいことは古来知られていた。古代インドやギリシアの数学者たちの間では半径 r の円の面積が円周率 π を使って πr2 であることも知られ、アルキメデスは半径 r の球の体積が 4/3πr3 であることや、この球の表面積が 4πr2 (その球の大円の面積の4倍)であることを示していた。円周率 π が無理数であることはすでにアリストテレスによって予想されていたが、実際に証明されたのはそれよりはるかに後の時代のことである(ヨハン・ハインリヒ・ランベルト)。
自然対数の底であるネイピア数 e は、1618年にジョン・ネイピアが発表した対数の研究の付録の表にその端緒があるが、定性的に研究したのはレオンハルト・オイラーである。
1872年にリヒャルト・デデキントは『連続性と無理数』を出版し、デデキント切断を用いて無理数を定義した。
リーマンゼータ関数の特殊値 ζ(3) は、アペリーによって1979年に無理数であることが証明された(アペリーの定数)。π + eπ は、ネステレンコによって無理数であることが証明された。
未解決の問題[編集]
オイラーの定数(オイラー・マスケローニ定数)γ、π+e、eπ、その他 P (e, π) の形であらわされる数(ここで P (x, y) は、x, y 双方について次数が 1 以上の多項式を表す)はいずれも、有理数であるか無理数であるか知られていない。
また、ee、πe、ππ、といった数もやはり、有理数であるか無理数であるか知られていない。ただし、上記 #無理数の例 に挙げたとおり、eπ は無理数であることが既に知られている。
脚注[編集]
- ^ 堀場芳数『無理数の不思議』講談社、1993年 ISBN 978-4061329782
- ^ 吉田武『オイラーの贈物 人類の至宝eiπ=-1を学ぶ』東海大学出版会、2010年 ISBN 978-4486018636
- ^ 吉田武『虚数の情緒 中学生からの全方位独学法』東海大学出版会、2000年 ISBN 978-4486014850
- ^ Niven 2005, p. 21.
- ^ ピーター・フランクル『ピーターフランクルの中学生でも分かる大学生にも解けない数学問題集1』日本評論社、2001年、10頁。ISBN 4-535-78262-8。
- ^ Irrationality Measure
参考文献[編集]
- 塩川宇賢:『無理数と超越数』森北出版、ISBN 978-4627060913、(1999年)。
- デーデキント『数について 連続性と数の本質』河野伊三郎訳、岩波書店、ISBN 4-00-339241-8、(1961年)。
- W. M. Schmidt, "Diophantine Approximations", Lecture Notes in Math. 785, Springer-Verlag, 1980.
- W. M. Schmidt, "Diophantine approximations and diophantine equations", Lecture Notes in Math. 1467. Springer-Verlag, 1991.
- R. Apéry, "Irrationalité de ζ(2) et ζ(3)", Astérisque 61(1979), 11-13.
- A. van der Poorten, "A Proof that Euler Missed... Apéry's Proof of the Irrationality of ζ(3)", Math. Intel. 1 (1979), 196-203.
- ジュリアン・ハヴィル、松浦俊輔(訳):「無理数の話 √2の発見から超越数の謎まで」青土社、ISBN 978-4791766758、(2012年10月24日)。
- 西岡久美子:「超越数とはなにか 代数方程式の解にならない数たちの話」講談社(ブルーバックス)ISBN 978-4062579117(2015年4月21日)。
- I. Niven (2005). Irrational Numbers. The Mathematical Association of America. ISBN 0-88385-038-9
関連文献[編集]
- 高木貞治、1904「第九章 無理數」『新式算術講義』
関連項目[編集]
外部リンク[編集]
 ウィキソースには、新式算術講義/第九章の原文があります。
ウィキソースには、新式算術講義/第九章の原文があります。 ウィクショナリーには、無理数の項目があります。
ウィクショナリーには、無理数の項目があります。- Weisstein, Eric W. "Irrational Number". mathworld.wolfram.com (英語).



![{\displaystyle {\sqrt[{m}]{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e38d4ea6b80d5e7018cfea36a7467e51d1631d)







![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)





