行列の乗法
数学において、行列の対から別の行列を作り出す二項演算としての行列の乗法(ぎょうれつのじょうほう)は、実数や複素数などの数が初等的な四則演算でいうところの乗法を持つことと対照的に、そのような「数の配列」の間の乗法として必ずしも一意的な演算を指しうるものではない。そのような意味では、一般に「行列の乗法」は幾つかの異なる二項演算を総称するものと考えることができる。行列の乗法の持つ重要な特徴には、与えられた行列の行および列の数(行列の型やサイズあるいは次元と呼ばれるもの)が関係して、得られる行列の成分がどのように特定されるかが述べられるということが挙げられる。
例えば、ベクトルの場合と同様に、任意の行列に対してスカラーを掛けるという操作が、その行列の全ての成分に同じ数を掛けるという方法で与えられる。また、加法や減法の場合と同様に、同じサイズの行列に対して成分ごとの乗法を入れることによって定まる行列の積はアダマール積と呼ばれる。それ以外にも、二つの行列のクロネッカー積は区分行列として得られる。
このようにさまざまな乗法が定義できるという事情の中にあっても、しかし最も重要な行列の乗法は連立一次方程式やベクトルの一次変換に関するもので、応用数学や工学へも広く応用がある。これは通例、行列の積(ぎょうれつのせき、英: matrix product[1][2])と呼ばれるもので、A が n × m 行列で、B が m × p 行列ならば、それらの行列の積 AB が n × p 行列として与えられ、その成分は A の各行の m 個の成分がそれぞれ順番に B の各列の m 個の成分と掛け合わされる形で与えられる(後述)。
この通常の積は可換ではないが、結合的かつ行列の加法に対して分配的である。この行列の積に関する単位元(数において 1 を掛けることに相当するもの)は単位行列であり、正方行列は逆行列(数における逆数に相当)を持ち得る。行列の積に関して行列式は乗法的である。一次変換や行列群あるいは群の表現などの理論を考える上において行列の積は重要な演算となる。
行列のサイズが大きくなれば、二つあるいはそれ以上の行列の積の計算を定義に従って行うには、非常に膨大な時間が掛かるようになってしまうため、効果的に行列の積を計算できるアルゴリズムが考えられてきた。
スカラー倍
[編集]行列に付随するもっとも単純な形の乗法としてスカラー乗法が挙げられる(これはクロネッカー積の特別の場合になっている)。
行列 A のスカラー λ による左スカラー倍(英: left scalar multiplication)は、
で与えられる A と同じサイズの行列 λA となる。つまり、
同様に、行列 A のスカラー λ による右スカラー倍(英: right scalar multiplication)は
で定義される。
基礎とする環が(例えば実または複素数体のような)可換環ならば、左及び右スカラー倍の概念は一致して、単にスカラー倍と呼ばれる。より一般の環では(四元数体のように)非可換であるから左右が異なれば異なる乗法である。
通常の行列の積
[編集]二つの行列の積
[編集]まずは二つの行列を掛け合わせることを考える(任意個数への一般化は後述)。
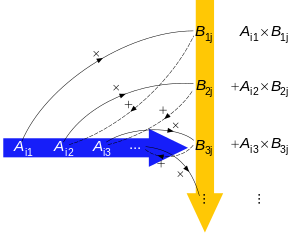
n × m 行列 A と m × p 行列 B を
とするとき、これらの行列の積 AB(通例、乗法記号は特に用いずに併置で表す)は、 各 (i, j) 成分 cij が A の第 i 行に横に並ぶ成分 aik と B の第 j 列に縦に並ぶ成分 bkj を k = 1, 2, ..., m に亙って足し合わせた和
で与えられる n × p 行列
である[3][4][5][6]。従って、積 AB が定義されるのは A の列の本数と B の行の本数が一致している場合に限られる(今の場合は m 本)。
多数の行列の積
[編集]二つ以上の個数の行列に対しても、それらの連続する各対に関してサイズの条件が満たされるならば、行列の積を定義することができる。
n-個の行列 A1, A2, ..., An がそれぞれサイズ s0 × s1, s1 × s2, ..., sn − 1 × sn であるとき(ここで s0, s1, s2, ..., sn は何れも単に正整数であって、これらの下付き添数はそれぞれどの行列に対応するのかを示す以上の意味は無い)、これら行列の積
は s0 × sn 行列であり、その任意の (i0, in)-成分は
で与えられる。
行列の冪
[編集]正方行列に関しては、行の本数と列の本数が常に等しいから、通常の数と同様に自分自身を繰り返し掛けることができて、この行列の積の特別の場合としての反復乗積は行列の冪(英: matrix power)を定義することができる。行の本数と列の本数が一致しない一般の矩形行列では冪を考えることができない。即ち、n × n 行列 A と正整数 k に対して
冪の逆として行列の冪根を考えたり、また冪級数として行列の指数函数やその逆写像として行列の対数函数などを定義したりすることもできる。
その他の乗法
[編集]二つの行列に対して定義されるその他の乗法を以下にいくつか挙げる。実は通常の乗法よりも定義としては単純なものもいくつかある。
アダマール積
[編集]同じサイズの二つの行列に対し、アダマール積(英: Hadamard product)、要素ごとの積(英: element-wise product)、点ごとの積(英: pointwise product)、成分ごとの積(英: entrywise product)あるいはシューア積(英: Schur product)などと呼ばれる積を定義することができる[7]。同じサイズの二つの行列 A, B のアダマール積 A ○ B はもとと同じサイズの行列で、その (i, j)-成分は A の (i, j)-成分と B の (i, j)-成分との積で与えられる。つまり、
全部書けば、
この演算は(mn 個ある各成分において)通常の数の積を一斉に行うことに他ならない。故にアダマール積は可換、結合的、かつ成分ごとの和に対して分配的になる。これはまた、クロネッカー積の主小行列でもある。
フロベニウス積
[編集]フロベニウス(内)積(英: Frobenius inner product)は行列を単にベクトルと見做してとった成分ごとの内積で、A : B などと書かれることもある。これはアダマール積の成分の和でもあり、具体的に書けば
となる。ただし "tr" は行列の蹟であり、"vec" は行列の一列化である。この内積からフロベニウスノルムが誘導される。
クロネッカー積
[編集]二つの行列 A, B のサイズがそれぞれ m × n, p × q であるとき、これらがどのようなサイズであったとしても(サイズに関する制約条件なしに)、この二つの行列のクロネッカー積(英: Kronecker product)は
で与えられるサイズ mp × nq の行列である[8]。これはより一般のテンソル積を行列に対して適用したものになっている。
注
[編集]- ^ R.G. Lerner, G.L. Trigg (1991). Encyclopaedia of Physics (2nd ed.). VHC publishers. ISBN 3-527-26954-1
- ^ C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). ISBN 0-07-051400-3
- ^ S. Lipschutz, M. Lipson (2009). Linear Algebra. Schaum's Outlines (4th ed.). McGraw Hill (USA). pp. 30–31. ISBN 978-0-07-154352-1
- ^ K.F. Riley, M.P. Hobson, S.J. Bence (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3
- ^ R. A. Adams (1995). Calculus, A Complete Course (3rd ed.). Addison Wesley. p. 627. ISBN 0 201 82823 5
- ^ Horn, Johnson (2013). Matrix Analysis (2nd ed.). Cambridge University Press. p. 6. ISBN 978 0 521 54823 6
- ^ (Horn & Johnson 1985, Ch. 5)
- ^ Steeb, Willi-Hans (1997), Matrix Calculus and Kronecker Product with Applications and C++ Programs, World Scientific, p. 55, ISBN 9789810232412.
参考文献
[編集]- Henry Cohn, Robert Kleinberg, Balazs Szegedy, and Chris Umans. Group-theoretic Algorithms for Matrix Multiplication. arXiv:math.GR/0511460. Proceedings of the 46th Annual Symposium on Foundations of Computer Science, 23–25 October 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379–388.
- Henry Cohn, Chris Umans. A Group-theoretic Approach to Fast Matrix Multiplication. arXiv:math.GR/0307321. Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, 11–14 October 2003, Cambridge, MA, IEEE Computer Society, pp. 438–449.
- Coppersmith, D., Winograd S., Matrix multiplication via arithmetic progressions, J. Symbolic Comput. 9, p. 251-280, 1990.
- Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1
- Knuth, D.E., The Art of Computer Programming Volume 2: Seminumerical Algorithms. Addison-Wesley Professional; 3 edition (November 14, 1997). ISBN 978-0-201-89684-8. pp. 501.
- Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), Cambridge University Press, ISBN 978-0-521-88068-8.
- Ran Raz. On the complexity of matrix product. In Proceedings of the thirty-fourth annual ACM symposium on Theory of computing. ACM Press, 2002. doi:10.1145/509907.509932.
- Robinson, Sara, Toward an Optimal Algorithm for Matrix Multiplication, SIAM News 38(9), November 2005. PDF
- Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969.
- Styan, George P. H. (1973), “Hadamard Products and Multivariate Statistical Analysis”, Linear Algebra and its Applications 6: 217–240, doi:10.1016/0024-3795(73)90023-2
- Vassilevska Williams, Virginia, Multiplying matrices faster than Coppersmith-Winograd, Manuscript, May 2012. PDF













