 選り抜き記事
選り抜き記事
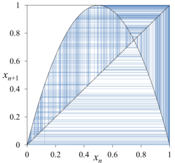
ロジスティック写像とは、xn+1 = axn(1 − xn) という2次関数の差分方程式(漸化式)で定められた離散力学系である。単純な2次関数の式でありながら、驚くような複雑な振る舞いが生み出される。特に数理生物学者ロバート・メイの研究によってロジスティック写像は広く知られるようになり、生物の個体数の変化を表すモデルとしても知られる。
適当にパラメータ a の値を決め、最初の変数 x0 を決めて計算すると、x0, x1, x2, … という軌道が得られる。a を変化させると、ロジスティック写像の軌道は、一つの値へ落ち着いたり、いくつかの値を周期的に繰り返したり、カオスと呼ばれる非周期的変動を示したりと様々に変化する……
- ニヴフは、主としてロシアに住む少数民族。その多くは樺太(サハリン州)、アムール川(黒竜江)下流域に住んでいる。1979年の人口は約4,400人。アイヌとも、ツングース・満洲系諸族やモンゴル系民族とも系統の異なる民族であり……
- ウィルタは、ロシア連邦サハリン州の樺太(サハリン島)東岸を主な居住域とする少数民族で、ツングース系に属する。その生活の舞台は、伝統的には樺太中部の幌内川流域と北部のロモウ川流域であった。本来の言語はツングース諸語の系統である……
- 「ソリクン」は、韓国の男性アイドルグループStray Kidsの楽曲である。2021年8月23日にJYPエンターテインメントから発売された2作目のスタジオ・アルバム『NOEASY』に収録され、同作からの先行シングルとしても発売された……




