ロジスティック写像

ロジスティック写像の振る舞いをクモの巣図法で示した図。初期値を0.2としてパラメータ（図中の r）を 1 から 4 まで増やしたときに起こる振る舞いの変化がアニメーションで示されている。

ロジスティック写像（ロジスティックしゃぞう、英語: logistic map）とは、x_n+1 = ax_n(1 − x_n) という2次関数の差分方程式（漸化式）で定められた離散力学系である。ロジスティックマップや離散型ロジスティック方程式（英語: discrete logistic equation）とも呼ばれる。単純な2次関数の式でありながら、驚くような複雑な振る舞いを生み出すことで知られる。

ロジスティック写像の a はパラメータと呼ばれる定数、x が変数で、適当に a の値を決め、最初の x₀ を決めて計算すると、x₀, x₁, x₂, … という数列が得られる。この数列を力学系分野では軌道と呼び、軌道は a にどのような値を与えるかによって変化する。パラメータ a を変化させると、ロジスティック写像の軌道は、一つの値へ落ち着いたり、いくつかの値を周期的に繰り返したり、カオスと呼ばれる非周期的変動を示したりと様々に変化する。

ロジスティック写像を生物の個体数を表すモデルとして見る立場からは、変数 x_n は1世代目、2世代目…というように世代ごとに表した個体数を意味しており、ロジスティック写像とは現在の個体数 x_n から次の世代の個体数 x_n+1 を計算する式である。生物個体数モデルとしてのロジスティック写像は、ある生物の個体数がある環境中に生息し、さらにその環境と外部との間で個体の移出入がないような状況を想定しており、x_n は正確には個体数そのものではなく、その環境中に存在できる最大個体数に対する割合を意味する。微分方程式で個体数をモデリングするロジスティック方程式の離散化からもロジスティック写像は導出でき、「ロジスティック写像」という名もそのことに由来する。

2次関数の力学系としての研究は20世紀初頭からあったが、1970年代、特に数理生物学者ロバート・メイの研究によってロジスティック写像は広く知られるようになった。メイ以外にも、スタニスワフ・ウラムとジョン・フォン・ノイマン、ペッカ・ミュルバーク、オレクサンドル・シャルコフスキー、ニコラス・メトロポリスら、ミッチェル・ファイゲンバウムなどがロジスティック写像の振る舞い解明に関わる仕事を成している。

定義と背景

単純に言えば、ロジスティック写像とは次のような2次関数である。

$y=ax(1-x)$

(1-1)

式中の a は定数を意味し、パラメータと呼ばれる。a 以外には、μ や r や λ をパラメータの記号に使うこともある。

式 (1-1) に対して、まず定数 a の具体的な数値を決める。さらに変数 x の値を適当に決め、式から y の値を計算する。そして、得られた y の値を新しい x の値とみなして式に代入し、新しい y の値を計算する。このような計算を繰り返すことが、ロジスティック写像を使って行うことである。例として、a を 2、最初の x を 0.01 としたときの繰り返し計算を5回目まで行うと、以下の表のようになる。

a を 2、最初の x を 0.01 としたときに、ロジスティック写像の計算を繰り返した例
（小数点以下10桁までで計算）

計算回数	入力する x の値	y = 2x(1 − x) の計算結果
1	0.01	2 × 0.01 × (1 − 0.01) = 0.0198
2	0.0198	2 × 0.0198 × (1 − 0.0198) = 0.03881592
3	0.03881592	2 × 0.03881592 × (1 − 0.03881592) = 0.0746184887
4	0.0746184887	2 × 0.0746184887 × (1 − 0.0746184887) = 0.1381011397
5	0.1381011397	2 × 0.1381011397 × (1 − 0.1381011397) = 0.2380584298

ロジスティック写像自体は中学校で習うような何の変哲もない2次関数であり、計算自体も中学生でも可能である。繰り返しの計算も電卓ででき、コンピュータの表計算ソフトを使えばより簡単にできる。

ロジスティック写像は、漸化式あるいは差分方程式の形式で次のようにも書き表される。

$x_{n+1}=ax_{n}(1-x_{n})$

(1-2)

x₀ の値を決めると、この差分方程式にしたがい、その後の変数の値 x₁, x₂, x₃,… が順次に計算できる。このような数列を作る差分方程式を、力学系（ダイナミカルシステム）とも呼ぶ。力学系とは、時間とともに状態が変化する系（システム）のことで、とりわけ現在の状態が決まればその後の状態も一意的に決まる系を指す。差分方程式 (1-2) のような形式で定義される力学系はとくに離散力学系と呼ばれる。

力学系的な視点では、変数 x_n の下付き添え字 n を時刻や時間と呼ぶ。数列の最初の値 x₀ は初期値と呼ばれる。変数の時間変化の様子を、明確な専門用語ではないが振る舞いと呼ぶ。と言っても、時刻 n は物理的な時間を本当に意味しているわけではなく、何かしらの現象の進行を表している便宜的なラベルのようなものである。

後で詳述するように、ロジスティック写像は生き物の個体数の変化を考える式として世に広まった側面を持つ。この場合、x_n は、ある世代における生き物の個体数を、生息環境で可能な最大生息個体数で割った値を意味している。差分方程式 (1-2) によって、n 世代目の個体数から n+1 世代目の個体数が計算できるというのが、生物個体数モデルとしてのロジスティック写像の意味である。個体数が増えていくと、個体数の増加速度は下がってくるだろうから、この効果をロジスティック写像では (1 − x_n) という項で取り入れている。例えば、ある世代で個体数が最大生息個体数に近くて x_n = 0.9999 だとすれば 項 (1 − x_n) は 0 にとても近い数値になるので、次の世代の個体数 x_n+1 は急激に減ることになる。

「ロジスティック写像」の名の中に出てくる写像とは、ある集合の要素をまたある集合の要素に対応させる規則を指す用語である。関数に似たようなものだが、関数を数以外の集合も扱うような場合も含めてより一般化したのが写像といえる。写像という視点からは、ロジスティック写像は実数の1点を実数の1点へ対応させる規則だといえる。ただし、「関数」と「写像」に数学全体で共有されている厳密な呼び分けは存在しておらず、実際のところ、どちらの言葉を使うかは各分野の習慣に依るところが大きい。力学系分野では、式 (1-2) のような差分方程式を写像として捉え、写像という語で呼ぶことが多い。

ロジスティック写像を写像の形で表現すると、

$f:x\mapsto ax(1-x)$

(1-3)

や

$f(x)=ax(1-x)$

(1-4)

のように記される。写像がパラメータ a に依存していることを明確にするために、

$f_{a}(x)=ax(1-x)$

(1-5)

のように、写像の記号にパラメータ記号の添え字を付けて表すこともある。式 (1-3) や式 (1-4) のような写像としての表現は、式 (1-2) のような差分方程式の表現と実質的に同等だが、時刻 n を一々書き表さなくてもよい利便性もあってしばしば使われる。

離散力学系の数列 x₀, x₁, x₂,… は、写像 f を繰り返し適用して生み出されるという見方もできる。初期値を x₀ とすると、

${\begin{aligned}x_{1}&=f(x_{0})\\x_{2}&=f(f(x_{0}))\\x_{3}&=f(f(f(x_{0})))\end{aligned}}$

(1-6)

というように、数列は x₀ に写像を繰り返し適用して作られるものとしても書ける。このように写像を繰り返し適用する操作を写像の反復などと呼ぶ。簡単に表記するために、写像の反復を

${\begin{aligned}f(f(x_{0}))\ =f^{2}(x_{0})\\f(f(f(x_{0})))\ =f^{3}(x_{0})\end{aligned}}$

(1-7)

というように書く。fⁿ(x₀) で、x₀ に対する f の n 回反復を意味している。そして、差分方程式から生み出される

$x_{0},\ x_{1},\ x_{2},\cdots$

(1-8)

という列、あるいは写像の反復から生み出される

$x_{0},\ f(x_{0}),\ f^{2}(x_{0}),\cdots$

(1-9)

という列を、力学系では軌道と呼ぶ。力学系という分野の関心は、与えられた力学系の軌道の振る舞いを研究することにある。

入力と結果が単純な比例関係で結ばれているようなシステムを線形といい、比例関係で表すことができないようなシステムを非線形という。ロジスティック写像は、考えられる限りでもっとも単純な非線形関数である2次関数で定義される。しかし、その非常に簡単な式とは裏腹に、ロジスティック写像は非常に複雑な振る舞いを生み出す。2次関数の繰り返し計算という設定が現代的な数学の主題の一つであり、豊饒な数学理論を引き起こす。ロジスティック写像には「思いもよらぬ奥深い内容」「力学系で起こる数多くの最も重要な現象」、そして「信じられないような複雑な振舞い」が含まれている。後述するようにロジスティック写像ではカオスという現象が現れ、カオス入門の好適な題材でもある。

定義域とグラフ

ロジスティック写像のグラフ（x_n+1 と x_n の関係）。グラフは放物線の形をしており、パラメータ a が変わると放物線の頂点が変わる。

前述のように、ロジスティック写像には生物の個体数の変動を考えるモデルとしての側面がある。このとき、ロジスティック写像の変数 x は生物の個体数を最大生息数で割った値であったから、x が取り得る数値は 0 ≤ x ≤ 1 の間に限られる。そういった事情もあり、ロジスティック写像の変数の範囲を区間 [0, 1] に限って、その振る舞いが議論されることが多い。

変数を常に 0 ≤ x ≤ 1 に限定しようとすると、必然的にパラメータ a が取れる範囲は 0 から 4 まで (0 ≤ a ≤ 4) に限定される。なぜならば、x_n が [0, 1] の範囲内にあれば、x_n+1 の最大値は a/4 となっている。したがって、a > 4 では x_n+1 の値が 1 を超える可能性が出て来てしまう。一方、a が負のときは、x が負の値を取るようになってしまう。

写像のグラフを利用することで、その振る舞いの多くを知ることもできる。ロジスティック写像 x_n+1 = ax(1 − x_n) のグラフとは、横軸を x_n（あるいは x）とし、縦軸を x_n+1（あるいは f (x)）として、平面上に x_n と x_n+1 の関係を示した曲線である。ロジスティック写像のグラフは、a = 0 の場合を除き、

$(x_{n},x_{n+1})=\left(0.5,{\frac {a}{4}}\right)$

(2-1)

を頂点とする放物線の形をしている。a を変化させると頂点は上下に動き、放物線は形を変える。また、ロジスティック写像の放物線は横軸（x_n+1 = 0 の直線）と2点で交わる。(x_n, x_n+1) = (0, 0) と (x_n, x_n+1) = (1, 0) がその2つの交点で、これらの交点の位置は a の値に影響されず一定である。

ロジスティック写像のグラフ上で、クモの巣図法によった軌道を描いた例。また、グラフ上の不動点 x_f 1, x_f 2 の位置。

写像のグラフは、とくにロジスティック写像のような1変数の写像のグラフは、その写像の振る舞いを理解するための鍵である。グラフの効能の一つは、不動点と呼ばれる点の図示である。写像のグラフに重ねるように y = x の直線（45°の直線）を引く。この45°直線とグラフが交わる点があれば、その点が不動点である。式で書くと、不動点とは

$f(x)=x$

(2-2)

を満たしている点であり、写像を適用しても変化しない点を意味する。不動点を x_f と表記することにする。ロジスティック写像の場合に式 (2-2) を満たす不動点は、ax(1 − x) = x を解いて、

$x_{f1}=0$

(2-3)

$x_{f2}=1-{\frac {1}{a}}$

(2-4)

の2点である（a = 0 の場合を除く）。不動点の概念は離散力学系において最も重要となる。

1変数写像に対して使えるもう一つのグラフを利用した技術が、クモの巣図法と呼ばれる手法である。横軸上に初期値 x₀ を決めた後に、そこから f (x) の曲線まで縦向きに直線を引く。f (x) の曲線にぶつかったところから y = x の45°直線まで横向きに直線を引き、45°直線にぶつかったところから f (x) の曲線まで縦向きに直線を引く。これを繰り返すことで、平面上にクモの巣状ないし階段状の図ができる。実はこの作図は図示的に軌道の計算を行ってることに等しく、作成されたクモの巣状の図は x₀ から出発する軌道を表している。この図法によって、軌道の全体的な振る舞いを一目で見ることができる。

振る舞い、パラメータ a による変化

ロジスティック写像のパラメータ（図中では r）を 0.02 から 4 まで変化させたときの振る舞いの変化を示したアニメーション。横軸が繰り返し数 n（図中では t）、縦軸が x で、繰り返し計算 200 回までの x を図示している。

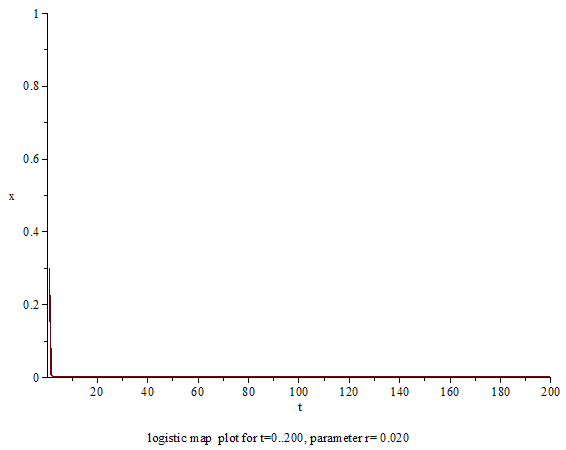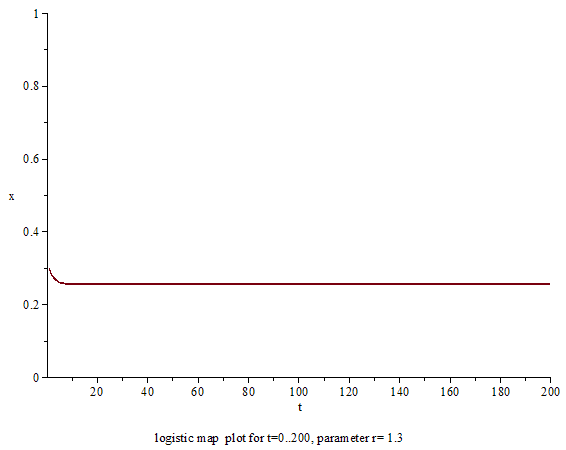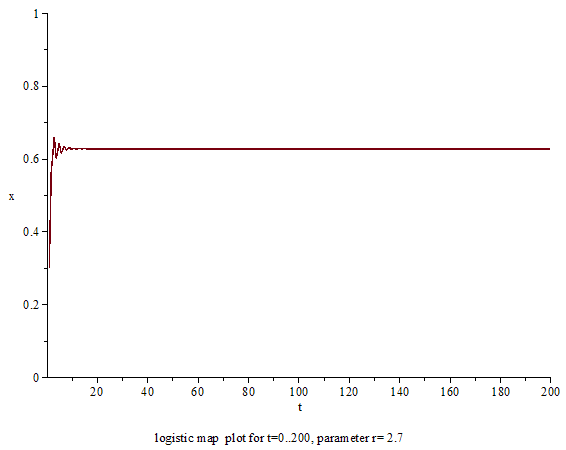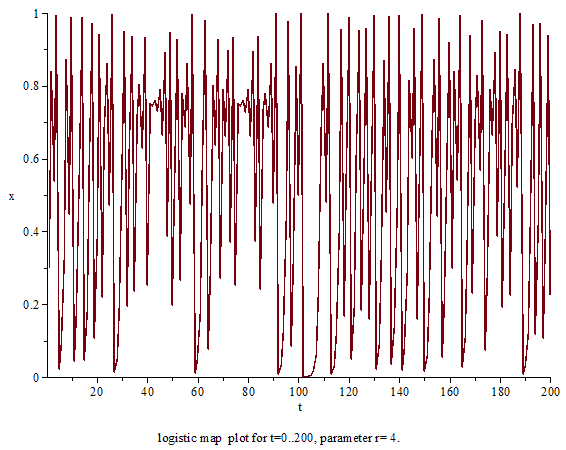
上述のように、ロジスティック写像自体は何の変哲もない2次関数であり、軌道の計算自体も中学生でも可能である。力学系的に重要な問題は、パラーメータ a を変化させると軌道の振る舞いがどう変わるのかにある。a の数値によって、ロジスティック写像の軌道の振る舞いは単純にも複雑にも変わる。以下、a を増やしていったときに、ロジスティック写像の振る舞いがどのように変化していくかを順に説明する。

0 ≤ a < 1 のとき

まず、パラメータが a = 0 のときは、初期値 x₀ がどんな値であろうが、x₁ = 0 となる。つまり、a = 0 におけるロジスティック写像の軌道は、初期値以降の値が全て 0 となるような軌道で、この場合あまり調べる中身はない。

次に、パラメータが 0 < a < 1 の範囲にあるとき、初期値 x₀ が 0 から 1 までのどんな数値であったとしても、x_n は単調に減少していく。つまり、n → ∞ の極限で x_n は 0 へ収束する。この収束先の x_n = 0 という点は、式 (2-3) で示した不動点 x_f 1 である。このように周りの軌道が収束するタイプの不動点は、漸近安定、安定、あるいは吸引的と呼ばれる。逆に時間 n の増加と共に x_f の近くの軌道が x_f から離れていくならば、その不動点 x_f は不安定や反発的と呼ばれる。

パラメータ a = 0.9 のクモの巣図（左）と時系列（n と x_n の関係）の図（右）。軌道は 0 に向かって単調減少で収束する。

不動点が漸近安定かどうかを知るには、写像 f の微分を求めるという一般的で簡単な方法がある。f (x) の微分 df (x)/dx を f ′(x) と表すとする。 この微分が不動点 x_f で

$\left|f'(x_{f})\right|<1$

(3-1)

という条件を満たせば、x_f は漸近安定である。ここで、|〇| は 〇 の絶対値を意味する。

漸近安定な不動点（左）と不安定な不動点（右）の接線傾きと周囲の軌道の様子

写像のグラフでこのことを見ると、グラフの曲線上の点 x_f における接線の傾きが −1 から 1 の間にあれば、x_f は安定で、その周囲の軌道は x_f へ引き寄せられるということである。ロジスティック写像の微分は、

$f'(x)=a(1-2x)$

(3-2)

なので、x = 0 かつ 0 < a < 1 では 0 < f ′(0) < 1 であるから、不動点 x_f 1 = 0 は式 (3-1) を満たしている。

ただし、式 (3-1) による判別法は、x_f からどのぐらいの範囲にある軌道が x_f へ引き寄せられるかは分からない。あくまでも、x_f のある近傍内の x が収束することを保証しているだけである。今の場合、0 へ収束する初期値の領域は [0, 1] 全域であるが、これを明確に知るには別の考察を要する。

不動点が不安定かどうかの判別方法は、同じように写像の微分から分かる。ある不動点 x_f が

$\left|f'(x_{f})\right|>1$

(3-3)

を満たすとき、x_f は不安定である。パラメータが 0 < a < 1 の範囲にあるときには、もう一方の不動点 x_f 2 = 1 − 1/a は負の値であるため [0, 1] の範囲には現れないが、不安定な不動点として存在している。

1 ≤ a ≤ 2 のとき

パラメータがちょうど a = 1 のとき、ロジスティック写像の軌道はこれまでと同様に 0 へ収束する。ただし、収束する速さが、a = 1 ではゆっくりになる。a = 1 における不動点 0 は漸近安定ではあるが、式 (3-1) を満たしていない。実のところ、式 (3-1) による判別法は写像を不動点近傍で1次近似することによって成り立っている。a = 1 ではこの近似が成り立たなくなり、安定・不安定は写像の2次（2乗）の項によって決まるようになる。

a = 1 の状態をグラフで見ると、x = 0 でグラフの曲線が45°対角線にちょうど接した状態になっている。このとき、0 < a < 1 の範囲では負の範囲に存在していた不動点 x_f 2 = 1 − 1/a の値は、x_f 2 = 0 となっている。つまり、a が増えるにつれて x_f 2 の値は 0 へと近づいていき、ちょうど a = 1 で、x_f 2 は x_f 1 = 0 と衝突する。この衝突によってトランスクリティカル分岐という現象が起こる。

a = 1 で起こるロジスティック写像のトランスクリティカル分岐の様子。a < 1 では x_f 2 が不安定な不動点として [0, 1] の外に存在しているが、a = 1 で2つの不動点が衝突し、a > 1 では x_f 2 が安定な不動点として [0, 1] の間に現れる。

分岐とは力学系の振る舞いが定性的に変わる現象を指す用語で、この場合のトランスクリティカル分岐では、不動点同士で安定性の交替が起きる。つまり、a が 1 未満では x_f 1 は安定、x_f 2 は不安定であたったが、a が 1 を超えると x_f 1 は不安定、x_f 2 は安定になる。分岐が起きるときのパラメータの値は分岐点と呼ばれる。ここでは、a = 1 が分岐点である。

分岐の結果、ロジスティック写像の軌道は x_f 1 = 0 ではなく、x_f 2 = 1 − 1/a へ収束するようになる。詳しく言えば、パラメータ 1 < a ≤ 2 であれば、0 と 1 を除く区間 (0, 1) 上の値から出発する軌道は、単調増加あるいは単調減少しながら x_f 2 に収束する。収束の仕方の違いは、初期値がどの範囲にあるかに依る。0 < x₀ < 1 − 1/a では単調増加で収束し、1 − 1/a < x₀ < 1/a では単調減少で収束し、1/a < x₀ < 1 では最初の1ステップを除いて単調増加で収束する。

不動点 x_f 2 = 1 − 1/a に単調減少で収束する例（a = 1.2、x₀ = 0.6）

不動点 x_f 2 = 1 − 1/a に単調増加で収束する例（a = 1.8、x₀ = 0.2）

また、分岐によって不動点 x_f 1 = 0 は不安定化するが、a > 1 以降も不動点として存在し続ける。この不安定不動点 x_f 1 にたどり着く初期値が、x_f 1 自身以外に存在しないわけではない。それが x₀ = 1 で、a の値にかかわらずロジスティック写像は f (1) = 0 を満たすので、x₀ = 1 に写像を1回適用すると x_f 1 = 0 に写る。この x = 1 のように、有限回の写像の反復で不動点に直接行き着くような点は最終的不動点などと呼ばれる。

2 < a < 3 のとき

a = 2.8 におけるクモの巣図法のアニメーション。不動点の周りを回りながら収束していく。

パラメータが 2 < a < 3 のときは、初期値 0 と 1 を除いて、1 < a ≤ 2 のときと同様に不動点 x_f 2 = 1 − 1/a に収束する。ただし、この場合は単調に収束するわけではない。変数が x_f 2 にある程度近づくと、変数は x_f 2 よりも大きくなったり小さくなったりを繰り返し、x_f 2 の周りで振動しながら収束していくような軌道を示す。

軌道の不動点周りでの振動は、次のような範囲を行き来する。このパラメータ範囲では、x_f 2 は区間 (1/2, 1) 内に存在する。写像を一回適用すると x_f 2 に写る値を ~x_f 2 と表記するとする。すなわち、f (~x_f 2) = x_f 2 という関係である。変数が区間 (~x_f 2, x_f 2) に入ったとき、軌道の不動点周りでの振動が起こり出す。(~x_f 2, x_f 2) は (x_f 2, a/4] へ写され、 (x_f 2, a/4] は [1/2, x_f 2) の中へ写され、…といった具合に振動する。

一般的に、分岐の様子を理解するのには分岐図が役に立つ。この図は不動点（または後述の周期点）x をパラメータ a の関数として表したグラフで、横軸に a の値を取り、縦軸に x の値を取って図示する。 安定な不動点と不安定な不動点を区別するために、前者の曲線は実線で示し、後者の曲線は点線で示したりする。ロジスティック写像の分岐図を書くと、不動点 x_f 1 = 0 を表す直線と不動点 x_f 2 = 1 − 1/a を表す曲線が a = 1 で交わり、安定性が入れ替わる様子がわかる。

パラメータ 0 から 3 までのロジスティック写像の分岐図。青線が不動点 x_f 1 = 0 を表し、赤線が不動点 x_f 2 = 1 − 1/a を表す。

3 ≤ a < 3.44949… のとき

パラメータがちょうど a = 3 のときも、軌道は不動点 x_f 2 = 1 − 1/a に収束する。しかし、2 < a < 3 のときよりも変数が収束する速さは遅い。a = 3 では、微分係数 f ′(x_f 2) は −1 に達し、式 (3-1) を満たさなくなっている。a が 3 を過ぎると、f ′(x_f 2) < −1 となり、x_f 2 は不安定な不動点になる。すなわち、a = 3 でまた分岐が起こる。

a = 3 では、周期倍化分岐と呼ばれる種類の分岐が起こる。a > 3 からは、軌道は1点に収束しなくなり、十分に時間 n が進んだ後でも大きい値と小さい値を交互に取り続けるような振る舞いに変わる。例えば a = 3.3 であれば、変数は 0.4794… と 0.8236… という2つの値を交互に取り続ける。

a = 3.3 のときのクモの巣図と時系列。軌道は安定な2周期点に吸引される。

このように同じ値を周期的に巡り続ける軌道を周期軌道と呼ぶ。今の場合、n → ∞ における変数の最終的な振る舞いは2周期の周期軌道である。周期軌道を構成する一つ一つの値（点）を周期点と呼ぶ。a = 3.3 の例で言えば、0.4794… と 0.8236… がそれぞれ周期点である。ある x が周期点だとすると、2周期点の場合は x に写像を2回適用すると元に戻るので、

$f^{2}(x)=x$

(3-4)

という関係が成り立つ。この式にロジスティック写像の式 (1-4) を適用すると、

$a^{2}x(1-x)(1-ax(1-x))=x$

(3-5)

という4次方程式が得られる。この方程式の解が周期点である。実は不動点 x_f 1 = 0 と不動点 x_f 2 = 1 − 1/a もまた、式 (3-4) を満たす。したがって、式 (3-5) の解の内、2つの解は x_f 1 と x_f 2 に相当し、残り2つの解が2周期点である。2周期点をそれぞれ x⁽²⁾_f 1, x⁽²⁾_f 2 と表すとする。式 (3-5) を解くことで、x⁽²⁾_f 1, x⁽²⁾_f 2 を次のように得られる。

$x_{f1}^{(2)},\ x_{f2}^{(2)}={\frac {a+1\pm {\sqrt {(a+1)(a-3)}}}{2a}}$

(3-6)

不動点の安定性と同じようなことが、周期点についても言える。つまり、周囲の軌道を引き付ける周期点は漸近安定な周期点と呼ばれ、周囲の軌道が離れていく周期点は不安定な周期点と呼ばれる。周期点の安定性判別も、不動点と同じように可能である。一般的な場合を想定して、写像を k 回反復させた f ^k(x) について考える。この微分 df ^k(x)/dx を (f ^k)′(x) と表すとする。ある k-周期点 x^(k)_f が

$\left|(f^{k})'(x_{f}^{(k)})\right|<1$

(3-7)

を満たせば、x^(k)_f は漸近安定である。不安定についても不動点と同じように

$\left|(f^{k})'(x_{f}^{(k)})\right|>1$

(3-8)

を満たせば、x^(k)_f は不安定である。

以上の周期点の安定性の議論も、不動点と同じようにグラフ描写によって理解しやすくなる。この図では、横軸 x_n に対して縦軸を x_n+2 とし、x_n+2 と x_n の関係を表す曲線を描く。この曲線と45°直線の交点は式 (3-4) を満たす点であるから、交点は不動点と2周期点を表している。ロジスティック写像の f ²(x) のグラフを描くと、不動点 x_f 2 での接線の傾きは a = 3 を境に 1 を超えて不安定化するのが観察できる。同時に新たな2つの交点が現れ、これらが周期点 x⁽²⁾_f 1 と x⁽²⁾_f 2 である。

a = 2.7 のときの x_n+2 と x_n の関係。周期倍化分岐が起こる前。軌道は不動点 x_f 2 に収束する。

a = 3 のときの x_n+2 と x_n の関係。不動点 x_f 2 での接線傾きはちょうど 1 となり、周期倍化分岐が起こる。

a = 3.3 のときの x_n+2 と x_n の関係。x_f 2 は不安定化し、軌道は周期点 x⁽²⁾_f 1 と x⁽²⁾_f 2 に収束する。

2周期点の微分係数をロジスティック写像について実際に計算すると、

$(f^{2})'(x_{f}^{(2)})=4+2a-a^{2}$

(3-9)

となる。これを式 (3-7) に当てはめると、パラメータ a が、

$\left|4+2a-a^{2}\right|<1$

(3-10)

を満たすときに2周期点が漸近安定であることがわかる。この範囲は 3 < a < 1 + √6 となり、つまり a が 1 + √6 = 3.44949… を超えると、2周期点は漸近安定ではなくなり、また振る舞いが変わる。

[0, 1] 内のほぼ全ての初期値が2周期点に引き寄せられるが、 x_f 1 = 0 と x_f 2 = 1 − 1/a も [0, 1] 内に不安定な不動点として残り続けている。これら不安定不動点は、以後 a を増やし続けても [0, 1] 内にずっと残り続ける。そのため、初期値がちょうど x_f 1 または x_f 2 であるときは、軌道は2周期点には引き寄せられない。さらに、初期値が x_f 1 に対する最終的不動点である場合と、x_f 2 に対する最終的不動点である場合も、軌道は2周期点には引き寄せられない。このような最終的不動点である点は [0, 1] の中に無限に存在する。しかし、このような点の数は、[0, 1] という実数の集合と比較すれば無視できるほど小さい。

3.44949… ≤ a ≤ 3.56994… のとき

パラメータ a が 1 + √6 = 3.44949… を超えると、それまで安定だった2周期点が不安定になり、安定な4周期点が新たに生まれ、軌道は4周期の振動に引き寄せられるようになる。つまり、a = 3.44949… でまた周期倍化分岐が起こる。4周期点における x の値も

$f^{4}(x)=x$

(3-11)

を満たすので、この式を解けば4周期点の x の値を求めることができる。ただし、式 (3-11) は16次方程式であり、不動点と2周期点の4つの解をくくり出したとしても12次方程式である。そのため、もはやこれを解いて、2周期点と同じように4周期点の値を表す a の陽関数を得ることはできない。

256周期までの分岐点の例

k 番目の分岐	周期 2k	分岐点 ak
1	2	3.0000000
2	4	3.4494896
3	8	3.5440903
4	16	3.5644073
5	32	3.5687594
6	64	3.5696916
7	128	3.5698913
8	256	3.5699340

さらに a が大きくなると、安定な4周期点はまた周期倍化分岐を起こし、安定な8周期点が生まれる。以降、a が増えるにつれて、16周期、32周期、64周期、…と周期倍化分岐が無限に起こり続け、最終的には無限周期すなわち永遠に元の値に戻ることがない軌道となる。この周期倍化分岐の無限の系列はカスケードと呼ばれる。この周期倍化分岐は無限に起こるが、一方で、周期倍化分岐が発生する a の間隔は等比数列的に減少していく。そのため、パラメータ a がある有限の値に達するまでに、周期倍化分岐の無限回の発生が起きる。a = 3 で起きた1周期から2周期への分岐を1番目の周期倍化分岐として数えるとする。すると、この周期倍化分岐のカスケードの中では、k 番目の分岐点で安定な 2^k 周期点が発生する。k 番目の分岐点 a を a_k と表すとする。このとき、k → ∞ で a_k は次のような値に収束することが知られている。

$a_{\infty }=\lim _{k\rightarrow \infty }a_{k}=3.56994\cdots$

(3-12)

さらに、a_k の減少の割合の極限は次式で示すような定数値となることが知られている。

$\delta =\lim _{k\to \infty }{\frac {a_{k}-a_{k-1}}{a_{k+1}-a_{k}}}=4.66920\cdots$

(3-13)

この δ の値は、数理物理学者のミッチェル・ファイゲンバウムにより発見されたことからファイゲンバウム定数と呼ばれる。a_∞ はファイゲンバウム点と呼ばれる。周期倍化カスケードの過程では、f ^m と f ^2m は適当なスケール変換によって局所的に全く一致する性質を持つ。この自己相似性を利用した繰り込みと呼ばれる手法により、ファイゲンバウム定数は求められる。以上のようなロジスティック写像が周期倍化カスケードの過程で見せる性質は、後述のように、より広いクラスの写像でも普遍的に現れる。

あるパラメータに対して軌道が落ち着く最終的な振る舞いを一望するには、近似的な分岐図である軌道図が有用である。この図では、分岐図と同じように横軸にパラメータ a を取り、縦軸に変数 x を取る。コンピュータなどを使い、パラメータを決めて、例えば500回反復計算を行う。そして、計算結果の最初の100回を無視して残りの400回の結果のみを図示する。これによって、初期の過渡的な振る舞いは無視でき、軌道の漸近的な挙動が残る。例えば、ある a に対して1点プロットされるときは、それは不動点であり、ある a に対して m 点プロットされるときは、それは m 周期軌道に相当する。ロジスティック写像に対して軌道図を書くと、安定な周期軌道を表す枝が分裂していく様子が見て取れ、これが周期倍化分岐のカスケードを表している。

パラメータ a₁ = 3 から a_∞ = 3.56994… の間で起こる周期倍分岐カスケードの軌道図。64周期（a₅）以降は間隔が非常に狭くなり、ほとんどつぶれている。

パラメータがちょうど周期倍化カスケードの集積点 a = a_∞ であるとき、変数 x_n は永遠に閉じることのない非周期軌道へ引き付けられる。言い換えると、a_∞ では無限周期の周期点が存在している。この非周期軌道はファイゲンバウム・アトラクタや臨界2^∞アトラクタと呼ばれる。アトラクタとは、周りの軌道を引き付けるような性質をもった領域を指す用語で、引き込まれて最終的に続く軌道のことである。これまで述べてきた吸引的な不動点や周期点もアトラクタの仲間である。

ファイゲンバウム・アトラクタの構造は、カントール集合というフラクタル図形と同じ構造になっている。ファイゲンバウム・アトラクタを構成する点は、無限個でなおかつその濃度は実数と等しい。一方で、構成する点のどの2つを選んでも、その間に不安定な周期点が必ず存在し、点の分布は連続ではない。また、ファイゲンバウム・アトラクタのフラクタル次元は、ハウスドルフ次元あるいは容量次元でおよそ 0.54 であることが知られている。

カントール集合の構成例。線分の真ん中3分の1を無限に除去し続けると、長さは 0 で何も残らないように見えて、点の数は非可算無限で、それぞれの点のどれだけ小さい近傍の中にも他の点が無限に含まれる、という図形ができる。

3.56994… < a < 4 のとき

カオスの出現

a = 3.82のときのロジスティック写像のカオス軌道。オレンジ四角が x₀ = 0.1234 から出発する軌道で、青緑丸が ˆx₀ = 0.1234 + 10⁻⁹ から出発する軌道。

x₀ = 0.1234 から出発する軌道と ˆx₀ = 0.1234 + 10⁻⁹ から出発する軌道の差が、指数関数的に成長する様子。縦軸は Δx_n = |x_n − ˆx_n| で、対数スケールで表示している。

パラメータ a が a_∞ = 3.56994… を超えると、ロジスティック写像はカオスと呼ばれる振る舞いを示す。カオスとは、大雑把に言えば、ロジスティック写像を表す差分方程式のように確率的な曖昧さがなく次の状態が完全に一意に決まるにもかかわらず起こる複雑で不規則な振る舞いのことである。ロジスティック写像の a > a_∞ の範囲はカオス領域と呼ばれる。

カオスが持つ本質の一つが、バタフライ効果という言葉で象徴される予測不可能性である。これは、カオスによって初期の状態のわずかな違いが後の状態に巨大な差をもたらすという性質に起因する。離散力学系で言えば、2つの初期値 x₀ と ˆx₀ がどれだけ近い値だとしても、時間 n がある程度進めば、それぞれの行先 x_n と ˆx_n は著しく離れてしまう。例えば a = 3.95 を使い、x₀ = 0.1 と ˆx₀ = 0.1000000001 というきわめて近い2つの初期値でそれぞれの軌道を計算すると、その差は、反復29回を過ぎたころから図上ではっきりわかるほど巨視的な違いに成長する。

以上のような初期値鋭敏性と呼ばれるカオスの性質は、リアプノフ指数によって定量的に表される。1次元写像の場合、リアプノフ指数 λ は次のように計算できる。

$\lambda =\lim _{N\to \infty }{\frac {1}{N}}\sum _{i=0}^{N-1}\log \left|f^{\prime }(x_{i})\right\vert$

(3-14)

ここで、log は自然対数を意味する。この λ は2つの軌道の距離（x_n と ˆx_n の距離）が指数関数的にどのぐらいの速さで離れていくか意味する指標で、λ の値が正ならば初期値鋭敏性を持つ系であること意味し、零または負ならば初期値鋭敏性のないことを意味する。実際にロジスティック写像の λ を数値的に計算すると、a < a_∞ の範囲では λ は零または負の値の範囲に留まっており、a > a_∞ の範囲から λ が正の値も取るようになることが確認できる。

窓、間欠性

パラメータが a_∞ を超えてからも、振る舞いのパラメータ a への依存の仕方は単純ではない。a > a_∞ のカオス領域には、多くの精巧な数学的構造が潜んでいる。この領域では、ずっとカオスが続くというわけではなく、安定な周期軌道も再び現れる。a_∞ < a ≤ 4 での振る舞いは、大きく分けると以下の2種類に分かれる。

• 安定な周期点。この場合、リアプノフ指数は負を示す。
• 非周期的軌道。この場合、リアプノフ指数は正を示す。

a_∞ < a ≤ 4 の中に存在する安定周期点の領域は周期窓あるいは単に窓と呼ばれる。カオス領域を軌道図で見ると、非周期的軌道の領域は無数の点でできた雲のような見た目を示し、その雲に囲まれて点在する空白部分が窓である。

a = 3.55 から a = 4 までのロジスティック写像の軌道図（図中では パラメータが r 表記）

各窓では、a_∞ = 3.56994… よりも前で起きた周期倍化分岐のカスケードが再び起きる。ただし、それらの周期は前のような 2^k の安定周期軌道ではなく、3×2^k や 5×2^k のような新しい安定周期軌道が生成される。最初は p 周期で、そこから周期倍化カスケードが起こる窓は周期 p の窓などと呼ばれる。例えば、周期3の窓は 3.8284 < a < 3.8415 辺りの領域に存在しており、この領域内では 3, 6, 12, 24, …, 3×2^k, … という風に周期が倍化していく。

a = 3.8285 で起きる過渡カオスの様子。3周期軌道に吸引されるまでカオス的に振る舞う。

窓の領域では、カオスは消えておらず背後に存在している。しかし、このカオスは不安定であるため、安定な周期軌道のみが観測される。窓の領域では、軌道が初期値から安定周期軌道に吸引されるまでに、この潜在的なカオスが現れる。このようなカオスを過渡カオスと呼ぶ。このようにカオスが潜在的に存在している点において、窓は a_∞ より前で現れた周期軌道とは異なる。

窓の数は、a_∞ < a < 4 の範囲に無限個ある。それらの窓の周期は様々で、3 以上の全ての自然数に対応する周期の窓が存在する。しかし、各周期の窓がそれぞれ1回ずつ発生するわけではない。p の値が大きいほどその周期の窓は多く繰り返し発生する。周期3の窓は1回きりで、例えば周期13の窓は315 回発生する。その周期3の窓で3周期軌道が生じるとシャルコフスキー順序が完成し、全ての周期の軌道がそれで一通り出現し終える。

p が素数の場合に限定すると、周期 p の窓の個数は

$N_{p}={\frac {2^{p-1}-1}{p}}$

(3-15)

という式で計算できる。この式は p を素数に限定して導出されたものだが、実際のところ、素数でない p の安定 p 周期点の数についても良い精度で計算できる。

窓の幅（窓が始まる a と窓が終わる a の差）は、周期3の窓が最も広く、周期が大きいほど幅は狭まっていく。例えば、周期13の窓の幅は 3.13 × 10⁻⁶ 程度である。概算によると、[a_∞, 4] の内のおよそ 10% が窓の領域で、残りがカオス軌道が支配する領域となっている。

a を増やしていくときに起こるカオスから窓への変化は、接線分岐と呼ばれる分岐によって引き起こされる。これは、写像の曲線が y = x の対角線に分岐の瞬間にちょうど接し、さらにパラメータを変化させると曲線と直線が交わって2つの不動点を持つようになる分岐である。周期 p の窓であれば、反復写像 f ^p(x) が接線分岐を起こすことによって安定な p 周期軌道が生まれる。周期3の窓の接線分岐については正確な分岐点の値が知られており、この分岐点 a の値を a₃ とすると、a₃ = 1 + √8 = 3.828427… である。この分岐の概要は、f ³(x) のグラフ（縦軸 x_n+3・横軸 x_n のグラフ）を考察することで理解できる。

a₃ よりもわずかに小さいときの f ³(x) のグラフ。グラフは不動点以外では接しておらず、3周期点が存在しない。

a₃ ちょうどのとき。グラフは3点で対角線にちょうど接し、3周期点が生まれる。

a₃ よりもわずかに大きいとき。グラフは対角線を通り過ぎ、安定な3周期点と不安定な3周期点に分かれる。

この分岐点 a₃ よりもわずかに小さい a = 3.8282 のときの x_n 振る舞いを見てみると、不規則変化に加えて、ほぼ3周期で周期的変化する振る舞いも存在しており、これらが交互に発生する様子が確認される。このような周期的振る舞い部分はラミナーと呼ばれ、不規則振る舞い部分はバーストと呼ばれる。バーストとラミナーの時間帯の長さに規則性は無く、不規則に変化する。しかし、より a₃ に近い a = 3.828327 という値で振る舞いを観察すると、a = 3.8282 のときよりラミナーの平均的な時間長さが長くなり、バーストの平均的な時間長さが短くなる。さらに a を大きくしていくとラミナーの長さがどんどん大きくなっていき、a₃ に至ったところで完全な3周期に変わる。

a = 3.8282 のときの時系列

a = 3.828327 のときの時系列

a₃ = 3.828427… 直前で起きる間欠性の様子。周期的にほぼ同じ3つの値が続いている部分がラミナー、カオス的な不規則変化を起こしている部分がバースト。

このように、ラミナーという秩序的な運動とバーストという乱れた運動が間欠的に繰り返し起こる現象は、間欠性や間欠性カオスと呼ばれる。パラメータ a を逆に a₃ から小さくする方向で考えてみると、これはカオスの発生の一種となっている。パラメータが窓から離れる方向へ動くほど、バーストが支配的になっていき、最終的には完全なカオス状態となる。これも前述の周期倍分岐ルートと同じくカオスに至る一般的な道筋の一種で、このような接線分岐による間欠カオスの発生を特徴とした道筋は間欠性ルートと呼ばれる。

f ³(x) のグラフで現れるチャネルの様子

間欠性の発生メカニズムもまた、写像のグラフから理解することができる。a が a₃ よりもわずかに小さいとき、f ³(x) のグラフと対角線の間にはとても小さい隙間が存在する。この隙間はチャネルと呼ばれ、狭いチャネルを軌道が通過するために多数の写像の反復が起こる。このチャネルを通り過ぎる過程では x_n と x_n+3 はとても近い値になり、実質的にほとんど3周期軌道のように変数が変化する。これがラミナーに相当する。軌道はやがてこの細いチャネルを抜けるが、写像の大域的な構造の結果、ふたたびチャネルに戻って来る。チャネルを離れている間はカオス的な乱れた動きをする。これがバーストに相当する。

バンド、窓の終わり

カオス領域の全体に目を移すと、カオスであっても窓であっても、軌道図の縦軸の最大値と最小値（アトラクタの上限値と下限値）はある範囲内に限られている。式 (2-1) が示すようにロジスティック写像の最大値は a/4 で与えられ、これがアトラクタの上限値となる。アトラクタの下限値は、a/4 が写る点 f (a/4) で与えられる。結局、軌道図で x_n が動く最大値と最小値は、パラメータ a に依存して

${\frac {a^{2}(4-a)}{16}}\leq x_{n}\leq {\frac {a}{4}}$

(3-16)

と与えられる。最終的には、a = 4 で軌道は [0, 1] 全体に及ぶ。

軌道図を観察すると、点の分布に特徴的な濃淡が見られる。点が濃い部分は、変数がその周辺の値を取る頻度が大きいことを意味しており、点が薄い部分は、変数がその周辺の値を取る頻度が小さいことを意味している。このような点が訪れる頻度の差異は、ロジスティック写像のグラフの形に起因して生まれる。グラフの最頂部 a/4 近辺が高頻度で軌道を呼び込み、そこから写された先の f (a/4) 近辺も高頻度になり、そこから写された先の f ²(a/4) 近辺も高頻度になり…、という具合に頻度の分布が生まれる。写像によって生まれる点の密度分布は不変測度や分布関数と呼ばれる量で特徴づけられ、アトラクタの不変測度は初期値に関わらず再現性がある。

軌道図カオス領域の初めの辺り、 a が最初の2周期倍化カスケードの集積点 a_∞ = 3.56994… を少し超えた辺りを見てみると、軌道がいくつかの区間に分かれていることが観察できる。このように分かれた小領域はバンドと呼ばれる。バンドが複数ある場合、軌道は規則的に順番に各バンドを巡り、なおかつ各バンド内での取る値は不規則的となるような振る舞いを示す。このようなカオス軌道はバンドカオスや周期的カオスと呼ばれ、k 個のバンドから成るカオスは k バンドカオスなどと呼ばれる。2バンドカオスであれば、およそ 3.590 < a < 3.675 の範囲内に存在している。

バンド構造の様子。e_p の間隔が急激に小さくなっていくため、8バンド以上は図示できていない。軌道が収まっている最上部と最下部の線が式 (3-16) の範囲内にある。

2バンドカオスの左端 a = 3.590 からさらに値を小さくしていくと、周期倍加分岐のときと同じようにバンドの数が2倍ずつ増えていく。p−1 バンドカオスが分裂して p バンドカオスになる分岐点、あるいは p バンドカオスが融合して p−1 バンドカオスになる分岐点を e_p (ただし p = 1, 2, 4, …, 2^k, …）で表すとする。すると、周期倍加分岐と同じように p → ∞ で e_p はある値に集積する。この集積点 e_∞ でバンドの数は無限となり、e_∞ の値は a_∞ の値と一致する。

ロジスティック写像の軌道図全体の自己相似階層構造

a_∞ より前に現れた周期倍化分岐カスケードの分岐点についても、同じように、p 安定周期軌道が分岐して p+1 安定周期軌道になる分岐点を a_p（ただし p = 1, 2, 4, …, 2^k, …）で表すとする。このとき、a₂ から e₂ までの軌道図に着目すると、a₁ から e₁ までの全体軌道図の縮小版が a₂ から e₂ までの軌道図の中に2つ存在している。同様に、a₄ から e₄ までの軌道図に着目すると、a₁ から e₁ までの全体軌道図の縮小版が a₄ から e₄ までの軌道図の中に4つ存在している。以下同様に a_p から e_p までの軌道図には全体軌道図の縮小版が p 個存在しており、ロジスティック写像の分岐構造は無限の自己相似階層を備えている。

ロジスティック写像の窓の自己相似階層構造

分岐構造の自己相似階層は、窓の中にも存在する。窓の中の周期倍化分岐カスケードは、2^k 周期分岐のカスケードと同じ筋道をたどる。つまり、窓の中で無限回の周期倍化分岐が起き、それを過ぎると振る舞いはまたカオスとなる。例えば周期3の窓では、a_3∞ ≈ 3.8495 で安定な周期軌道のカスケードが終わる。a_3∞ ≈ 3.8495 を過ぎると、振る舞いは3の倍数のバンドカオスになる。a が a_3∞ から増えるにつれて、このバンドカオスも2個ずつ融合していき、窓が終わる最後にはバンドの数は3つになる。このような窓の中にあるバンドの中にも、無数の窓がまたさらに存在している。結局、窓の中には 1 ≤ a ≤ 4 の軌道図全体の縮小版が含まれているような恰好となり、窓の中にも分岐の自己相似階層構造が存在している。

窓が終わると、広範囲のカオスに戻る。周期3の窓であれば、a ≈ 3.857 で最後の3バンドカオスが大きな範囲の1バンドカオスへ変わって窓が終わる。しかし、この変化は非連続的で、3バンドのカオスアトラクタは突然大きさを変化させ、1バンドへ変わる。このようにアトラクタの大きさが非連続的に変わる現象は、クライシスと呼ばれる。窓の終わりで起きるような種類のクライシスは、特に内部クライシスとも呼ばれる。窓の終わりでクライシスが起きるとき、安定な周期軌道が軌道図上では見えない不安定周期点とちょうど接触する。これによって周期軌道が逃げ出せる出口が生まれ、内部クライシスが発生する。内部クライシス直後には、ある時間帯では広域のカオスとして振る舞うが、ある時間帯では元のバンドカオス的振る舞いも起こし、窓の始まりと同じような一種の間欠性が現れる。

a = 4 のとき

パラメータ a = 4 のロジスティック写像のクモの巣図（左）と、n = 500までの時系列図（右）。初期値 x₀ = 0.3 の場合。

パラメータが a = 4 に達すると、振る舞いは [0, 1] 全域を経巡るカオスとなる。このとき、リアプノフ指数 λ は最大となり、もっともカオスが強い状態といえる。a = 4 におけるロジスティック写像の λ は正確な値を求ることができ、その値は λ = log 2 である。カオスの厳密な数学的定義はまだ統一されていないが、よく知られているカオスの定義の一つに対して a = 4 のロジスティック写像は [0, 1] 上でカオス的であることが証明できる。

a = 4 のときの不変測度 ρ (x) のグラフ。点プロットは、（高さを ρ (x) に合わせた）10000回反復で得られた実際の点の頻度を示す。

点の密度の不変測度 ρ (x) も、a = 4 のときは次のような正確な関数で与えることができる。

$\rho (x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}$

(3-17)

ここで ρ (x) は、写像を反復したときの点 x_n の全点数に対し、点 x_n が微小区間 [x, x+dx] に入る点数の割合が、ρ (x)dx で与えられるという意味を持つ。a = 4 のロジスティック写像の頻度分布は、[0, 1] の両サイド近辺で密度が高く、x = 0.5 で最も密度が低い形をしている。

a = 4 のとき、カオス軌道とは別に、あらゆる周期の周期軌道も存在している。自然数 n に対して、f_a=4ⁿ(x) のグラフは 2ⁿ⁻¹ 個の山と 2ⁿ⁻¹ − 1 個の谷が存在する曲線となり、しかもそれら全ての山と谷は 0 と 1 に接する状態になる。したがって、対角線とグラフの交点の数は 2ⁿ 個あり、f ⁿ(x) の不動点は 2ⁿ 個存在する。この 2ⁿ 個の不動点には n 周期点も必ず含まれているので、f_a=4 ⁿ(x) では任意のn 周期軌道が存在する。このように、a = 4 のとき [0, 1] 上には周期点が無限に存在しているが、それら周期点は全て不安定である。また、区間 [0, 1] という非可算無限の集合に対してそれら周期点の数は可算無限であり、ほとんど全ての初期値から始まる軌道は周期軌道とはならずに非周期軌道となる。

ロジスティック写像 f_a=4 の軌道を 0 と 1 の記号列に変換すると、あらゆる記号列が再現できる

カオスの重要性の一つに、決定論的性質と確率論的性質の二重性がある。力学系は決定論的な過程だが、変数が取る範囲を適当に粗視化すると確率的な過程と区別ができなくなる。a = 4 のロジスティック写像の場合であれば、あらゆるコイン投げの結果をロジスティック写像の軌道で記述できる。このことを詳述すると次のとおりである。

1/2 の確率で表裏が出るコイン投げを想定し、何回もコイン投げを続ける。表が出たときを 0、裏が出たときを 1 とすれば、表裏表表裏…という結果は 01001… といったような記号列になる。一方で、ロジスティック写像の軌道 x₀, x₁, x₂,… について、x = 0.5 以下のものは 0 に x = 0.5 を超えるものは 1 に変換し、軌道を 0 と 1 から成る記号列に置き換える。例えば、初期値 x₀ = 0.2 とすれば、 x₁ = 0.64, x₂ = 0.9216, x₃ = 0.28901, … となるので、軌道は 0110… という記号列になる。前者のコイン投げによる記号列を S_C とし、後者のロジスティック写像による記号列を S_L とする。記号列 S_C には、ランダムなコイン投げで記号を決めていったのであらゆるパターンの数列があり得る。よって、ロジスティック写像による記号列 S_L がどんなものだったとしても、S_C の中に同一のものが存在する。そして、「実に驚くべきこと」として、この逆が成立する。つまり、どのような S_C の記号列であっても、初期値を適切に選びさえすればロジスティック写像の軌道 S_L によって実現できる。すなわち、任意の S_C に対し、S_C = S_L となる x₀ が [0, 1] 中にただ1点存在する。

a > 4 のとき

a = 4.5 のロジスティック写像では、[0, 1] のほとんどの全ての点から出発する軌道はマイナス無限大へ向かう

パラメータ a が 4 を超えると、ロジスティック写像のグラフの頂点 a/4 は 1 を超える。グラフが 1 を突き抜けている範囲から、軌道は [0, 1] を抜け出せるようになる。その結果、[0, 1] のほとんどの全ての点から出発する軌道はどこかの時点で [0, 1] を抜け出し、最終的にマイナス無限大へ発散してしまう。

この a = 4 で起こる分岐もクライシスの一種で、とくに境界クライシスと呼ばれる。この場合の境界クライシスでは、[0, 1] にあったアトラクタが不安定化・崩壊し、なおかつ外側にアトラクタも存在しないため、軌道が無限遠へと発散してしまう。

一方で、a > 4 の条件下でも [0, 1] の中に留まり続ける軌道がある。分かりやすい例は [0, 1] 内の不動点や周期点で、これらは [0, 1] の中に留まり続ける。しかし、[0, 1] の中に留まり続ける軌道には、不動点や周期点以外の軌道も存在している。

f (x) > 1 を満たす x の区間を A₀ とする。上記の通り、変数 x_n が A₀ に一旦入ると、マイナス無限大へ発散する。写像を1回適用すると A₀ へ写る x も [0, 1] の中に存在している。この x の区間は2つに分かれており、それらをまとめて A₁ とする。同じように、写像を1回適用すると A₁ へ写る区間も4つ存在し、それらを A₂ とする。以下同じように、n 回反復で A₀ にたどり着く区間 A_n が 2ⁿ 個存在する。 したがって、次のように [0, 1] から A_n を無限回取り除いた区間 Λ が、I の中に留まり続ける軌道の集まりである。

$\Lambda =\left[0,\ 1\right]-\bigcup _{n=0}^{\infty }A_{n}$

(3-18)

[0, 1] から A_n を取り除いていく作業は上述のカントール集合の構成過程に似ており、実際に Λ はカントール集合（閉で完全不連結で[0, 1] の完全部分集合）の形で [0, 1] の中に存在している。そしてさらに、Λ 上でロジスティック写像 f_a>4 はカオス的である。

a < 0 のとき

ロジスティック写像は生態学上のモデルとして研究された経緯もあり、パラメータ a が負の場合について論じられることは少ない。a を 0 から減少させていくと、−1 < a < 0 では x_f = 0 の安定不動点に漸近するが、a = −1 を超えたところから2周期点に分岐し、正のときと同じく周期倍化分岐を経てカオスへ至る。最終的には、a = −2 を下回るとプラス無限大へ発散するようになる。

パラメータ a が −2 から 4 までの軌道図。負側も正側もこれらのパラメータ範囲を超えると発散する。

特別な場合の厳密解

パラメータ a が特定のロジスティック写像については、時刻 n と初期値 x₀ を陽に含む厳密解が以下のように得られている。

a = 4 のとき

$x_{n}={\frac {1-\cos \left[2^{n}\arccos(1-2x_{0})\right]}{2}}$

(3-19)

a = 2 のとき

$x_{n}={\frac {1-\exp \left[2^{n}\log(1-2x_{0})\right]}{2}}$

(3-20)

a = −2 のとき

$x_{n}={\frac {1}{2}}-\cos \left\{{\frac {1}{3}}\left[\pi -(-2)^{n}\left(\pi -3\arccos({\frac {1}{2}}-x_{0})\right)\right]\right\}$

(3-21)

以上3つの厳密解を考察すると、いずれの解も

$x_{n}={\frac {1}{2}}\left\{1-f\left[a^{n}f^{-1}(1-2x_{0})\right]\right\}$

(3-22)

という形になっている。ここで、f は何かしらの適当な関数、f⁻¹ はその逆関数を意味する。a = 4 では f (x) = cos x、a = 2 では f (x) = e ^x、a = −2 では f (x) = 2 cos (1/3(π − √3 x)) である。ただし、任意の a について一般的にロジスティック写像の厳密解を表すことができるような、数学的に標準的な関数の f は存在しない。

普遍性

同種の振る舞いを示す写像のクラス

正弦写像 (4-1) のグラフ

正弦写像 (4-1) の軌道図

ロジスティック写像で現れた上記の分岐のパターンは、ロジスティック写像に限定されない。ある条件を満たした写像で、この分岐パターンが共通して現れる。次の正弦関数を使った力学系はその一例である。

$x_{n+1}=b\sin \pi x_{n}$

(4-1)

ここで、定義域は 0 ≤ b ≤ 1 かつ 0 ≤ x ≤ 1 とする。この正弦写像 (4-1) は、ロジスティック写像 (1-2) と定性的に同一の振る舞いを起こす。つまり、この写像でも、ロジスティック写像と同じようにパラメータ b の増加にともなって周期倍化ルートを経てカオスになり、さらにはカオス領域には窓が同じように存在している。

ロジスティック写像も正弦写像も区間 [0, 1] を [0, 1] へ写す1次元写像で、単峰と呼ばれる次の性質を満たしている。

1. f (0) = f (1) = 0 を満たす。
2. 写像は可微分で、[0, 1] 中に f ′(c) = 0 を満たす臨界点 c が唯一存在する。

一般的に、1パラメータ・1変数のある1次元写像が単峰で、頂点近辺を2次の多項式で近似できるような曲線であれば、具体的な写像の形に依存せずに、パラメータ範囲 3 ≤ a ≤ 3.56994… で見たような無限の周期倍化カスケードの分岐が起き、 さらに式 (3-13) で定義される比率 δ はファイゲンバウム定数 4.669… に一致する。

また、ロジスティック写像で現れた安定周期軌道の出現パターンにも普遍性がある。パラメータを c として、x_n+1 = cf(x_n) で表される単峰な写像では、2つの不動点が不安定であるようなあるパラメータ区間で様々な周期の安定周期軌道が出現し続け、その出現パターン（ある周期の安定周期軌道の出現回数と出現順序）は共通であることが知られている。つまり、この種の写像であれば、写像の具体的な形によらずに安定周期軌道の系列は同じとなる。ロジスティック写像の場合は 3 < a < 4 がそのパラメータ区間であったが、正弦写像 (4-1) では 0.71… < b < 1 が共通する安定周期軌道の系列が起きるパラメータ区間である。この普遍性のある安定周期軌道の系列はU系列と呼ばれる。

加えて、ロジスティック写像は区間 [0, 1] 上でシュワルツ微分が常に負であるという性質を持つ。ある （C ³ 級の）写像 f のシュワルツ微分とは、

$Sf(x)={\frac {f'''(x)}{f'(x)}}-{\frac {3}{2}}\left({\frac {f''(x)}{f'(x)}}\right)^{2}$

(4-2)

で定義される関数である。実際にロジスティック写像のシュワルツ微分を計算すると

$S(ax(1-x))={\frac {-6}{(1-2x)^{2}}}<0$

(4-3)

となり、a および x の値に依らずにシュワルツ微分は負となる。[0, 1] を [0, 1] へ写す1次元写像が単峰で負のシュワルツ微分を持てば、存在する安定周期軌道は多くても1つであるといった性質が知られる。

位相共役な写像

記号 ∘ で写像の合成を表すとする。一般的に、位相空間 X, Y について、2つの写像 f : X → X と g : Y → Y が同相写像 h : X → Y によって

$h\circ f=g\circ h$

(4-4)

という関係を持つとき、f と g は位相共役であるという。位相共役という概念は、力学系の研究上で重要な役割を果たす。位相共役な f と g は本質的に同一な振る舞いを示し、f の振る舞いが周期的であれば g も周期的であり、f の振る舞いがカオス的であれば g もカオス的である。

特に同相写像 h が線形であれば、f と g は線形共役であるという。全ての2次関数は他の全ての2次関数と線形共役にある。したがって、

$x_{n+1}=x_{n}^{2}+b$

(4-5)

$x_{n+1}=1-cx_{n}^{2}$

(4-6)

$x_{n+1}=d-x_{n}^{2}$

(4-7)

などは、任意のパラメータ a のロジスティック写像と線形共役である。式 (4-6) や式 (4-7) の形のものもロジスティック写像と呼ばれたりもする。特に式 (4-7) の形だと計算量が減るため、長時間を要する数値計算に向いている。

テント写像 (4-8) の軌道の様子。a = 4 のロジスティック写像と位相共役な関係を持つ。

また、a = 4 のロジスティック写像 f_a=4 は、次のテント写像 T (x) やベルヌーイシフト写像 B (x) と位相共役な関係にある。

$T(x_{n})={\begin{cases}2x_{n}&\left(0\leq x_{n}\leq {\frac {1}{2}}\right)\\2(1-x_{n})&\left({\frac {1}{2}}\leq x_{n}\leq 1\right)\end{cases}}$

(4-8)

$B(x_{n})={\begin{cases}2x_{n}&\left(0\leq x_{n}<{\frac {1}{2}}\right)\\2x_{n}-1&\left({\frac {1}{2}}\leq x_{n}\leq 1\right)\end{cases}}$

(4-9)

ロジスティック写像 f_a=4 が厳密にカオス的であることの証明や、f_a=4 の厳密解 (3-19) の導出に、これらの位相共役の関係を利用できる。

あるいは、記号力学系の考え方を導入して、上記で導入したような 0 と 1 の列から成る記号列空間上に定義される次のようなシフト写像 σ を考えるとする。

$\sigma (s_{0}s_{1}s_{2}\cdots )=(s_{1}s_{2}\cdots )$

(4-10)

ここで、s_i は 0 または 1 である。式 (3-18) で導入した集合 Λ 上で、ロジスティック写像 f_a>4 はシフト写像と位相共役であるので、これを利用して Λ 上の f_a>4 がカオス的であることを導ける。

生物個体数モデルとしてのロジスティック写像

離散型個体群モデル

ロジスティック写像は、イギリスの数理生物学者ロバート・メイの研究を発端にして、生物の個体数の変化を考える式として世に広まった。このような生物個体数としてのロジスティック写像では変数 x_n は、ある環境中に生息する生き物の個体数（より専門的には個体群サイズ）を意味する。さらに、個体がその環境から出たり、外部の個体が環境に入ってきたりしない場合（あるいは移出入があっても実質的な影響がない場合）を想定しており、このような状況での個体数の増減を考える数理モデルが数理生物学上のロジスティック写像である。

生物の個体数の増殖を考える数理モデルには、差分方程式を使った離散的な時間のモデルと微分方程式を使った連続的な時間のモデルの2種類がある。例えば、卵を産むとすぐに死ぬような種類の昆虫では、その昆虫の個体数は、1世代目の個体数、2世代目個体数…というように各世代ごとに数えられる。このような例は、前者の離散時間モデルに適合する。一方で、各世代が連続的に重なり合っているような場合は、連続時間モデルと親和性がある。ロジスティック写像は、このような離散型あるいは世代分離型の個体群モデルに相当する。

ある環境中の単一種の生物の個体数を N で表すとする。もっとも単純な個体数の増殖の仕方として、個体数に対して常に一定の割合で増え続けるモデルが考えられる。そのような個体数増加モデルはマルサスモデルと呼ばれ、次のような形で表される。

$N_{n+1}=\alpha N_{n}$

(5-1)

ここで、N_n は n 世代目の個体数を意味しており、α は個体数の増殖率で正の定数である。しかし、モデル (5-1) では個体数が無尽蔵に増え続け、ほとんどの実現象に対して非現実的なモデルといえる。ある環境が養える個体数には限度があるので、個体数 N_n が増えていくと増殖率 α は低下していくのが自然に思われる。このように個体数密度の変化によって増殖率が変化することを密度効果と呼ぶ。密度効果をモデル (5-1) に反映した改良モデルとして、もっとも単純なものとして次のような差分方程式が考えられる。

$N_{n+1}=(a-bN_{n})N_{n}$

(5-2)

ここで、a はその環境中で可能な最大増殖率を意味し、b は密度効果の影響の強さを意味している。モデル (5-2) は、増殖率が個体数に単純に比例して下がっていくと想定している。式 (5-2) の N_n を

$x_{n}={\frac {b}{a}}N_{n}$

(5-3)

と変数変換すると、以下のロジスティック写像が導出される。

$x_{n+1}=a(1-x_{n})x_{n}$

(5-4)

生物の個体数として式 (5-2) あるいは式 (5-4) を扱う際には、N_n あるいは x_n が負になると個体数としての意味を為さなくなる。そうならないために、初期値 x₀ に対して 0 ≤ x₀ ≤ 1 という条件が、パラメータ a に対して 0 ≤ a ≤ 4 という条件が要求される。

他には、想定している環境が養える最大の個体数 K を仮定し、これを使って

$N_{n+1}=a\left(1-{\frac {N_{n}}{K}}\right)N_{n}$

(5-5)

という形で密度効果を取り込んだ差分方程式を考え、x_n = N_n/K と変数変換してロジスティック写像を導くこともある。この場合、変数 x_n は、最大個体数 K に対する個体数 N_n の比率を意味している。

ロジスティック方程式の離散化

ロジスティック写像は、連続時間型の個体群モデルのロジスティック方程式の離散化からも導出できる。ロジスティック写像の名も、ロバート・メイがロジスティック方程式の離散化からロジスティック写像を導入したことに由来する。ロジスティック方程式とは、次のような生物個体数の時間変化を表す常微分方程式である。

${\frac {dN}{dt}}\ =rN\left(1-{\frac {N}{K}}\right)$

(5-6)

ここで、N は生物個体数や個体数密度、t は連続的な時間、K と r がパラメータである。K は環境収容力、 r は内的自然増加率とも呼ばれ、通常は正の値を取る。この式の左辺 dN/dt は時刻 t における個体群サイズの変化速度を意味している。

ロジスティック方程式の解の例。個体数 N は時間 t が経過すると初期値によらず環境収容力 K に収束する。

ロジスティック方程式 (5-6) は、ロジスティック写像 (5-4) と一見似ているが、解の振る舞いはロジスティック写像とは大きく異なる。初期値 N₀ が正である限り、ロジスティック方程式の個体数 N は常に単調に K に収束するのみである。

このロジスティック方程式に、1階常微分方程式の数値解法の一つであるオイラー法による差分化近似を施すことによって、ロジスティック写像が導出できる。オイラー法の差分化近似とは、適当な時間間隔（時間刻み幅）Δt を導入し、増殖率 dN/dt を以下のように近似することである。

${\frac {dN}{dt}}\approx {\frac {N(t+\Delta t)-N(t)}{\Delta t}}$

(5-7)

この近似の結果、次のロジスティック写像が導かれる。

$x_{n+1}=ax_{n}(1-x_{n})$

(5-8)

ただし、この式の x_n と a は、元のパラメータ、変数、時間刻み幅と次のような関係を持つ。

$x_{n}={\frac {r\Delta t}{K(1+r\Delta t)}}N(n\Delta t)$

(5-9)

$a=1+r\Delta t$

(5-10)

Δt が十分小さければ、式 (5-8) は元の式 (5-6) の有効な近似として働き、Δt → 0では元の式の解と一致する。一方で、Δt が大きいと、元の式の解から外れていく。また、式 (5-10) の関係から、Δt を大きくすることはパラメータ a を大きくすることに相当する。よって、Δt を大きくするほど、元の方程式との誤差を単に大きくするだけでなく解にカオス的振る舞いを生み出すことになる。

位置付け

以上のように、生物の個体群動態論上では、ロジスティック写像は離散型増殖過程のモデルの一つである。ただし、生物の個体数のモデルとしてのロジスティック写像は、物理学の法則などとは異なり、直接的な実験結果や普遍的に成立する原理から導かれたものではない。導出過程の考え方にある程度の合理性はあるが、基本的には頭の中で考えられた「モデル」に留まる。ロジスティック写像を著名にしたメイも、論じているモデルが個体数の増減を正確に表現していると主張していたわけではない。生物個体群ダイナミクスの研究上も、歴史的に多用されてきたのは微分方程式による連続時間モデルであり、それら連続時間モデルの適用によって生物個体群ダイナミクスの理解を深めてきた。密度効果を考慮した離散時間個体群モデルとしても、個体数が負にならないリッカーモデルの方がより現実的と言える。

一般的に言えることとして、数理モデルは個体群ダイナミクスに関する重要な定性的情報を提供してくれることもあるが、実験的な裏付けがないのであれば、数理モデルから出てくる結果をあまり真剣に受け止めるべきではない。数理モデルの結論が生物学的研究結果から外れることがあっても、なおも数理モデルによる研究が有意義なのは、有用な対照となりうるからである。モデルの構成過程や設定、あるいはモデルが前提としていた生物学的な知見や仮説を見直すことにより、生物学的論点を提示できる可能性がある。生物個体数モデルとしてのロジスティック写像は単純過ぎて現実的ではないが、ロジスティック写像が示す結果は、環境からの不規則的な影響などに無関係に、個体群それ自体に内在するダイナミクスによって個体数の多様な変動が起こる可能性を示唆している。

応用

結合写像系

1変数のロジスティック写像は、系としての自由度あるいは次元は 1 である。一方で実際の自然界では、時間的に乱れるだけでなく、多数の空間自由度を持ち空間的にも乱れるような多自由度のカオスが多いと考えられる。あるいは、カオス的運動を行う振動子の同期現象も研究対象である。こういったものを調べるために、差分方程式（写像）を多数結合させる結合写像の手法がある。結合写像モデル研究の題材として、ロジスティック写像がしばしば採用される。その理由には、ロジスティック写像自体はすでにカオスの典型的モデルとしてよく調べられており、その蓄積があることが挙げられる。

結合写像モデルでの具体的な結合のさせ方には、様々な手法が存在する。全部で N 個の写像が結合し、i 番目の写像の時刻 n における状態が x_n(i) で表されるとする。大域結合写像と呼ばれる手法では、x_n+1(i) を次のように定式化する。

$x_{n+1}(i)=(1-\epsilon )f(x_{n}(i))+{\frac {\epsilon }{N}}\sum _{j=1}^{N}f(x_{n}(j))$

(6-1)

結合振動子の研究の流れでは、次のように変数の差分で振動子2つ x と y を結合させた最も簡単な次のモデルなどが挙げられる。

${\begin{cases}x_{n+1}=f(x_{n})+D(f(y_{n})-f(x_{n}))\\y_{n+1}=f(y_{n})+D(f(x_{n})-f(y_{n}))\end{cases}}$

(6-2)

これらの式中の f (x) が、結合写像モデルに組み込む具体的な写像であり、ロジスティック写像が用いられる場合はここに適用される。

a = 3.8 と D = 0.43 の結合写像モデル (6-2) の2つの変数の変化（上）とそれらの差（下）。2つの変数は、同期の後に不意に非同期状態になり、また同期状態に戻る。

式 (6-1) および (6-2) 中の ε や D は結合係数などと呼ばれる、写像同士の結合の強さを意味するパラメータである。他方で、ロジスティック写像を結合写像モデルに組み込む場合、ロジスティック写像のパラメータ a はモデルの非線形性の強さを意味する。a の値と ε または D の値を変化させることで、ロジスティック写像の結合写像系では様々な現象が現れる。例えばモデル (6-2) では、D をある値 D_c 以上に大きくすると、x と y は同期しながらカオス振動を行う。D_c 未満でも常にバラバラのカオス振動が起こるだけでない。D がある範囲のときは、a = 4 であるにもかかわらず x と y は2周期振動を起こす。a = 3.8 では、同期状態と非同期状態が交互に起こり続けるような振る舞いも見られる。

大自由度の大域結合写像 (6-1) にロジスティック写像を適用した研究では、カオス的遍歴と呼ばれる現象も見つかっている。これはいくつかのクラスターでまとまって振動する秩序的な状態から乱れた状態になり、また別のクラスター状態になり、再度乱れた状態になり…、という振る舞いを繰り返す現象で、相空間上でアトラクタの残骸と言われるような領域を軌道が経巡ることで起こると考えられている。

擬似乱数生成器

コンピューターシミュレーションや情報セキュリティ分野では、計算機で擬似乱数を作成することが重要な技術の一つで、擬似乱数を作る手法の一つとしてカオスの活用が考えられる。カオスからの擬似乱数生成器で十分な性能を持つものはまだ実現されていないが、これまでにいくつかの手法が提案されてきた。ロジスティック写像についても、これまでにカオスに基づく擬似乱数生成器の可能性が複数の研究者たちによって調べられてきている。

ロジスティック写像の擬似乱数生成には、パラメータ a = 4 がよく利用されている。歴史的にも、後述の通り、電子計算機の誕生から間もない1947年にスタニスワフ・ウラムとジョン・フォン・ノイマンも a = 4 のロジスティック写像を使った擬似乱数生成器の可能性を指摘している。しかし、ロジスティック写像 f_a=4 の点の分布は、式 (3-17) で示されるような分布になっており、出てくる数値が 0 と 1 の近くに偏る。そのため、偏りのない一様乱数を得るためには何らかの処理が必要となる。その方法としては、

1. 得られた数値をテント写像 (4-8) との関係を用いて一様分布に変換する方法
2. 得られた数値を上述のコイン投げの比喩のように閾値を使って 0 か 1 に変換し、これを繰り返して一様乱数のビット列を得る方法

などがある。また、ロジスティック写像で得られる数列の x_n とx_n+1 には強い相関があり、擬似乱数の数列としては問題となる。これを解消する方法の一つは、写像1回適用ごとの数列 x₀, x₁, x₂, … を作るのではなく、適当な τ > 1 回反復ごとに数列 x₀, x_τ, x_2τ, … を作る必要がある。例えば、1番の方法に対しては τ > 10 または τ > 13 で、2番の方法に対しては τ > 16 で良好な擬似乱数が得られるといわれる。

コンピュータを用いてデジタルにカオスを計算する一般的問題として、コンピュータでは有限計算精度で計算するため、カオス本来の真に非周期な数列を原理的に得ることができず代わりに有限の周期列が出力されるという問題点がある。原理的に非周期列が得られない場合であっても、擬似乱数生成のためにはできるだけ長い周期の数列が望ましい。しかし、単精度浮動小数点数計算でロジスティック写像 f_a=4 が実際に出力する数列の周期性を調べた結果によると、割り当てられたビット数から可能な最大周期に比べて実際に出力される数列の周期はとても小さくなることが報告されており、この観点からメルセンヌ・ツイスタのような既存の擬似乱数生成器に比べてロジスティック写像による擬似乱数生成は劣ると指摘されている。また、ロジスティック写像 f_a=4 では、計算途中で数値が不動点 0 に落ち入り、そのまま一定値になるおそれもある。一方で、ロジスティック写像では、開区間 (0, 1) の中で常に値を取るので、浮動小数点だけでなく固定小数点でも問題無く計算でき、固定小数点計算の利点を享受できる。固定小数点であれば、同じビット数で比較して浮動小数点よりも長い周期の数列になることや意図しない 0 への収束が無くせることが指摘されている。

複素数への拡張

ロジスティック写像の軌道図（上）とマンデルブロー集合（下）の対応関係

複素解析関数で定義された力学系も興味を持たれる対象である。その例が、次の2次関数で定義される力学系である。

$z_{n+1}=z_{n}^{2}+c$

(6-3)

ただし、ここでのパラメータ c と変数 z は複素数である。この写像は、ロジスティック写像 (1-2) と基本的には同じものと言える。上記でも述べたとおり、写像 (6-3) は、線形関数によってロジスティック写像 (1-2) と位相共役な関係にある。

パラメータ c を固定し、初期値 z₀ を変えながら写像 (6-3) の反復の行く末を計算したとき、n → ∞ でも z_n が無限大へ発散しないような z₀ の集まりを充填ジュリア集合という。さらに、充填ジュリア集合の境界をジュリア集合という。また、初期値を z₀ = 0 に固定し、パラメータ c を変えながら写像 (6-3) の反復を計算したとき、 z が無限大へ発散しないような c の集まりをマンデルブロー集合という。写像 (6-3) のジュリア集合やマンデルブロー集合から、「神秘的に見える」「怪奇を極めている」などと形容されるフラクタル図形が生成される。

特にマンデルブロー集合では、図形の各円板はある周期の漸近安定な周期軌道の領域に相当する。ロジスティック写像の軌道図とマンデルブロー集合の図形を並べると、ロジスティック写像軌道図の漸近安定な不動点、周期倍化分岐、周期3の窓などがマンデルブロー集合図形と実軸上で対応していることが分かる。

時間遅れを持つ場合

遅延ロジスティック写像の軌道の様子。左右の図で初期値 (x₀, y₀) は同じだが、a = 2 での分岐を境に軌道が引き付けられる先が閉曲線（左）と点（右）に分かれる。

ロジスティック写像を生物の各世代の個体数を表すモデルと解釈すると、次の世代の個体数が現在の世代の個体数だけでなく、その1つ前の世代の個体数も現在の世代に影響する場合も考えられる。そのような例が

$x_{n+1}=ax_{n}(1-x_{n-1})$

(6-4)

という差分方程式で、1つ前の世代の個体数 x_n−1 がマイナスの密度効果として式に取り込まれている。x_n+1 = y_n とおけば、式 (6-4) は次のような2変数差分方程式に置き換えられる。

${\begin{cases}x_{n+1}=y_{n}\\y_{n+1}=ay_{n}(1-x_{n})\end{cases}}$

(6-5)

この力学系は準周期アトラクタの分岐の研究などに用いられ、遅延ロジスティック写像やディレイドロジスティックマップ（英語: delayed logistic map）と呼ばれる。遅延ロジスティック写像では a = 2 でネイマルク・サッカー分岐が起き、漸近安定な不動点が不安定になり、その不安定な不動点の周りに漸近安定な不変曲線ができる。

研究史

カオス命名以前

写像の反復が力学系と関連する意味を持つ以前の時代、数学者のガストン・ジュリアとピエール・ファトゥが複素関数の反復について研究していた。ジュリアとファトゥの研究は解析関数を中心とした広範なものだったが、とくに式 (6-3) でも示した以下の複素2次関数の振る舞いが1920年代に彼らによって研究された。

$z_{n+1}=z_{n}^{2}+c$

(7-1)

ジュリアとファトゥもジュリア集合の中にカオス的振る舞いを理解していたが、当時はコンピュータ・グラフィックスなども無かったこともあって、彼らに続く人物が現れず研究は止まってしまった。その後1970年代後半まで複素力学系の研究は下火が続き、複素平面上の写像が示す豊かな力学系的振る舞いが着目されるのはベノワ・マンデルブロなどの登場を待つことになる。

スタニスワフ・ウラム

ジョン・フォン・ノイマン

1947年、数学者のスタニスワフ・ウラムとジョン・フォン・ノイマンは “On combination of stochastic and deterministic processes”（参考訳：確率論的過程と決定論的過程の結合に関して）と題した短いレポートで、

$f(x)=4x(1-x)$

(7-2)

という2次関数の反復合成によって疑似乱数を生成できることを指摘している。この式は、現在的な視点では a = 4 のロジスティック写像に相当する。この当時、「カオス」という言葉もまだ使われていないが、ウラムとフォン・ノイマンは非線形関数による複雑な数列の生成にすでに注目していたといえる。また、ウラムとフォン・ノイマンのレポートでは、写像 (7-2) とテント写像が位相共役の関係にあることや、この写像の数列の不変測度が式 (3-17) で与えられることも明らかにした。

その後、任意のパラメータ a を備えた形式の2次写像についても、詳細な調査がいくつかあった。1958年から1963年にかけて、フィンランドの数学者ペッカ・ミュルバーク は、λ をパラメータとする

$f(x)=x^{2}-\lambda$

(7-3)

という形式の2次写像の分岐現象を調べた。この一連の研究は力学系として本質的なもので、ミュルバークは、この写像の周期倍加分岐カスケードを調査して集積点 λ = 1.401155189… の存在も示している。他には、1964年のソビエトのオレクサンドル・シャルコフスキー、1969年のフランスのイーゴリ・グモウスキーとクリスチャン・ミラ 、1973年のニコラス・メトロポリスらの仕事などが、ロジスティック写像のような単純な1変数差分方程式の異常な振る舞いを明らかにしている。

ロバート・メイの研究

ロバート・メイ（2009年撮）

その後1970年初頭に、数理生物学者のロバート・メイが、生態学の問題に取り組む過程で式 (1-2) のモデルに出会う。メイはロジスティック方程式の離散時間化から式 (1-2) すなわちロジスティック写像を導入した。ロジスティック写像の振る舞いを数理的に解析し、メイは1973年や1974年にその成果を発表した。ロジスティック写像の数値実験が行われ、パラメータ a による振る舞いの変化が調べられた。1976年には、”Simple mathematical models with very complicated dynamics”（参考訳：極めて複雑な振る舞いを有する単純な数理モデル）と題した論文を Nature から発表した。

1976年の論文はレビュー論文で、ロジスティック写像を題材にしながら、単純な非線形関数でも周期倍化分岐カスケードやカオスのような非常に複雑な振る舞いが起こることについて強調し、注意を促す内容であった。特にこの論文は、メイの数理生物学者としての地位、研究結果の明快さ、そして何よりも単純な放物線の式が驚くべき複雑な振る舞いを生み出すという衝撃的な内容によって、大きな反響を巻き起こして科学界へと受け入れられた。このようなメイの研究を経て、ロジスティック写像は多くの研究者をカオス研究へ惹きつけ、カオス研究の流れを改めて再スタートさせたと評されるほど著名な数理モデルとなった。

メイの研究以後

メイは、ティェンイェン・リーとジェームズ・ヨークが論文 ”Period three implies chaos”（参考訳：3周期はカオスを意味する）で使った「カオス」という表現を積極的に用い、この論文にも注目を集めた。異論もあるが、このリーとヨークの論文は「カオス」という語を数学用語として最初に使ったと考えられており、同論文によって決定論的な無秩序的振る舞いを指す用語「カオス」が生まれたとされる。リーとヨークは、1973年に同論文を一旦完成させたが、The American Mathematical Monthly に投稿したところ研究色が強過ぎるので分かりやすく大幅に書き直すように告げられ、掲載を却下された。その後、論文は書き直されることなく放っておかれていた。しかし、翌1974年にリーとヨークが居たメリーランド大学にメイが特別招待講義にやってきて、ロジスティック写像の話をした。当時、メイは、ロジスティック写像のカオス領域で何が起きているのかまだ理解できていなかったが、リーとヨークもまた、ロジスティック写像の周期倍化カスケードについて知らなかった。メイの話に興奮したリーとヨークは、講義後にメイを捕まえて2人が得た結果の話をし、メイもその結果に驚いた。すぐにリーとヨークは却下された論文を書き直して、再提出された論文は1975年に出版された。

ミッチェル・ファイゲンバウム（2006年撮）

また1975年頃、数理物理学者のミッチェル・ファイゲンバウムは、ロジスティック写像の周期倍化カスケードに注目すると、分岐値が等比級数的に収束するスケーリングの法則に気づき、今ではファイゲンバウム定数と呼ばれる定数の存在を数値実験から発見した。メイもジョージ・オスターとともにそのスケーリング則に気づいていたが、深く追うことまではできなかった。ファイゲンバウムは、式 (4-1) で示した正弦写像でも同じ定数が現れることを発見し、このスケーリング則にはロジスティック写像だけに留まらない普遍性があることを知った。1980年には、この結果に対する厳密な証明がピエール・コレ、ジャン＝ピエール・エックマン、オスカー・ランフォードらによって与えられた。ファイゲンバウムとほぼ同時期あるいはその後、物理学者たちによって実現象に同じ周期倍化カスケードとファイゲンバウム定数が発見され、あくまでも数学的現象と見られていたカオスは物理学方面にも大きな衝撃を与えることとなる。

ただし、カオス流行以前の研究成果が軽視され、それらの研究成果の多くまでもがロジスティック写像などを用いた再発見者の功績扱いされる風潮への批判もある。メイ自身も先行研究があったことを尊重した上で、自身の功績は「2次写像の奇怪な数学的挙動を独立に最初に発見」したのではなく、自分は「科学におけるその広範な意味づけを最後に強調した研究者たち」の一人であると位置付けている。数学者のロバート・デバニーは、自著でロジスティック写像の解説に入る前に次のように語っている。

これにより、単に2次関数 f_λ(x) = λx(1 − x)（これもまたロジスティック写像と呼ばれる）を反復すれば、最初の個体数 x₀ の運命が予測できるようになるというわけだ。簡単な話のように聞こえるだろうが、あえて言い添えておくならば、この単純な2次関数の反復が完全に理解できるようになったのは、何百人もの数学者の努力の末、やっと1990年代の終わり頃になってからのことなのである。

参照文献

※文献内の複数個所に亘って参照したものを特に示す。

• 船越 満明、2008、『カオス』初版、朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7
• 早間 慧、2002、『カオス力学の基礎』改訂2版、現代数学社 ISBN 4-7687-0282-1
• 山口 昌哉、1986、『カオスとフラクタル ―非線形の不思議』、講談社〈ブルーバックス B-652〉 ISBN 4-06-132652-X
• デニー・グーリック、前田 恵一・原山 卓久（訳）、1995、『カオスとの遭遇 ―力学系への数学的アプローチ』初版、産業図書 ISBN 4-7828-1009-1
• K.T.アリグッド；T.D.サウアー；J.A.ヨーク、津田 一郎（監訳）、星野 高志・阿部 巨仁・黒田 拓・松本 和宏（訳）、2012a、『カオス　第1巻　力学系入門』、丸善出版 ISBN 978-4-621-06223-4
• K.T.アリグッド・T.D.サウアー・J.A.ヨーク、津田 一郎（監訳）、星野 高志・阿部 巨仁・黒田 拓・松本 和宏（訳）、2012c、『カオス　第3巻　力学系入門』、丸善出版 ISBN 978-4-621-06540-2
• 合原 一幸・黒崎 政男・高橋 純、1999、『哲学者クロサキと工学者アイハラの神はカオスに宿りたもう』初版、アスキー ISBN 4-7561-3133-6
• 小室 元政、2005、『基礎からの力学系 ―分岐解析からカオス的遍歴へ』新版、サイエンス社 ISBN 4-7819-1118-8
• 井上 政義・秦 浩起、1999、『カオス科学の基礎と展開 ―複雑系の理解に向けて』初版、共立出版 ISBN 4-320-03323-X
• Robert L. Devaney、國府 寛司・石井 豊 ・新居 俊作・木坂 正史（新訂版訳）、後藤 憲一（訳）、2003、『カオス力学系入門』新訂版、共立出版 ISBN 4-320-01705-6
• Steven H. Strogatz、田中 久陽・中尾 裕也・千葉 逸人（訳）、2015、『ストロガッツ　非線形ダイナミクスとカオス ―数学的基礎から物理・生物・化学・工学への応用まで』、丸善出版 ISBN 978-4-621-08580-6
• 合原 一幸、1993、『カオス ―まったく新しい創造の波』、講談社 ISBN 4-06-206287-9
• P.コレ、J-P.エックマン、森 真（訳）、1993、『カオスの出現と消滅 ―1次元単峰写像を中心として』第1版、遊星社 ISBN 4-7952-6873-8
• 香田 徹、1990、「カオス概論」、合原 一幸（編）『カオス ―カオス理論の基礎と応用』初版、サイエンス社〈Information & Computing 49〉 ISBN 4-7819-0592-7
• 下條 隆嗣、1992、『カオス力学入門 ―古典力学からカオス力学へ』初版、近代科学社〈シミュレーション物理学6〉 ISBN 4-7649-2005-0
• ロバート・M・メイ、ラルフ・エイブラハム；ヨシスケ・ウエダ（編）、稲垣 耕作・赤松 則男（訳）、2002、『カオスはこうして発見された』初版、共立出版 ISBN 4-320-03418-X
• 井上 政義、1996、『やさしくわかるカオスと複雑系の科学』初版、日本実業出版社 ISBN 4-53402492-4
• 今 隆助・竹内 康博、2018、『常微分方程式とロトカ・ヴォルテラ方程式』初版、共立出版 ISBN 978-4-320-11348-0
• Morris W. Hirsch; Stephen Smale; Robert L. Devaney、桐木 紳・三波 篤朗・谷川 清隆・辻井 正人（訳）、2007、『力学系入門　原著第2版 ―微分方程式からカオスまで』初版、共立出版 ISBN 978-4-320-01847-1
• 伊東 敬祐、1993、『カオスって何だろう ―予測できないカオスを予測する』、ダイヤモンド社 ISBN 4-478-83006-1
• 瀬野 裕美、2007、『数理生物学 ―個体群動態の数理モデリング入門』初版、共立出版 ISBN 978-4-320-05656-5
• ジェームス・D・マレー、三村 昌泰（総監修）、瀬野 裕美・河内 一樹・中口 悦史・三浦 岳（監修）、勝瀬 一登・吉田雄紀・青木 修一郎・宮嶋 望・半田 剛久・山下 博司（訳）、2014、『マレー数理生物学入門』初版、丸善出版 ISBN 978-4-621-08674-2
• 青木 統夫、1996、『力学系・カオス ―非線形現象の幾何学的構成』初版、共立出版 ISBN 4-320-03340-X
• 松葉 育雄、2011、『力学系カオス』第1版、森北出版 ISBN 978-4-627-15451-3
• 森 肇・蔵本 由紀、1994、『散逸構造とカオス』、岩波書店 ISBN 4-00-010445-4
• J. M. T. Thompson; H. B. Stewart、武者 利光（監訳）、橋口 住久（訳）、1988、『非線形力学とカオス ―技術者・科学者のための幾何学的手法』第1版、オーム社 ISBN 4-274-07431-5
• E. Atlee Jackson、田中 茂・丹羽 敏雄・水谷 正大・森 真（訳）、1994、『非線形力学の展望Ⅰ ―カオスとゆらぎ』初版、共立出版 ISBN 4-320-03325-6
• E. Atlee Jackson、田中 茂・丹羽 敏雄・水谷 正大・森 真（訳）、1995、『非線形力学の展望Ⅱ ―複雑さと構造』初版、共立出版 ISBN 4-320-03326-4
• ロバート・L・デバニー、上江洌 達也・重本 和泰・久保 博嗣・田崎 秀一（訳）、2007、『カオス力学系の基礎』新装版、ピアソン・エデュケーション ISBN 978-4-89471-028-3
• 丹羽 敏雄、1999、『数学は世界を解明できるか ―カオスと予定調和』再版、中央公論新社〈中公新書〉 ISBN 4-12-101475-8
• 山口 昌哉、1996、『カオス入門』初版、朝倉書店〈カオス全書1〉 ISBN 4-254-12671-9
• 井庭 崇・福原 義久、1998、『複雑系入門 ―知のフロンティアへの冒険』初版、NTT出版 ISBN 4-87188-560-7
• 瀬野 裕美、2016、『数理生物学講義 : 【基礎編】 数理モデル解析の初歩』初版、共立出版 ISBN 978-4-320-05781-4
• 池口 徹・山田 泰司・小室 元政、合原 一幸（編）、2000、『カオス時系列解析の基礎と応用』初版、産業図書 ISBN 978-4-7828-1010-1

• Kenneth Falconer、服部 久美子・村井 浄信（訳）、2006、『フラクタル幾何学』、共立出版〈新しい解析学の流れ〉 ISBN 4-320-01801-X
• フランコ・ヴィヴァルディ、ニ－ナ・ホ－ル（編）、宮崎 忠（訳）、1994、「数学的実験によるカオスの証明」、『カオスの素顔』、講談社〈ブルーバックス B-1029〉 ISBN 4-06-257029-7
• 金子 邦彦・津田 一郎、1996、『複雑系のカオス的シナリオ』初版、朝倉書店〈複雑系双書1〉 ISBN 4-254-10514-2
• ジェイムズ・グリック、上田 睆亮（監修）、大貫 昌子（訳）、1991、『カオス ―新しい科学をつくる』、新潮社〈新潮文庫 ク-18-1〉 ISBN 4-10-236101-4
• Robert M. May (1976). “Simple mathematical models with very complicated dynamics”. Nature 261: 459–467. doi:10.1038/261459a0. 

外部リンク

• Weisstein, Eric W. "Logistic Map". MathWorld (英語).
  • Weisstein, Eric W. "Logistic Map--r=-2". MathWorld (英語).
  • Weisstein, Eric W. "Logistic Map--r=2". MathWorld (英語).
  • Weisstein, Eric W. "Logistic Map--r=4". MathWorld (英語).