自然対数

実解析において実数の自然対数(しぜんたいすう、英: natural logarithm)は、超越数であるネイピア数 e (≈ 2.718281828459) を底とする対数を言う。x の自然対数を ln x や、より一般に loge x あるいは単に(底を省略して)log x などと書く[1]。 通常の函数の記法に則って引数を指示する丸括弧を明示的に付けて、ln(x) や log(x) などのように書いてもよい[注釈 1][2]。
定義により、x の自然対数とは 冪 et が x 自身に一致するような冪指数 t のことに他ならない。例えば、ln(7.5) = 2.0149… となることは、e2.0149… = 7.5 となることを理由とする。特に e の自然対数は ln(e) = 1, (⇔ e1 = e) であり、1 の自然対数は ln(1) = 0 (⇔ e0 = 1) である。[2]
自然対数は、任意の正数 a に対して 逆数函数 y = 1/x の 1 から a までの間のグラフの下にある面積(a < 1 のときは面積にマイナス記号をつけた値)として定義することもできる。この定義の単純さは自然対数を含む多くの公式によく馴染むことから、「自然」の語が冠されているのである。自然対数のこの定義は、負数や任意の非零複素数に対しても拡張することができる(ただし、それは多価函数を導く。複素対数函数の項を参照)。
実変数実数値の函数と見た自然対数函数 log は自然指数函数 exp の逆函数であり、それは二つの恒等式 exp(log(x)) = x (x > 0) と log(exp(x)) = x の成立を意味する。
他の任意の対数がそうであるように、自然対数は
なる意味で乗法を加法へ写す。これにより自然対数函数は正の実数の乗法群 (R+, ×) から実数の加法群 (R, +) への写像 log: R+ → R として 群の準同型になる。
e 以外にも、任意の正数 a ≠ 1 に対して、それを底とする対数を定義することができるが、そのような対数は自然対数の定数倍として得ることができる(例えば二進対数は自然対数の 1/ln 2 倍である)し、通常はそうして自然対数から定義される。対数は未知の量がほかの適当な量の冪と見なされる問題を解く際に有用で、例えば指数函数的減衰問題における減衰定数としての半減期を求めるときなどに利用できる。このように対数は、数学や自然科学の多くの分野において重要であり、また金融経済において複利を含む問題にも利用できる。
リンデマン–ヴァイアシュトラスの定理により、1 でない任意の(正の)代数的数に対してその自然対数は超越数となる。
| 自然対数 | |
| 表式 | |
| 逆函数 | |
| 導函数 | |
| 原始函数 | |
|
歴史[編集]
自然対数の概念が表立って現れるのは、1649年より以前にグレゴワール・ド・サン゠ヴァンサンとアルフォンス・アントニオ・ド・サラサによる[3]の成した業績においてであり、その中には双曲的扇形 の面積を決定することによる直交双曲線 xy = 1 の求積が含まれている。それら解法は、こんにち自然対数に結び付けられる性質を満足する「双曲対数」函数の必要から生じたものである。
自然対数への初期の言及はニコラス・メルカトルが1668年に著わした自身の著書 Logarithmotechnia(「対数の方法」)[4] にあるが、既に1619年には数学教師のジョン・スパイデルが事実上の自然対数表を編纂している[5]
記法の慣習[編集]
記法 "ln x" および "loge x" は何れも紛れなく x の自然対数を表しているが、底を明示しない記法 "log x" もまた自然対数を表すのに用いられることがある。このような記号の使い方は数学では広く用いられ、一部の自然科学の文脈やさまざまなプログラミング言語[注釈 2]でも用いられる。ただし、別の文脈では "log x" が常用対数(底 10 の対数)を表すのに用いられる。
符号位置[編集]
| 記号 | Unicode | JIS X 0213 | 文字参照 | 名称 |
|---|---|---|---|---|
| ㏑ | U+33D1 |
- |
㏑㏑ |
SQUARE LN |
「自然」の意味[編集]
直観的には、常用の記数法が底 10 の位取りであるため、10を底とする「常用対数」がよほど「自然」に感じられるかもしれない。だが、数学的に見れば10は何ら著しい特徴を持つ数ではなく、10 を用いるのは文化的な理由(典型的には両手の指の数が10本あること)からだ[6]。文化的な理由ではほかにも 5, 8, 12, 20, 60 などに基づく命数法がしばしば用いられる[7][8][9]。
自然対数 loge が「自然」であるというのは、数学において自然に生じ、よく見かけるということを根拠とするものである。例えば対数函数の微分の問題[10]
別な意味で底 e の対数が最も自然と思わせる理由として、単純な積分やテイラー級数でそれが極めて容易に定義できること(それは他の対数ではできない)が挙げられる。この自然さの更なる意味は、微分積分学の中では見えてこないが、例えば自然対数を含む単純な級数が様々存在することによって知ることができる。ピエトロ・メンゴリとニコラス・メルカトルがそれを「自然対数」(羅: logarithmus naturalis) と呼んだのは、ニュートンとライプニッツが微分積分学を繰り広げるよりも、何十年か先んじる[11]。
定義[編集]


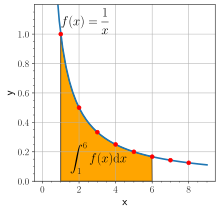
自然対数 ln は直交双曲線 1/x の面積として定義される。それは具体的には定積分として
と定めるということである。この函数は対数の基本性質 ln(ab) = ln(a) + ln(b) を満足するという意味において対数である。定数 e は ln(a) = 1 を満足する正数 a として定義される。
自然指数函数が先に(具体的には無限級数として)定義されている場合には、自然対数を自然指数函数の逆函数として定義することもできる。すなわち ln は exp(ln(x)) = x を満足する函数である。実数全体で定義された自然指数函数の値域は正数全体の集合に一致し、また自然指数函数は狭義単調増大(ゆえに一対一)であるから、ln はこの方法で任意の正数 x に対して矛盾なく定まる。
一般化[編集]
複素数の対数[編集]
0 でない複素数 z を極座標表示して
- z = r eiθ
と書けたとする。対数関数は指数関数の逆関数なので
- log z = ln r + iθ
ということになる(ln z と書くことはあまりない)が、この θ の選び方は一通りではなく 、2π の整数倍だけ異なる値を選ぶことができる。したがって、複素数の対数関数は多価正則関数である。
定義域を制限することによって、その定義域の上では正則な一価関数となるように θ の選び方を定めることができる。定義域は 0 を含まない単連結領域ならどれでもよいが、よく使われるのは複素平面から 0 と負の実数を除いた領域であり、変数の偏角を −π < θ < π の範囲にとる。このとき、r eiθ ↦ ln r + iθ によって正則な一価関数が得られる。この関数を対数関数の主値と呼び、
- Log z
と書く(Ln z と書くことはあまりない)。
複素対数関数は、実数での対数関数が満たす恒等式を満たすとは限らないので注意が必要である。例えば、Log ez = z や Log (zw) = Log z + Log w は一般には成り立たない。[注釈 3]
- 複素平面上での対数関数の主値
-
z = Re Log (x +iy)
-
z = | Im Log (x +iy) |
-
z = | Log (x +iy) |
-
これらを重ね合わせた図
バナッハ環における対数関数[編集]
|x| < 1 を満たす x に対して、テイラー展開
が可能である。この級数展開も、1668年にメルカトルによって見出されたものである。
すべての固有値の絶対値が 1 より小さい正方行列 X が与えられたとき、このテイラー展開の変数に X を代入することにより、行列 I + X の対数 ln (I + X ) が定義される。ここで、I は X と同じサイズの単位行列である。これをさらに一般化して、和や積の構造と両立するノルムを持った完備な空間であるバナッハ環において、ノルムが 1 より小さい元 x に対し、上の式によって 1 + x の対数が定義できる。このとき、指数関数による ln (1+x ) の像は可逆元 1+x になっている。
脚注[編集]
注釈[編集]
出典[編集]
- ^ Mortimer, Robert G. (2005). Mathematics for physical chemistry (3rd ed.). Academic Press. ISBN 0-12-508347-5—see pp. 9–11
- ^ a b “自然対数の底eの定義”. 金沢工業大学. 2024年3月5日閲覧。
- ^ Burn, R. P. (2001), “Alphonse Antonio de Sarasa and Logarithms”, Historia Mathematica 28: 1–17
- ^ J J O'Connor and E F Robertson (2001年9月). “The number e”. The MacTutor History of Mathematics archive. 2009年2月2日閲覧。
- ^ Cajori, Florian (1991). A History of Mathematics, 5th ed. AMS Bookstore. pp. 152. ISBN 0-8218-2102-4
- ^ A History of Mathematics (2 ed.). New York, USA: John Wiley & Sons. (1991-03-06). ISBN 978-0471543978. 0471543977
- ^ Harris, John (1987). “Australian Aboriginal and Islander mathematics” (PDF). Australian Aboriginal Studies 2: 29–37 2008年2月12日閲覧。.
- ^ Large, J.J. (1902). “The vigesimal system of enumeration”. Journal of the Polynesian Society 11 (4): 260–261 2011年3月30日閲覧。.
- ^ Cajori, Florian (1922). “Sexagesimal fractions among the Babylonians”. American Mathematical Monthly 29 (1): 8–10. doi:10.2307/2972914. JSTOR 2972914.
- ^ Larson, Ron (2007). Calculus: An Applied Approach (8th ed.). Cengage Learning. p. 331. ISBN 0-618-95825-8, p. 331, §4.5
- ^ Ballew, Pat. “Math Words, and Some Other Words, of Interest”. 2007年9月16日閲覧。
関連項目[編集]
外部リンク[編集]
- logarithm in nLab
- Weisstein, Eric W. "Natural Logarithim". mathworld.wolfram.com (英語).
- natural logarithim - PlanetMath.(英語)
- Hazewinkel, Michiel, ed. (2001), “Logarithm of a number”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel, ed. (2001), “Logarithmic function”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4







![{\displaystyle {\frac {d}{dx}}\log _{b}(x)={\frac {d}{dx}}\left({\frac {\ln(x)}{\ln(b)}}\right)={\frac {1}{\ln(b)}}\cdot {\frac {d}{dx}}[\ln(x)]={\frac {1}{x\ln(b)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2e14c60d7179e64f09a44751d6110980532b527)





