箱ひげ図

箱ひげ図(はこひげず、箱髭図、英: box plot、box-and-whisker plot)は、データの統計的ばらつきをわかりやすく表現するための統計図である。主に多くの水準からなる分布を視覚的に要約し、比較するために用いる。ジョン・テューキーが1970年代に提唱した。様々な分野で利用されるが、特に品質管理で盛んに用いられる。箱(box)と、その両側に出たひげ(whisker)で表現されることからこの名がある[1]。
定義
[編集]
箱ひげ図は五数要約(five-number summary)と呼ばれる(頑健な)要約統計量
- Q0/4: 最小値(minimum)
- Q1/4: 第1四分位点(lower quartile)
- Q2/4: 中央値(第2四分位点、median)
- Q3/4: 第3四分位点(upper quartile)
- Q4/4: 最大値(maximum)
を表すグラフである。第1四分位点から第3四分位点までの高さに箱を描き、中央値で仕切りを描く。ただし、ひげや外れ値、箱の幅・形などの扱いにはいくつか変種がある。簡明なのは最大値と最小値をひげの端で表したものである。外れ値も扱うときには閉区間
の外にあるものを(もしあれば)外れ値として個別に表示し、外れ値を除いたものの最大値・最小値にそれぞれひげの端をとる[2][3]。母集団は実際には様々なタイプの確率分布に従うわけだが、箱ひげ図はそのような仮定に関係なく、データの分布を表現することができる。箱の各部分の間隔から分散や歪度の程度を知ることもできる。
例
[編集]以下に箱ひげ図の具体例を挙げる:
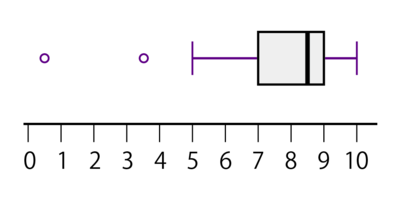
このデータセット(値は図から読み取れる概略値とする)から、次のことが分かる。
- 最小値 = 0.5
- 第1四分位点 = 7
- 中央値(第2四分位点) 8.5
- 第3四分位点 = 9
- 最大値 = 10
- 四分位範囲(IQR) = 2
- 3.5という値は"軽度の"外れ値、つまりQ1/4よりも 1.5×IQR から 3×IQR だけ下にある
- 0.5という値は"極端な"外れ値、つまりQ1/4よりも 3×IQR 以上下にある
- 外れ値以外の最小値は5
- データは左に歪んでいる(負の歪度)
"軽度"および"極端"外れ値の境は、箱の長さの2倍の点である。なお、この図からデータの平均値は読み取れない。
変種
[編集]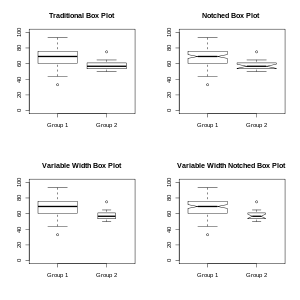
いろいろな統計パッケージで使われている箱ひげ図の中には、違う方式(例えば5%点と95%点をひげの端にする)を採用したものもある。このような方式は、中央値を中心とする分布を強調するテューキーの方式と異なり、またデータサイズが10を越えただけで(分布の形によらず)外れ値を出してしまう傾向がある。
脚注
[編集]- ^ 西岡康夫,数学チュートリアル やさしく語る 確率統計,1.6 箱ひげ図 p.13, オーム社, 2013, ISBN 9784274214073
- ^ Dekking et al. 2005, 16.4 The box-and-whisker plot.
- ^ R言語の
boxplotもデフォルトではこのようにプロットする。
参考文献
[編集]- Dekking, F. M.; Kraaikamp, C.; Lopuhaä, H. P.; Meester, L. E. (2005). A modern introduction to probability and statistics. Springer Texts in Statistics. Springer-Verlag. ISBN 978-1-85233-896-1. MR2208349
- 西岡康夫『数学チュートリアル やさしく語る 確率統計』オーム社、2013年。ISBN 9784274214073。
関連項目
[編集]外部リンク
[編集]- 総務省統計局. “箱ひげ図”. なるほど統計学高等部. 2016年3月29日閲覧。—Excelで箱ひげ図を作る方法
- “What is Box plot”. 2023年7月8日閲覧。—R言語で箱ひげ図を作る方法

![{\displaystyle [Q_{1/4}-1.5\,\mathrm {IQR} ,\,Q_{3/4}+1.5\,\mathrm {IQR} ]\qquad (\mathrm {IQR} =Q_{3/4}-Q_{1/4})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbb9eb9a34dd4ddb621b92546457334f53f7061)