熱力学ポテンシャル (ねつりきがくポテンシャル、英語 : thermodynamic potential )とは、熱力学 において、系の平衡状態 における熱力学的性質の情報を全て持つ示量性 状態量である。完全な熱力学関数 とも呼ばれる[1]
ウィラード・ギブズ は基本的な方程式 (fundamental equations)と呼んでいた[2]
「熱力学的性質の情報を全て持つ」とは全ての状態量がこの関数から(偏微分 等の組み合わせにより)与えられるという意味である。言い換えれば、完全な熱力学関数が与えられればそこから状態方程式 や熱容量などの系の性質が決まる[3] 凸性 など)を与えるが、具体的な関数形は実験的に決められるか、統計力学 から導出するなど、熱力学以外から与えられる[4]
熱力学ポテンシャルの一つである内部エネルギー U は、エントロピー S 、体積 V 、各成分の物質量 N = {N i [注釈 1] X を変数に持つ関数 U (S , N , V , X )エネルギー表示 と呼ばれることがある[5]
(
∂
U
∂
S
)
V
,
N
,
X
=
T
(
S
,
V
,
N
,
X
)
,
(
∂
U
∂
V
)
S
,
N
,
X
=
−
p
(
S
,
V
,
N
,
X
)
,
(
∂
U
∂
N
i
)
S
,
V
,
X
=
μ
i
(
S
,
V
,
N
,
X
)
,
(
∂
U
∂
X
)
S
,
V
,
N
=
x
(
S
,
V
,
N
,
X
)
{\displaystyle {\begin{aligned}\left({\frac {\partial U}{\partial S}}\right)_{V,N,X}&=T(S,V,N,X),\\\left({\frac {\partial U}{\partial V}}\right)_{S,N,X}&=-p(S,V,N,X),\\\left({\frac {\partial U}{\partial N_{i}}}\right)_{S,V,X}&=\mu _{i}(S,V,N,X),\\\left({\frac {\partial U}{\partial X}}\right)_{S,V,N}&=x(S,V,N,X)\end{aligned}}}
となり、熱力学温度 T 、圧力 p 、各成分の化学ポテンシャル μ = {μ i X に対応する示強性状態量[注釈 2] x が得られる。これらはエネルギー表示の示強性状態量 [5] 熱容量 や圧縮率 なども計算される。内部エネルギーの全微分 は
d
U
=
T
d
S
−
p
d
V
+
∑
i
μ
i
d
N
i
+
x
d
X
{\displaystyle dU=T\,dS-p\,dV+\sum _{i}\mu _{i}\,dN_{i}+x\,dX}
となる。
エネルギー表示の U
d
S
=
1
T
d
U
+
p
T
d
V
−
∑
i
μ
i
T
d
N
i
−
x
T
d
X
{\displaystyle dS={\frac {1}{T}}\,dU+{\frac {p}{T}}\,dV-\sum _{i}{\frac {\mu _{i}}{T}}\,dN_{i}-{\frac {x}{T}}\,dX}
となり、エントロピー S は内部エネルギー U 、体積 V 、物質量 N 、及びその他の示量性状態量 X を変数にもつ関数 S (U , V , N , X )エントロピー表示 と呼ぶ場合がある[5] エントロピー表示の示強変数 [5]
(
∂
S
∂
U
)
V
,
N
,
X
=
1
T
(
U
,
V
,
N
,
X
)
{\displaystyle \left({\frac {\partial S}{\partial U}}\right)_{V,N,X}={\frac {1}{T(U,V,N,X)}}}
などが得られる。しかし統計力学との関係からこの表示は重要である。ボルツマンの原理 により分配関数と直接的に関係づけられるのはエントロピー表示の熱力学ポテンシャルである。
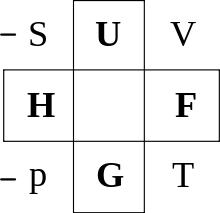
ルジャンドル変換 [ 編集 ] ボルンの熱力学的正方形[6] en:Thermodynamic square )は、ルジャンドル変換で繋がっている完全な熱力学関数とその変数を覚えやすくまとめたものである。 完全な熱力学関数には自然な独立変数 [4] U は、エントロピー S に替えて温度 T を変数に持つときには完全な熱力学関数とはならない。系の平衡状態を指定する状態変数の組が (T , V , N , X ) である場合は、ルジャンドル変換
d
F
=
d
(
U
−
T
S
)
=
−
S
d
T
−
p
d
V
+
∑
i
μ
i
d
N
i
+
x
d
X
{\displaystyle dF=d(U-TS)=-S\,dT-p\,dV+\sum _{i}\mu _{i}\,dN_{i}+x\,dX}
によってヘルムホルツエネルギー F (T , V , N , X )
エントロピーに対してもルジャンドル変換を考えることができて
d
Ψ
=
d
(
S
−
β
U
)
=
−
U
d
β
−
p
T
d
V
+
∑
i
μ
i
T
d
N
i
+
x
T
d
X
{\displaystyle d\Psi =d(S-\beta U)=-U\,d\beta -{\frac {p}{T}}\,dV+\sum _{i}{\frac {\mu _{i}}{T}}\,dN_{i}+{\frac {x}{T}}\,dX}
などの完全な熱力学関数を導入することができる[注釈 3] Ψ = −F /T の関係にある[7]
熱力学ポテンシャルとその変数の例[7]
表示
熱力学ポテンシャル
記号と定義
自然な変数
全微分形
エネルギー表示
内部エネルギー U (S , V , N )
dU = TdS − pdV + μdN
エンタルピー H = U + pV (S , p , N )
dH = TdS + Vdp + μdN
ヘルムホルツエネルギー F = U − TS (T , V , N )
dF = − SdT − pdV + μdN
ギブズエネルギー G = F + pV (T , p , N )
dG = − SdT + Vdp + μdN
グランドポテンシャル J = F − μN (T , V , μ )
dJ = − SdT - pdV − Ndμ
エントロピー表示
エントロピー S (U , V , N )
dS = (1/T )dU + (p /T )dV − (μ /T )dN
マシュー関数 (英語版 ) Ψ = S − U /T = −F /T (β , V , N ) [注釈 3] d Ψ = −Udβ + (p /T )dV − (μ /T )dN
Planck関数
Φ = Ψ − (p /T )V = −G /T (β , p /T , N ) [注釈 3] d Φ = −Hdβ − (V /T )dp − (μ /T )dN
Kramers関数
q = Ψ + αN = −J /T (β , V , α ) [注釈 3] dq = − Udβ + (p /T )dV + Ndα
ギブズ-デュエムの関係 [ 編集 ] 系のスケール変換を考えると、内部エネルギー U 、エントロピー S 、体積 V 、物質量 N の示量性から、任意の λ > 0
U
(
λ
S
,
λ
V
,
λ
N
)
=
λ
U
(
S
,
V
,
N
)
{\displaystyle U(\lambda S,\lambda V,\lambda N)=\lambda U(S,V,N)}
という1次同次性 が成り立つ。このことから
U
=
∂
U
∂
S
S
+
∂
U
∂
V
V
+
∑
i
∂
U
∂
N
i
N
i
=
T
S
−
p
V
+
∑
i
μ
i
N
i
{\displaystyle U={\frac {\partial U}{\partial S}}S+{\frac {\partial U}{\partial V}}V+\sum _{i}{\frac {\partial U}{\partial N_{i}}}N_{i}=TS-pV+\sum _{i}\mu _{i}N_{i}}
の関係が導かれる。他にも
H
=
U
+
p
V
=
T
S
+
∑
i
μ
i
N
i
,
F
=
U
−
T
S
=
−
p
V
+
∑
i
μ
i
N
i
,
G
=
F
+
p
V
=
∑
i
μ
i
N
i
,
J
=
F
−
∑
i
μ
i
N
i
=
−
p
V
{\displaystyle {\begin{aligned}H&=U+pV=TS+\sum _{i}\mu _{i}N_{i},\\F&=U-TS=-pV+\sum _{i}\mu _{i}N_{i},\\G&=F+pV=\sum _{i}\mu _{i}N_{i},\\J&=F-\sum _{i}\mu _{i}N_{i}=-pV\end{aligned}}}
などの関係式が得られる。
また、この式を微分すると
S
d
T
−
V
d
p
+
∑
i
N
i
d
μ
i
=
0
{\displaystyle S\,dT-V\,dp+\sum _{i}N_{i}\,d\mu _{i}=0}
の関係式が得られる。この関係式をギブズ-デュエムの関係 と言い、示強性状態量の組 (T , p , μ ) を系の平衡状態を指定する状態変数として選ぶことは出来ないことを表している。
平衡状態の安定性 [ 編集 ] 系が温度 T ex 熱力学第二法則 から、系に変化が起きるとき
δ
′
Q
≤
T
ex
δ
S
{\displaystyle \delta 'Q\leq T_{\text{ex}}\delta S}
である。一方、エネルギー保存則 から
δ
′
Q
=
δ
U
+
δ
′
W
=
δ
U
+
p
ex
δ
V
−
μ
ex
δ
N
{\displaystyle \delta 'Q=\delta U+\delta 'W=\delta U+p_{\text{ex}}\delta V-\mu _{\text{ex}}\delta N}
である。p ex μ ex
δ
U
−
T
e
x
δ
S
+
p
e
x
δ
V
−
μ
e
x
δ
N
≤
0
{\displaystyle \delta U-T_{\mathrm {ex} }\delta S+p_{\mathrm {ex} }\delta V-\mu _{\mathrm {ex} }\delta N\leq 0}
となる。系が平衡状態 にあるとき、変化が起こらない ので、
δ
U
−
T
e
x
δ
S
+
p
e
x
δ
V
−
μ
e
x
δ
N
>
0
{\displaystyle \delta U-T_{\mathrm {ex} }\delta S+p_{\mathrm {ex} }\delta V-\mu _{\mathrm {ex} }\delta N>0}
である。
これが成り立つ条件は、1次変分について
(
∂
U
∂
S
−
T
e
x
)
δ
S
+
(
∂
U
∂
V
+
p
e
x
)
δ
V
+
(
∂
U
∂
N
−
μ
e
x
)
δ
N
=
0
{\displaystyle \left({\frac {\partial U}{\partial S}}-T_{\mathrm {ex} }\right)\delta S+\left({\frac {\partial U}{\partial V}}+p_{\mathrm {ex} }\right)\delta V+\left({\frac {\partial U}{\partial N}}-\mu _{\mathrm {ex} }\right)\delta N=0}
および、2次変分について
1
2
(
∂
2
U
∂
S
2
δ
S
2
+
∂
2
U
∂
V
2
δ
V
2
+
∂
2
U
∂
N
2
δ
N
2
)
+
∂
2
U
∂
S
∂
V
δ
S
δ
V
+
∂
2
U
∂
S
∂
N
δ
S
δ
N
+
∂
2
U
∂
V
∂
N
δ
V
δ
N
>
0
{\displaystyle {\frac {1}{2}}\left({\frac {\partial ^{2}U}{\partial S^{2}}}\delta S^{2}+{\frac {\partial ^{2}U}{\partial V^{2}}}\delta V^{2}+{\frac {\partial ^{2}U}{\partial N^{2}}}\delta N^{2}\right)+{\frac {\partial ^{2}U}{\partial S\partial V}}\delta S\delta V+{\frac {\partial ^{2}U}{\partial S\partial N}}\delta S\delta N+{\frac {\partial ^{2}U}{\partial V\partial N}}\delta V\delta N>0}
である。
1次変分の条件から
系が熱を交換するとき(δS ≠ 0
∂
U
∂
S
≡
T
=
T
ex
{\displaystyle {\frac {\partial U}{\partial S}}\equiv T=T_{\text{ex}}}
系の体積が変化するとき(δV ≠ 0
∂
U
∂
V
≡
−
p
=
−
p
ex
{\displaystyle {\frac {\partial U}{\partial V}}\equiv -p=-p_{\text{ex}}}
系が物質を交換するとき(δN ≠ 0
∂
U
∂
N
≡
μ
=
μ
ex
{\displaystyle {\frac {\partial U}{\partial N}}\equiv \mu =\mu _{\text{ex}}}
などの平衡条件が得られる。
2次変分の条件からは
∂
2
U
∂
S
2
=
(
∂
T
∂
S
)
V
=
T
C
V
≥
0
{\displaystyle {\frac {\partial ^{2}U}{\partial S^{2}}}=\left({\frac {\partial T}{\partial S}}\right)_{V}={\frac {T}{C_{V}}}\geq 0}
∂
2
U
∂
V
2
=
−
(
∂
p
∂
V
)
S
=
1
V
κ
S
≥
0
{\displaystyle {\frac {\partial ^{2}U}{\partial V^{2}}}=-\left({\frac {\partial p}{\partial V}}\right)_{S}={\frac {1}{V\kappa _{S}}}\geq 0}
∂
2
U
∂
S
2
∂
2
U
∂
V
2
−
(
∂
2
U
∂
S
∂
V
)
2
=
T
C
p
1
V
κ
S
=
T
C
V
1
V
κ
T
≥
0
{\displaystyle {\frac {\partial ^{2}U}{\partial S^{2}}}{\frac {\partial ^{2}U}{\partial V^{2}}}-\left({\frac {\partial ^{2}U}{\partial S\partial V}}\right)^{2}={\frac {T}{C_{p}}}{\frac {1}{V\kappa _{S}}}={\frac {T}{C_{V}}}{\frac {1}{V\kappa _{T}}}\geq 0}
などが得られる[8] CV は定積熱容量 、Cp は定圧熱容量 、κS は断熱圧縮率 、κT は等温圧縮率 である。
平衡状態の安定性から熱力学ポテンシャルは一般に凸関数 となる。
統計力学との関係 [ 編集 ] 完全な熱力学関数は分配関数 と関係付けられる。巨視的な熱力学と微視的な統計力学 を結びつける関係である。
S
(
E
,
N
,
V
)
=
k
ln
W
(
E
,
N
,
V
)
{\displaystyle S(E,N,V)=k\ln W(E,N,V)}
F
(
β
,
N
,
V
)
=
−
1
β
ln
Z
(
β
,
N
,
V
)
{\displaystyle F(\beta ,N,V)=-{\frac {1}{\beta }}\ln Z(\beta ,N,V)}
J
(
β
,
μ
,
V
)
=
−
1
β
ln
Ξ
(
β
,
μ
,
V
)
{\displaystyle J(\beta ,\mu ,V)=-{\frac {1}{\beta }}\ln \Xi (\beta ,\mu ,V)}
ここで、β =1/kT 逆温度 である。k はボルツマン定数 である。
具体例 [ 編集 ] この節の
加筆 が望まれています。
(2020年12月 )
^ 例えば分極 P や磁化 M など。
^ 例えば分極 P に対応する外部電場 E や磁化 M に対応する外部磁場 H など。
^ a b c d β =1/T α =μ /T
^ 田崎『熱力学』 p.120^ 田崎『熱力学』 p.17^ 佐々真一 著、兵頭俊夫 編『熱力学入門』共立出版、2000年、76頁。ISBN 4-320-03347-7 。 ^ a b 久保『熱学・統計力学』 p.88
^ a b c d 清水『熱力学の基礎I』pp.94-98
^ 清水『熱力学の基礎II』p.2
^ a b 久保『熱学・統計力学』 p.90
^ 久保『熱学・統計力学』 p.97
参考文献 [ 編集 ]