カタランの立体
カタランの立体 (Catalan solid) は、半正多面体(アルキメデスの立体)の双対である。アルキメデス双対 (Archimedean dual) とも言う。半正多面体が13種類あるため、カタランの立体も13種類ある。
カタランとは、ベルギーの数学者ウジェーヌ・カタラン (Eugène Charles Catalan) のことで、1865年にこの図形について最初に記述した。
性質[編集]
半正多面体の双対であることから、多くの性質は半正多面体の性質と対応している。
半正多面体は頂点形状が合同であるため、カタランの立体は面が合同である。ただし、半正多面体は2種類の面を持つため、カタランの立体の面は正多角形ではなく、したがって、一様多面体ではない。
半正多面体の辺の長さが等しいことより、カタランの立体は全ての二面角が等しい。
半正多面体が外接球面を持つ一方、カタランの立体は内接球面を持つ。
一覧[編集]
| 名前 | 投影図 | 動画 | 双対 | 面 数 |
辺 数 |
頂 点 数 |
面の形状 | 対称性 |
|---|---|---|---|---|---|---|---|---|
| 三方四面体 | 
|

|
切頂四面体 | 12 | 18 | 8 | 二等辺三角形 V3.6.6 |
Td |
| 菱形十二面体 | 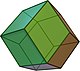
|

|
立方八面体 | 12 | 24 | 14 | 菱形 V3.4.3.4 |
Oh |
| 三方八面体 | 
|

|
切頂六面体 | 24 | 36 | 14 | 二等辺三角形 V3.8.8 |
Oh |
| 四方六面体 | 
|

|
切頂八面体 | 24 | 36 | 14 | 二等辺三角形 V4.6.6 |
Oh |
| 凧形二十四面体 | 
|

|
斜方立方八面体 | 24 | 48 | 26 | 凧形 V3.4.4.4 |
Oh |
| 六方八面体 | 
|

|
斜方切頂立方八面体 | 48 | 72 | 26 | 三角形 V4.6.8 |
Oh |
| 五角二十四面体 |  
|
 
|
変形立方体 | 24 | 60 | 38 | 2辺と3辺が等しい五角形 V3.3.3.3.4 |
O |
| 菱形三十面体 | 
|

|
二十・十二面体 | 30 | 60 | 32 | 菱形 V3.5.3.5 |
Ih |
| 三方二十面体 | 
|

|
切頂十二面体 | 60 | 90 | 32 | 二等辺三角形 V3.10.10 |
Ih |
| 五方十二面体 | 
|

|
切頂二十面体 | 60 | 90 | 32 | 二等辺三角形 V5.6.6 |
Ih |
| 凧形六十面体 | 
|

|
斜方二十・十二面体 | 60 | 120 | 62 | 凧形 V3.4.5.4 |
Ih |
| 六方二十面体 | 
|

|
斜方切頂二十・十二面体 | 120 | 180 | 62 | 三角形 V4.6.10 |
Ih |
| 五角六十面体 |  
|
 
|
変形十二面体 | 60 | 150 | 92 | 2辺と3辺が等しい五角形 V3.3.3.3.5 |
I |

