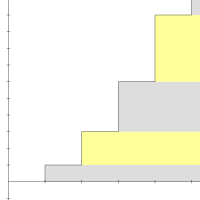
1+2+3+4+…
自然数すべての総和 1 + 2 + 3 + 4 + … は、その n-次の部分和
が三角数によって与えられる無限級数。これは n を無限大に飛ばすとき際限なく増加するため、この級数は(正の無限大に)発散し、通常の意味での「和」を持たない。
一見するとこの級数が意味のある値を持つことは全くないように思われるが、これに数学的に意味のある値を結びつける方法があり、そうして得られた値は複素解析や、物理学における場の量子論、特に弦理論などの分野において応用がある。様々な総和法を用いることで、上記のごとき発散級数にさえ有限な数値を割り当てることができ、特にゼータ関数正規化やラマヌジャン総和法では件の級数に −1/12 を値として割り当てる。この事実をよく知られた公式
として式に表す[1][2]。モンスター群のムーンシャイン現象に関するモノグラフでテリー・ガノンはこの等式を「自然科学において最も注目すべき公式の一つ」と評した[3]。
部分和について
[編集]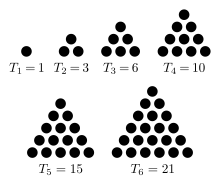
級数 1 + 2 + 3 + 4 + 5 + … の部分和は順に 1, 3, 6, 10, 15, … と続き、第 n 部分和は簡単な公式
によって与えられる。この等式はピタゴラス学派によって紀元前6世紀ごろには早くも知られていた[4]。この形で与えられる数は、各項を点を三角形状に並べることで数えられることから、三角数と呼ばれる数である。
三角数からなる無限数列は +∞ に発散するから、定義により無限級数 1 + 2 + 3 + 4 + … もまた +∞ に発散する。これが発散することは「項が 0 に収束しないならば級数は発散する」という項判定法の単純な帰結でもある。
ゼータ関数の部分和
[編集]リーマンゼータ関数を部分和にした
を複素平面上にプロットした時、の虚部に対してが十分大きくなると対数螺旋のような軌跡を描く。その軌跡の中心は元となったゼータ関数の値に近似していることが観測されており[5]、の実部をとして虚部を十分小さくした時にこの方法でを観測すると −1/12に近似する(函数等式)。[6]
総和可能性について
[編集]様々知られた古典的な発散級数の中でも 1 + 2 + 3 + 4 + … は有限値へ持ち込むことが比較的難しい。発散級数に有限な数値を割り当てる総和法は多数存在するが、それらの中には総和法としての強さが比較可能なものがある。例えば、チェザロ総和法は緩やかに発散するグランディ級数 1 − 1 + 1 − 1 + … を 1/2 に総和することはよく知られているが、アーベル総和法はグランディ級数を 1/2 に総和するのみならず、より扱いの難しい級数 1 − 2 + 3 − 4 + … までも 1/4 に総和することができる。
これらの級数と異なり、1 + 2 + 3 + 4 + … はチェザロ総和可能でもアーベル総和可能でもない。これらの総和法が適用できるのは収束級数と振動級数に対してのみであり、+∞ に発散する級数については有限な値を生み出すことはできないのである[7]。そこでより発展的な総和法が必要になるのであるが、それは例えばゼータ関数正規化やラマヌジャン総和法である。だいたいそういった方法による経験論を用いて、この級数の値が −1/12 であると論ずることができる。
ヒューリスティックな説明
[編集]
ラマヌジャンは彼のノートブックの8章において "1 + 2 + 3 + 4 + … = −1/12" の導出を二種類の方法で与えている[8][9][10]。厳密さをさておいて簡単に述べれば以下のようなことになる。
考察の第一の鍵は、正項級数 1 + 2 + 3 + 4 + … が交項級数 1 − 2 + 3 − 4 + … にきわめてよく似ていることである。後者の級数もまた発散するのであるが、扱いは極めて容易で、これに値を割り当てる古典的な総和法がいくつか存在し、それは18世紀にはすでに発見されていた[11]。
さて級数 1 + 2 + 3 + 4 + … を級数 1 − 2 + 3 − 4 + … に変形するのに、第二項から 4 を引き、第四項から 8 を引き、第六項から 12 を引き……、という具合にやって行けば、引かれる総量は 4 + 8 + 12 + 16 + … でこれはもとの級数の 4 倍である。これを少し代数学的に書いてみよう。この級数の「和」となるべきものがあるとしてそれを c = 1 + 2 + 3 + 4 + … と呼ぶことにすると、これを 4 倍してもとの式から引けば
を得る。
考察の第二の鍵は、交項級数 1 − 2 + 3 − 4 + … が 1/(1 + x)2 の形式冪級数展開に x = 1 と代入したものになっていることである。ラマヌジャンのノートに従えば
の両辺を −3 で割って、c = −1/12 を得る。
一般論で言えば、無限級数を(特に発散級数を)有限和と同様のものであるかのように扱うことは危険である。例えば発散級数に対してその任意の位置に無数の 0 を挿入することでさえ、自己矛盾した結果を導き得る(まして他と整合する結果であることをあらかじめ望むべくもない)。特に、4c = 0 + 4 + 0 + 8 + … とした手順は、単に加法単位元の基本性質のみで正当化することができるものではないのである。さらに極端な例として、級数の先頭にたった一つ 0 を付け加えるだけで矛盾した結果を導くことができることさえある[12]。
この状況を改善して 0 の挿入可能な場所を制限する一つの方法は、適当な関数に従って配置することによって各項のつながり方を保つことである[注釈 1]。級数 1 + 2 + 3 + 4 + … における各項 n は単なる数であるが、ここで項 n を複素変数 s に関する関数 n−s へ昇華するならば、項が足し合わされるというようなことだけについては保証することができるようになる。そうして得られた級数はより厳密な取扱いができるようになるし、そのあとで変数 s を −1 に特殊化することもできる。こういった手法を形にしたものがゼータ関数正規化である(後述)。
ゼータ関数正規化
[編集]
ゼータ関数正規化 (zeta function regularization) において、級数 は級数 に置き換えられる。後者の級数はディリクレ級数の一例である。複素変数 s の実部が 1 より大きいときこのディリクレ級数は収束し、その和はリーマンゼータ関数 ζ(s) に等しい。一方、実部が 1 以下のときこのディリクレ級数は発散し、特に級数 1 + 2 + 3 + 4 + … は s = −1 と置いたものだから、1 + 2 + 3 + 4 + … は発散する。リーマンゼータ関数を導入するメリットは、そうすれば s に関する解析接続によって級数の収束領域の外側まで矛盾なく定義することができることにある。そうして、級数 1 + 2 + 3 + 4 + … のゼータ関数正規化された「和」を ζ(−1) = −1/12 と定義するのである[注釈 2]。
ところで、ζ(−1) = −1/12 を証明する方法はいくつか知られている。一つの方法はオイラーの論法に沿ったもので、リーマンゼータ関数とディリクレイータ関数 η(s) との間の関係を用いる[14]。このイータ関数は交代ディリクレ級数によって定義されるもので、故にこの方法は古き経験論的方法をなぞるものである。両ディリクレ級数が収束する領域において、等式
が成り立ち、この等式 は、上記の級数が発散する領域の s に対しても、解析接続によって延長すれば保たれる。故に s = −1 を代入して −3ζ(−1) = η(−1) を得るが、このイータ関数はこの級数を定義するアーベル和に等しいから η(−1) は容易に計算できる[15]。つまり、片側極限
が求まって、両辺を −3 で割れば、ζ(−1) = −1/12 を得る。
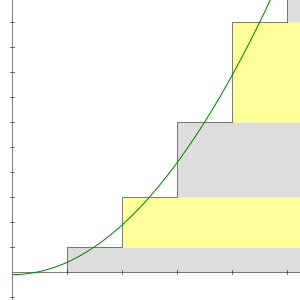
平滑化漸近線
[編集]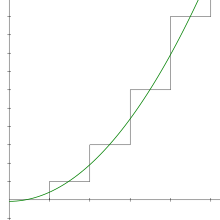
テレンス・タオは級数の平滑化によって −1/12 が得られることを指摘している。平滑化はゼータ関数正規化(複素解析を背景とする)とラマヌジャン総和法(オイラー=マクローリンの公式の便法)とを概念的に橋渡しするものである。これは、保守的な級数変化法を直接操作する代わりに、実解析の方法論を用いるのである。
この考えは、素性の悪い (ill-behaved) 離散的級数 を、よい性質 (well-behaved) のカットオフ関数 f を用いて、その滑らかな変形版 で置き換える。このカットオフ関数は f(0) = 1 に正規化されていなければならない[注釈 3]。カットオフ関数は級数の悪い点を滑らかにするために充分に有界な導関数を持ち、級数の増加よりも早く 0 に減少する必要がある。便宜のため、f は滑らかで有界かつ台がコンパクトであるものと仮定する。このとき、この平滑化された和が − 1/12 + CN2 に漸近することが示される(ただし C は f に依存して決まる定数)。この漸近展開の定数項は f の選び方に依らないが、これが必ずしも解析接続によって得られる値 −1/12 と同じであると決まっているわけではない[12]。
ラマヌジャン総和法
[編集]1 + 2 + 3 + 4 + … のラマヌジャン和も −1/12 になる。ハーディへ宛てたラマヌジャンの二通目の書簡 (1913年2月27日付け) には
"Dear Sir, I am very much gratified on perusing your letter of the 8th February 1913. I was expecting a reply from you similar to the one which a Mathematics Professor at London wrote asking me to study carefully Bromwich's Infinite Series and not fall into the pitfalls of divergent series. … I told him that the sum of an infinite number of terms of the series: 1 + 2 + 3 + 4 + … = −1/12 under my theory. If I tell you this you will at once point out to me the lunatic asylum as my goal. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter. …"[16]
と書かれている。
ラマヌジャン総和法は、級数の部分和に対するオイラー=マクローリンの公式の定数項だけを分離する方法である。関数 f に対して、級数 の古典ラマヌジャン和 (classical Ramanujan sum) は
で定義される。ここで f (2k−1) は f の (2k − 1)-階導関数で B2k は 2k-番目のベルヌーイ数である (B2 = 1/6, B4 = −1/30, ……)。 f(x) = x とすれば f の一階導関数が f (1) = 1 で残りはすべて消えるから、
を得る[17]。
矛盾が起きるのを避けるため、ラマヌジャン総和法の現代的理論では、f の高階導関数が「オイラー=マクローリンの公式の剰余項が 0 に収束するのに充分な速さで減少する」という意味の「正則性」を持つことを要求する。ラマヌジャンはこの性質を暗に仮定している[17]。この正則性を課すことによって、そのような正則な関数をとることができない 0 + 2 + 0 + 4 + … のような病的な級数にラマヌジャン総和法が適用されることは防げる。そのような級数について、ラマヌジャン和の代わりにゼータ関数正規化によって解釈されるべきである。この理由を以ってハーディは、既知の級数のラマヌジャン和を関連する級数の和を求めるのに用いるときには「厳重な注意」("great caution") を要すると述べた[18]。
物理学での応用
[編集]ボゾン弦理論では、弦の取り得るエネルギー準位、とくに最低エネルギー準位を計算することが試みられる。砕けた言い方をすると、時空の次元を D とするとき、弦の振動は D − 2 個の独立な量子調和振動子(各々は横波)の集まりと見ることができて、基本振動数、すなわち弦の振動数の中で最も小さいものを ν とすると振動子のエネルギーにおける n 番目の振動子の寄与は hνn/2 と表せるので[注釈 4]、件の級数を用いれば全ての振動数に亘る和を計算すると −hν(D − 2)/24 が得られる。最終的には、この事実にゴダード・ソーンの定理を合わせて、ボゾン弦理論が 26 次元でないと無矛盾にならないことが導かれる。また、これに超対称性を取り入れた超弦理論は9次元(+時間1次元で計10次元)において無矛盾であることが示される。
級数 1 + 2 + 3 + 4 + … の計算は一次元のスカラー場に対するカシミール力の計算にも関わってくる。指数的カットオフ関数は級数を滑らかにするのに充分で、これは高エネルギー状態が導電性板によってブロックされないという事実を表している。この問題の空間対称性はこの展開の二次の項がキャンセルされることの原因である。残るのは定数項 −1/12 であるが、この負符号はカシミール力が吸引力であるという事実を反映している[19]。
同様の計算は 3 次元でも存在し、リーマンゼータの代わりにエプスタインゼータが用いられる[20]。
メディアでの扱い
[編集]デーヴィッド・リーヴィットの小説 The Indian Clerk には、ハーディとリトルウッドがこの級数について議論するシーンが出てくる[21]。サイモン・マクバーニーの2007年の作品 A Disappearing Number では舞台の冒頭でこの級数が取り上げられている[22]。
2014年1月9日、YouTube の番組 Numberphile でこの級数に関する動画が投稿され[23]、公開から1ヶ月間で 150 万以上の再生数を獲得した[24]。動画は 8 分間でノッティンガム大学の物理学者、トニー・パディーヤが解説をしている。パディーヤは S1 = 1 − 1 + 1 − 1 + … と S2 = 1 − 2 + 3 − 4 + … から始め、最後に S = 1 + 2 + 3 + 4 + … を、ラマヌジャンの議論と同様に項別の引き算を用いてそれらの級数の関連性を述べている。Numberphile はノッティンガム大学の物理学者、エド・コープランドを招いた 21 分の動画も制作しており、アーベル和として S2 = 1 − 2 + 3 − 4 + … = 1/4 となること、ζ(−1) として S = 1 + 2 + 3 + 4 + … = −1/12 となることについて、より詳細に解説している[25] 。 後日、最初の動画が厳密性に欠けているという批判があり、パディーヤは彼のウェブページで、動画の中で行った操作と実際に行われている relevant なディリクレ級数に対する解析接続との関係についての解説を書いている[26]。 ニューヨーク・タイムズの Numberphile の動画に関する記事で、数学者のエドワード・フレンケルは次のようにコメントしている[24]。「この計算は数学界における最高の秘密の一つだろう。外部の人間は誰もそれについて知らないのだ 」。
脚注
[編集]注釈
[編集]- ^ 数を関数に昇華して考えることは、二つの広汎な総和法のクラスの、アーベル総和法やボレル総和法などを含む一派として理解することができる[13]。
- ^ より一般に、ζ(s) の値は ∑∞
n=1 n−sehn の h = 0 の周りでのローラン展開の定数項として常に与えられる。 - ^ これは微分方程式において用いられる正規化とは異なる
- ^ h はプランク定数。振動数 ν の逆数はその振動の周期 τ を表し、振動数と周期の積は ντ = 1 である。振動数に似たものに角振動数 ω があり、角振動数と振動数の間には ω = 2πν という関係がある。三角関数の周期は 2π であるため、物理学の文献では振動数でなく角振動数が好んで用いられる。それに合わせてプランク定数 h を 2π で割った換算プランク定数(ディラック定数)ħ ≔ h/2π がしばしば用いられる。ν, h および ω, ħ の積は互いに等しい (hν = ħω)。
出典
[編集]- ^ Lepowsky 1999, pp. 327–340.
- ^ “数学ノート 1+2+3+4+…=-1/12(シーズン2)”. NHK. 2024年9月12日閲覧。
- ^ Gannon 2010, p. 140.
- ^ Pengelley 2002, p. 3.
- ^ Carl,Erickson(2005),A Geometric Perspective on the Riemann Zeta Function's Partial Sums
- ^ “関数の拡張と1+2+3+4+5+...=-1/12 の謎|きいねく|note”. note. 2021年12月7日閲覧。
- ^ Hardy 1949, p. 10.
- ^ ラマヌジャンのノート第 1 巻 8 章
- ^ Abdi 1992, p. 41.
- ^ Berndt 1985, pp. 135–136.
- ^ Euler 1768, pp. 83–106.
- ^ a b c Tao 2010.
- ^ Knopp 1990, pp. 475–476.
- ^ Stopple 2003, p. 202.
- ^ Knopp 1990, pp. 490–492.
- ^ Berndt et al. p. 53.
- ^ a b Berndt 1985, pp. 13, 134.
- ^ Hardy 1949, p. 346.
- ^ Zee 2003, pp. 65–67.
- ^ Zeidler 2007, pp. 305–306.
- ^ Leavitt 2007, pp. 61–62.
- ^ Thomas 2008.
- ^ ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12 - YouTube
- ^ a b Overbye, Dennis (February 3, 2014), “In the End, It All Adds Up to – 1/12”, New York TImes February 3, 2014閲覧。
- ^ Sum of Natural Numbers (second proof and extra footage) - YouTube
- ^ Padilla, Tony, What do we get if we sum all the natural numbers? February 3, 2014閲覧。
参考文献
[編集]- 数学関連
- Lepowsky, J. (1999). "Vertex operator algebras and the zeta function". In Naihuan Jing and Kailash C. Misra (ed.). Recent Developments in Quantum Affine Algebras and Related Topics. Contemporary Mathematics. Vol. 248. pp. 327–340. arXiv:math/9909178。
- Gannon, Terry (April 2010), Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms and Physics, Cambridge University Press, p. 140
- Pengelley, David J. (2002). "The bridge between the continuous and the discrete via original sources". In Otto Bekken; et al. (eds.). Study the Masters: The Abel-Fauvel Conference. National Center for Mathematics Education, University of Gothenburg, Sweden. p. 3.
- Ramanujan, S., Ramanujan's Notebooks January 26, 2014閲覧。
- Abdi, Wazir Hasan (1992), Toils and triumphs of Srinivasa Ramanujan, the man and the mathematician, National, p. 41
- Berndt, Bruce C. (1985), Ramanujan’s Notebooks: Part 1, Springer-Verlag, pp. 135–136
- Berndt, Bruce C., Srinivasa Ramanujan Aiyangar, and Robert A. Rankin (1995). Ramanujan: letters and commentary. American Mathematical Society. ISBN 0-8218-0287-9
- Hardy, G.H. (1949). Divergent Series. Clarendon Press. LCC QA295 .H29 1967
- Euler, Leonhard (1768). “Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques”. Memoires de l'academie des sciences de Berlin 17: 83–106.
- 翻訳:Euler, Leonhard; Lucas Willis; and Thomas J Osler (2006年). “Transl ation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series”. The Euler Archive. 2007年3月22日閲覧。
- Knopp, Konrad (1990) [1922]. Theory and Application of Infinite Series. Dover. ISBN 0-486-66165-2
- Stopple, Jeffrey (2003), A Primer of Analytic Number Theory: From Pythagoras to Riemann, p. 202, ISBN 0-521-81309-3
- Tao, Terence (April 10, 2010), The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation January 30, 2014閲覧。
- 物理学関連
- Zee, A. (2003). Quantum field theory in a nutshell. Princeton UP. ISBN 0-691-01019-6
- Zeidler, Eberhard (2007), Quantum Field Theory I: Basics in Mathematics and Physics: A Bridge between Mathematicians and Physicists, Springer, pp. 305–306, ISBN 9783540347644
- 一般書・小説
- Leavitt, David (2007), The Indian Clerk, Bloomsbury, pp. 61–62
- Thomas, Rachel (December 1, 2008), “A disappearing number”, Plus February 5, 2014閲覧。
関連文献
[編集]- Lepowsky, James (1999). “Vertex operator algebras and the zeta function”. Contemporary Mathematics 248: 327–340. arXiv:math/9909178.
- Zwiebach, Barton (2004). A First Course in String Theory. Cambridge UP. ISBN 0-521-83143-1 See p. 293.
- Kaneko, Masanobu; Kurokawa, Nobushige; Wakayama, Masato (2003), “A variation of Euler's approach to values of the Riemann zeta function”, Kyushu Journal of Mathematics (九州大学大学院数理学研究院) 57 (1): 175–192, arXiv:0206171, doi:10.2206/kyushujm.57.175, hdl:2324/11683 2023年9月26日閲覧。
- Elizalde, Emilio (2004). "Cosmology: Techniques and Applications". Proceedings of the II International Conference on Fundamental Interactions. arXiv:gr-qc/0409076。
- Watson, G. N. (April 1929), “Theorems stated by Ramanujan (VIII): Theorems on Divergent Series”, Journal of the London Mathematical Society, 1 4 (2): 82–86, doi:10.1112/jlms/s1-4.14.82
外部リンク
[編集]- This Week's Finds in Mathematical Physics (Week 124), (Week 126), (Week 147), (Week 213)
- Euler’s Proof That 1 + 2 + 3 + · · · = −1/12 - By John Baez
- John Baez (September 19, 2008). “My Favorite Numbers: 24”. 2010年4月22日閲覧。
- The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation by Terence Tao
- A recursive evaluation of zeta of negative integers by Luboš Motl
- Sum of Natural Numbers (second proof and extra footage) オイラーの方法の解説がある。
- What do we get if we sum all the natural numbers? response to comments about video by Tony Padilla
- Related article from New York TImes
- Divergent Series: why 1 + 2 + 3 + · · · = −1/12 アリゾナ大学の Brydon Cais による