極小曲面

ヘリカルフレーム上の石鹸膜によって形成されるヘリコイド極小曲面

数学または物理学において、極小曲面（きょくしょうきょくめん、英: minimal surface）とは局所的にその面積を最小化する曲面である。

これは平均曲率（英語: mean curvature）が零をもつことと同じである（以下の定義を見よ）。

解説

「極小曲面」の用語はこれら曲面が本来ある一定の面積を合計として最小にする曲面としてであるから用いられる。極小曲面の面積を最小化する物理的モデルは、石鹸膜（英語: soap film）が生じる、石鹸液に針金の枠を漬けることで作ることができる。それはその針金枠を境界とする極小曲面である。しかしながら、その用語は自己交差や制約されないより一般的な曲面についても用いられる。そこで与えられた制約条件は面積の異なる幾つかの極小曲面をも成り立たせる（例えば、回転極小曲面（英語: minimal surface of revolution） を見よ）：標準的な定義は局所的最適に関係するだけで、大域的最適ではない。

定義

鞍塔状極小曲面、その面積を増加させる曲面の任意の小さな変形のなかで、最も小さな合計面積をもつ同じ境界である曲面が存在する。

極小曲面は$\mathbb {R} ^{3}$において、幾つかの同値な方法により定義できる。それらが同値である事実は極小曲面の理論がいかに幾つもの数学上の分野にまたがっているかを示す、とりわけ微分幾何学、変分法、ポテンシャル論、複素解析そして数理物理学。

局所最小面積定義（英: local least area definition）：おなじ境界をもつすべての曲面のうち最小の面積をもつ、単純閉曲線により境界づけられた、曲面$M\subset \mathbb {R} ^{3}$は、任意の点 p ∈ Mが近傍をもてば、そのときに限り極小である。

この性質は局所的である：より小さな面積のおなじ境界をもつその他の曲面とともに、極小曲面では領域が存在しなければならない。この性質は石鹸膜に関連して確立された；境界としての針金枠に、極小の面積になるよう石鹸膜は形作られる。

変分的定義（英: variational definition）：曲面$M\subset \mathbb {R} ^{3}$は、コンパクトに支持されたすべての変分に対する面積関数の臨界点であれば、そのときに限り極小である。

この定義は、長さ関数の臨界点として類似に定義されるものである、測地線に対する2次元の類似として極小曲面を成り立たせる。

極小曲面の曲率平面。極小曲面では、主曲率の平面のうちの曲率は同じであり、すべての点で正負が逆である。これは主曲率が零であることを意味する。

平均曲率的定義（英: mean curvature definition）：曲面$M\subset \mathbb {R} ^{3}$は、すべての点でその平均曲率 （英語: mean curvature）が零に等しければそのときに限り極小である。

この定義の直接な意味は、曲面上の任意の点は等しくかつ相対する主曲率の鞍点であるということである。さらに言えば、これは、極小曲面が平均曲率流れ （英語: mean curvature flow）の静的な解を与えることを示す。ヤング・ラプラスの式により、石鹸膜の平均曲率はその側面の圧力差に比例する。もしある領域で石鹸膜が囲まれていなければ、そのときこれはその平均曲率が零になることを成り立たせる。

微分方程式による定義（英: Differential equation definition）:曲面$M\subset \mathbb {R} ^{3}$はもしそれが次式の解のグラフとして局所的に表されるならばそのときに限り極小である：

$(1+u_{x}^{2})u_{yy}-2u_{x}u_{y}u_{xy}+(1+u_{y}^{2})u_{xx}=0$

この定義のその偏微分方程式はもともと1762年にラグランジュにより見つけられた、そしてジャン＝バティスト・ムーニエは1776年に平均曲率が消えることを意味していることを見出した。

エネルギーによる定義（英: energy definition）：ある等角なはめ込み$X:M\rightarrow \mathbb {R} ^{3}$は、もしすべての支持するコンパクトな多様体についてのディリクレエネルギーの臨界点であるならばそのときに限り極小である。または同値として、もし任意の点$p\in M$が、その境界に比例した最小のエネルギーをもつ近傍をもてば極小である。

この定義は極小曲面を調和関数とポテンシャル論とに結び付ける。

調和的定義（英: harmonic definition）：もし$X=(x_{1},x_{2},x_{3}):M\rightarrow \mathbb {R} ^{3}$が、あるリーマン面の3次元空間への等長的はめこみならば、$x_{i}$が各$i$の$M$における調和関数であるときはいつでも、$X$は極小であるという。

この定義と調和関数の最大値原理の直接的な意味は、$\mathbb {R} ^{3}$にはコンパクトで完備な極小曲面は無いことである。

ガウス写像による定義（英: Gauss map definition）：ある曲面$M\subset \mathbb {R} ^{3}$は、ステレオな投影であるガウス写像$g:M\rightarrow \mathbb {C} \cup {\infty }$が、もととなるリーマン面の構造に関して有理型であり、かつ'球面の一部'（英: piece of a sphere）ではないときに限り極小である。

この定義は、そのガウス写像のその導関数と関係する、平均曲率が形状作用素の跡の半分であることを用いる。もし投影されたガウス写像がコーシー・リーマン方程式に従うならば、この場合それは球面の一部であって、跡は消えるかまたは$M$の各点は臍点（英語: umbilical point）である。

局所最小面積定義と変分的定義は$\mathbb {R} ^{3}$よりも高次のリーマン多様体へ拡張して定義することを極小曲面に与える。

歴史

極小曲面の理論は ラグランジュが1762年に、与えられた閉じた輪郭に交差して引き伸ばされる最小の面積の曲面$z=z(x,y)$を探す変分問題を考えたときに始まる。 彼はその解に対して次のオイラー＝ラグランジュ方程式を導いた：

${\frac {d}{dx}}\left({\frac {z_{x}}{\sqrt {1+z_{x}^{2}+z_{y}^{2}}}}\right)+{\frac {d}{dy}}\left({\frac {z_{y}}{\sqrt {1+z_{x}^{2}+z_{y}^{2}}}}\right)=0$

彼は平面以外に何らの解も見つけることにはならなかった。1776年にジャン＝バティスト・ムーニエは螺旋面 （英語: Helicoid）と懸垂面 （英語: catenoid ）がその方程式を満たすこと、および微分の表現がその曲面の平均曲率 （英語: mean curvature ）の二倍に関係すること、結論として零平均曲率をもつ曲面は面積極小であることを見出した。

ラグランジュの方程式を次のように拡張することによって：

$\left(1+z_{x}^{2}\right)z_{yy}-2z_{x}z_{y}z_{xy}+\left(1+z_{y}^{2}\right)z_{xx}=0$

ガスパール・モンジュとアドリアン＝マリ・ルジャンドルは1795年に解の曲面についての式の表現を導いた。ハインリッヒ・シャーク（英語: Heinrich Scherk）が1830年に彼の曲面を導いたことによってこれらが成功したときに、彼らは実際には役立たないものとして一般的に見なした。ウジェーヌ・シャルル・カタランは1842年と1843年に螺旋面が唯一の線織面 （英語: ruled surface）の極小曲面であることを証明した。

'複素解析の方法'（英: complex method）によりビョーリング問題（英語: Björling problem）が解かれた、その世紀の半ばまで明らかに進歩は低下した。しかし極小曲面の「最初の黄金時代」は始まった。シュワルツは複素解析の方法によりプラトー問題 （英語: Plateau's problem ）の正四角形についての解を1865年に、そして一般の四角形について（彼の周期的シュワルツ極小曲面 （英語: Schwarz minimal surface）の構成により）1867年に見出した。ワイエルシュトラスとアルフレッド・エネパー （英語: Alfred Enneper ）は、極小曲面を複素解析と調和関数とに強固に結びつける、もっと便利なワイエルシュトラス-エネパー媒介変数表示 （英語: Weierstrass–Enneper parameterization ）を開発した。他の重要な寄与はベルトラミ、ボネ、ダルブー、リー、リーマン、セレ、ワインガルテンからあった。

1925年から1950年にかけて、極小曲面の理論は復活した、今では主に'非媒介変数表示極小曲面'（英: nonparametric minimal surface）が指向されている。ジェス・ダグラスとチボー・ラド（英語: Tibor Radó）によるプラトー問題の完全な解決は主な金字塔である。バーンスタイン問題（英語: Bernstein's problem）と'有限総曲率'（英: finite total curvature ）の'完備極小曲面'（英: complete minimal surface）に関するロバート・オサーマン（英語: Robert Osserman）の業績も重要である。

またの復活が1980年代に始まった。一つの契機は1982年のセルソ・コスタによるある曲面の発見である。これは、平面、懸垂面、螺旋面だけが有限な位相的な型の$\mathbb {R} ^{3}$ で完全に埋め込まれた極小曲面であることの予想を証明するものである。これは古い媒介変数的方法を用いた新しい成果を刺激するのみならず、研究された曲面を可視化するコンピューターグラフィックスと（大きな対称な曲面へ組み入れることができる、曲面の'切れ端'（英: patch）を決める、随伴曲面法を用いるときに、一定の媒介変数ははめ込まれる曲面をつくるよう数値的に適合することが必要になる）「区間問題（英: period problem）」を解く数値的方法の重要性を示した。別の契機はH.カルチャー（英: H. Karcher）による証明である。これはもともと1970年にアラン・ショーンによって経験的に述べられた3重周期極小曲面（英語: Triply periodic minimal surface）が実在することである。これは有意義な曲面の族と、古い曲面から例えばそれらに把手（とって、英: handle）を付けたり捻じ曲げたりすることで、新しい曲面を派生する方法を導き出した。

現状では、極小曲面の理論は取巻く他の幾何学における極小部分多様体の理論に多様化して、数理物理学（例えば、正値エネルギー理論 （英語: positive energy theorem）、リーマン・ペンローズ不等式 （英語: Riemannian Penrose inequality ））と三次元多様体の幾何学（例えば、スミス予想 （英語: Smith conjecture）、ポアンカレ予想、幾何化予想）に関係するようになった。

例

螺旋面。

懸垂面から螺旋面への、全点での等長な局所変換。

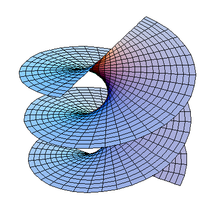
極小曲面の古典的な具体例は以下を含む：

• 自明な場合として、平面
• 懸垂面 （英語: catenoid）：懸垂線をその回転軸に1周して作られる極小曲面
• 螺旋面 （英語: helicoid ）：その直線に垂直なひとつの回転軸のまわりに一定の速度で回転しながら、一定の速度をもって回転軸に沿って同時に進む直線によって描かれる曲面

懸垂面と螺旋面は、一方から他方への連続変形があることを与えられるという特筆に価する性質を有する。その局所的な変形はすべての点において等長である。加えて、変形途中のすべての曲面は極小曲面である。これらについて、懸垂面を表す変数値0から螺旋面を表す変数値${\frac {\pi }{2}}$までの、$t$を変形の媒介変数として、そして次に示す$t$からの変形途中の曲面を表す変数の$(u,v)$である、媒介変数表示を私たちは容易に得る：

$x={\frac {e^{u}\cos(v-t)}{2}}+{\frac {e^{-u}\cos(v+t)}{2}}$

$y={\frac {e^{u}\sin(v-t)}{2}}+{\frac {e^{-u}\sin(v+t)}{2}}$

$z=u\cos(t)+v\sin(t)$

19世紀の黄金時代からの曲面は以下を含む：

• シュワルツの極小曲面 （英語: Schwarz minimal surface ）：

$\mathbb {R} ^{3}$を埋める三重周期極小曲面 （英語: Triply periodic minimal surface ）

• リーマンの極小曲面 （英語: Riemann's minimal surface ）：没後説明された周期的曲面
• エンネパー曲面
• ヘネバーグ曲面 （英語: Henneberg surface ）：最初に見出された向き付け不可能な極小曲面
• ボーアの極小曲面 （英語: Bour's minimal surface ）：自己交差する極小曲面
• ネオビウス曲面 （英語: Neovius surface ）：三重周期曲面

コスタの極小曲面 （英語: Costa's Minimal Surface）

現代の曲面は以下を含む：

• ジャイロイド：液晶構造にとくに関係する三重曲面の、1970年以来のシェーンの曲面のひとつ。
• 鞍型塔状曲面 （英語: saddle tower ）の族：シャークの第二曲面 （英語: Scherk surface#Scherk's second surface ）の一般化
• コスタの極小曲面 （英語: Costa's minimal surface ）：著名な未証明の定理。セルソ・コスタ （英語: Celso Costa）と後に視覚化したジェームズ・ホフマン （英語: James Hoffman ）による。ジェームズ・ホフマン、ダビド・ホフマンおよびウィリアム・ミークス3世はそのとき異なった回転対称をもつ曲面の族を導く定義を拡張した。
• エンネパー曲面に把手を付けた、チェン‐ガクスタッター曲面 （英語: Chen–Gackstatter surface ）の族

零でない一定のある曲率をもつ、球面は、用語の規定の意味において極小曲面ではない。それは別の極小の意味においてであることを確かめられる：それは一定の体積を内包して面積が極小である曲面である（等周定理の項を見よ）。

数学的性質

偏微分方程式

$\mathbb {R} ^{3}$に横たわる或る曲面は、二変数$u$と$v$からなる或る関数のグラフの如き表現である（ユークリッド）座標の変換により、局所化を与えられる。詳しくは、その曲面は座標の点の組み合わせに分解される：

${\vec {M}}={\begin{pmatrix}u\\v\\f(u,v)\end{pmatrix}}$,

記法${\frac {\partial f}{\partial u}}=f_{u}$と${\frac {\partial ^{2}f}{\partial u^{2}}}=f_{uu}$を用いて、オイラー-ラグランジュによる局所的方程式に書き直される：

$f_{uu}(1+f_{v}^{2})-2f_{u}f_{v}f_{uv}+f_{vv}(1+f_{u}^{2})=0.$

この方程式は一次と二次の階数の$f$のその偏微分を導く証拠とよばれる或る関係を示す：これは偏微分方程式の一例である。

例：式$z=f(v/u)$の解による唯一の族は螺旋面（フランス語: hélicoïde）である。式$z=f(u)+g(v)$の解による唯一の族はシャーク曲面 （フランス語: Surfaces de Scherk ）である。

• 同様にもしそれらが反‐直観的に思われるのを与えるならば、それはプラトー問題の解の唯一性が存在しない。言い換えれば、それは単独の極小曲面が与えれられた条件では定まらないことを示す。すなわち'輪郭'（仏: contour）に対する極小曲面の個数に関して如何なるものかである：
  • もし輪郭が或る平面曲線であるならば、それは或る極小曲面を囲む。同様にしてもしそれが或る平面への単なる射影であるならば或る凸状曲線に沿う（Rado,1932）。
  • 曲率の合計が$4\pi$以下である曲線は円盤状の極小曲面の'境界'（仏: border）を与える。
  • 解析的曲線（仏: courbe analytique）は、有限の個数の、面積が極小である曲面の境界を与える。

モース理論の応用

モース理論は、臨界点の計算についての有効性を十分に上げる；有限次元のコンパクト空間において定義された或る関数の臨界点の個数を評価するのを含めて成し遂げるところの、モース不等式をもつことでそれは有名である。曲率が零の曲面は面積あるいは体積の臨界点として呈する。それはモース理論の応用を試みられる：とかくするうちに、曲面における'変分'（仏: variation）は無限次元での検討の必要性を導く。コンパクト性は基本的な位相の性質において依存していることを与えない。

それでも、類似の理論が成り立ち恒等式を与える：

$(-1)^{Y_{1}}+(-1)^{Y_{2}}+...+(-1)^{Y_{n}}=1,$

ここで$n$は異なる極小曲面の個数であり、すべての$Y_{n}$は、極小曲面毎に関係する特性数である。

一般化と他分野との関係

極小曲面は$\mathbb {R} ^{3}$以上の、双曲空間 （英語: hyperbolic space ）、高次元空間、またはリーマン多様体のような、他の多様体でも定義できる。

極小曲面の定義は定曲率曲面 （英語: Constant-mean-curvature surface）に一般化または拡張できる：必ずしも零である必要はない、平均曲率を有する曲面。

等温曲面（英: isothermal surface）の曲率線（英: curvature line）は等温網（英: isothermal net）を成す。

離散微分幾何学 （英語: discrete differential geometry ）では離散極小曲面が研究される：頂点の位置の'微動'（英: small perturbation ）のもとで面積を最小化する三角形による複体。そのような離散化はしばしば、閉じた表現が知られていない表示においても、数値的に極小曲面を近似するのに用いられる。

極小曲面上のブラウン運動は、極小曲面に関する幾つかの定理の、確率論的な証明を導出する。

合成物の素材の自己集合での予想された応用により、特に分子工学と材料工学の分野で、極小曲面は甚だしい科学の研究の一分野になった。細胞生物学で重要な構造の、小胞体は、非自明な極小曲面に従う進化の圧力のもとにおかれるよう提案された。

一般相対性理論とローレンツ幾何学では、みかけの地平線 （英語: apparent horizon ）として知られる、極小曲面の概念の確かな拡張と修正はは顕著である。事象の地平線と対照的に、それらはブラックホールの境界の理解への曲率に基づいた接近法を示す。

極小曲面に近似の、サーカスのテント。

テントのように、極小曲面による構造は用いられる。

極小曲面は現代のデザイナーによって用いられる生成的デザイン （英語: generative design ）の道具箱の一部である。建築においては、極小曲面に大いに関係する張力構造において多大な興味をもたれてきた。フライ・オットー、坂茂、ザハ・ハディッドの仕事において著名な事例がみられる。フライ・オットーによるミュンヘン・オリンピック競技場の計画は石鹸膜に着想を得ているさらにフライ・オットーによる別の著名な事例は、カナダのモントリオールの1967年万博でのドイツ館である。

美術界ではとりわけ、ロバート・エグマン （英語: Robert Engman ）（ 1927 - 2018 ）、ロバート・ロングハースト （英語: Robert Longhurst ）（ 1949 - ）、およびチャールズ・O・ペリー （英語: Charles O. Perry ）（ 1929 - 2011 ）の彫塑において、極小曲面は発展的に開花してきた。

関連項目

• Surface Evolver （英語: Surface Evolver ）
• ウィア＝フェラン構造
• エネパー-ワイエルシュトラス媒介変数化 （英語: Weierstrass–Enneper parameterization ）
• 曲率
• 三重周期極小曲面 （英語: triply periodic minimal surface ）
• シャボン玉
• シュワルツ極小曲面 （英語: Schwarz minimal surface ）
• 伸張格子法 （英語: stretched grid method ）
• 双線形補間 （英語: bilinear interpolation ）
• 調和写像 （英語: harmonic map ）
• 調和同型 （英語: harmonic morphism ）
• 張力構造
• バーンスタインの問題 （英語: Bernstein's problem ）
• プラトー問題 （英語: Plateau's problem ）
• ブリヤン曲面 （英語: Bryant surface ）

脚注または引用文献

ウェブサイト

• “Isothermal surface - Encyclopedia of Mathematics”. encyclopediaofmath.org (2011年). 2022年9月4日閲覧。
• “AD Classics: Olympiastadion (Munich Olympic Stadium) / Behnisch and Partners & Frei Otto” (英語). ArchDaily (2011年2月11日). 2022年9月4日閲覧。
• “Expo 67 German Pavilion”. Architectuu. 2022年9月4日閲覧。

書籍

• Choquet-Bruhat, Yvonne (2009). General relativity and the Einstein equations. Oxford Mathematical Monographs. Oxford: Oxford University Press. ISBN 978-0-19-923072-3. xxvi+785 pp. 

雑誌

• Lagrange, J. L. (1760). “Essai d'une nouvelle methode pour determiner les maxima et les minima des formules integrales indefinies”. Miscellanea Taurinensia 2 325 (1): 173 ,199. 
• Meusnier, J. B. (1785). “Mémoire sur la courbure des surfaces”. Mém. Mathém. Phys. Acad. Sci. (Paris, prés. par div. Savans) (10): 477–510, Presented in 1776. 
• Pinkall, Ulrich; Polthier, Konrad (1993). “Computing Discrete Minimal Surfaces and Their Conjugates”. Experimental Mathematics 2 (1): 15–36. doi:10.1080/10586458.1993.10504266. MR1246481. http://projecteuclid.org/euclid.em/1062620735. 
• Neel, Robert (2009). “A martingale approach to minimal surfaces”. Journal of Functional Analysis 256 (8): 2440–2472. arXiv:0805.0556. doi:10.1016/j.jfa.2008.06.033. MR2502522. 
• Meeks, William H. III; Pérez, Joaquín (2011). “The classical theory of minimal surfaces”. Bull. Amer. Math. Soc. 48 (3): 325–407. doi:10.1090/s0273-0979-2011-01334-9. MR2801776. 
• Terasaki, Mark; Shemesh, Tom; Kasthuri, Narayanan; Klemm, Robin W.; Schalek, Richard; Hayworth, Kenneth J.; Hand, Arthur R.; Yankova, Maya et al. (2013-07-18). “Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs”. Cell 154 (2): 285–296. doi:10.1016/j.cell.2013.06.031. ISSN 0092-8674. PMC 3767119. PMID 23870120. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3767119/. 
• Han, Lu; Che, Shunai (April 2018). “An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems” (英語). Advanced Materials 30 (17): 1705708. Bibcode: 2018AdM....3005708H. doi:10.1002/adma.201705708. PMID 29543352. https://onlinelibrary.wiley.com/doi/10.1002/adma.201705708. 

参考文献

• Pierre-Gilles de Gennes ; Françoise Brochard-Wyart ; David Quéré (2002) (フランス語). Gouttes, bulles, perles et ondes. Échelles. Paris: Belin. ISBN 2701140552 
• Berger, Marcel (2003) (英語). A Panoramic View of Riemannian Geometry. Berlin: Springer Verlag. pp. xxiv + 824. ISBN 978-3-540-65317-2 
• Sylvestre Gallot; Dominique Hulin; Jacques Lafontaine (2004) (英語). Riemannian Geometry (3rd. ed.). Springer-Verlag - Universitext. ISBN 978-3-540-20493-0 

教科書

• R. Courant. Dirichlet's Principle, Conformal Mapping, and Minimal Surfaces. Appendix by M. Schiffer. Interscience Publishers, Inc., New York, N.Y., 1950. xiii+330 pp.
• H. Blaine Lawson, Jr. Lectures on minimal submanifolds. Vol. I. Second edition. Mathematics Lecture Series, 9. Publish or Perish, Inc., Wilmington, Del., 1980. iv+178 pp. ISBN 0-914098-18-7
• Robert Osserman. A survey of minimal surfaces. Second edition. Dover Publications, Inc., New York, 1986. vi+207 pp. ISBN 0-486-64998-9, MR0852409
• Johannes C.C. Nitsche. Lectures on minimal surfaces. Vol. 1. Introduction, fundamentals, geometry and basic boundary value problems. Translated from the German by Jerry M. Feinberg. With a German foreword. Cambridge University Press, Cambridge, 1989. xxvi+563 pp. ISBN 0-521-24427-7
• Nishikawa, Seiki (2002). Variational problems in geometry. Translations of mathematical monographs; Iwanami series in modern mathematics. 205. Providence, R. I. : American Mathematical Society. ISBN 0821813560. ISSN 0065-9282, translated from: 

• 西川青季『幾何学的変分問題』 28巻、岩波書店、東京〈岩波講座現代数学の基礎〉、1998年1月。ISBN 4-00-010642-2。 

• Ulrich Dierkes, Stefan Hildebrandt, and Friedrich Sauvigny. Minimal surfaces. Revised and enlarged second edition. With assistance and contributions by A. Küster and R. Jakob. Grundlehren der Mathematischen Wissenschaften, 339. Springer, Heidelberg, 2010. xvi+688 pp. ISBN 978-3-642-11697-1, doi:10.1007/978-3-642-11698-8 , MR2566897
• Tobias Holck Colding and William P. Minicozzi, II. A course in minimal surfaces. Graduate Studies in Mathematics, 121. American Mathematical Society, Providence, RI, 2011. xii+313 pp. ISBN 978-0-8218-5323-8

オンライン文献

• Karcher (1995年). “Touching Soap Films - An introduction to minimal surfaces”. 2006年12月27日閲覧。 (graphical introduction to minimal surfaces and soap films.)
• Jacek Klinowski. “Periodic Minimal Surfaces Gallery”. 2009年2月2日閲覧。 (A collection of minimal surfaces with classical and modern examples)
• Martin Steffens and Christian Teitzel. “Grape Minimal Surface Library”. 2008年10月27日閲覧。 (A collection of minimal surfaces)
• Various (2000年). “EG-Models”. 2004年9月28日閲覧。 (Online journal with several published models of minimal surfaces)

外部リンク

• Hazewinkel, Michiel, ed. (2001), “Minimal surface”, Encyclopaedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://eom.springer.de/p/m063920.htm 
• 3D-XplorMath-J Homepage — Java program and applets for interactive mathematical visualisation
• Gallery of rotatable minimal surfaces
• WebGL-based Gallery of rotatable/zoomable minimal surfaces