モース理論
原文と比べた結果、この記事には多数の(または内容の大部分に影響ある)誤訳があることが判明しています。情報の利用には注意してください。 |
微分トポロジーにおいて、モース理論(モースりろん、英: Morse theory)は、多様体上の微分可能函数を研究することにより、多様体の位相的性質の分析を可能とする。マーストン・モース (Marston Morse) の基本的な見方に従うと、多様体上の典型的な微分可能函数はその位相的性質を極めて直接的に反映する。モース理論は、多様体上のCW構造やハンドル分解を見つけたり、多様体のホモロジーの本質的な情報をもたらす。
モース以前は、アーサー・ケイリー (Arthur Cayley) とジェームズ・クラーク・マクスウェル (James Clerk Maxwell) がトポグラフィーの脈絡で、モース理論のいくつかのアイデアを考え出した。モースの元来の応用は、測地線の理論(経路上のエネルギー汎函数の臨界点への応用であった。これらのテクニックは、ラウル・ボット (Raoul Bott) の周期性定理の証明に使われた。
モース理論の複素多様体での類似が、ピカール・レフシェッツ理論である。
基本概念[編集]

説明のために、山のある図形 M を考える。函数 f : M → R を M 上の各々の点を高さへ写像するとすると、R の点である等位集合の逆像は単純に等位集合(等高線)となる。各々の等高線の連結成分は、点、単純な閉曲線、または、二重点(double point)となる。等高線である輪郭線は高次の点(三重点など)となるかもしれないが、しかしこれらは不安定であり、図形の少しの変形でなくすることができるかもしれない。輪郭線の二重点は、鞍点(saddle points)や経路である。鞍点は、図形の中の曲線で一つはある方向に伸びていて、他方は別な方向へ伸びている曲線で囲まれている点を言う。
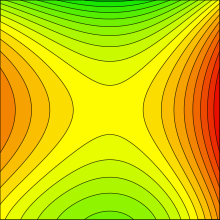
この図形の上を水に浸されていると想像すると、水が高さ a へ到達すると水でひたされている領域は、f−1(−∞, a] あるいは、高さが a よりも低い点となる。水を増やすとこの領域がどのように変化するか考えてみよう。直感的には、a が臨界点(critical point)を超えない限り変化しないように思える。すなわち、f の勾配が 0 となる点である(この点での接空間からこの点への線型写像として作用している線型写像 f のヤコビ行列が最大ランクを持たない)。言い換えると、水が下記の点に達したとき以外は、変化しない。
- (1) 水を図形に充填し始めたとき (basins)
- (2) 水位が鞍点に達したとき(峠) (passes)
- (3) 完全に図形が水没したとき (peaks)

これら 3つのタイプの臨界点 – basins, passes, と peaks (また、最小、鞍点、最大とも言う) – に対し、指数を割り付ける。直感的に言うと、周りの f が減少する独立した方向の数を、臨界点 b の指数とする。従って、最小点、鞍点、最大点の指数はそれぞれ 0, 1, 2 となる。厳密には、臨界点の指数は、その点でのヘッセ行列の負定値の部分行列の次元である。滑らかな写像の場合は、ヘッセ行列は対角行列となる。
Ma を f−1(−∞, a] と定義する。トポグラフィーの脈絡を離れ、Ma のトポロジーがどのように a の増加に対し変化するのかを、同様に分析することができる。M が向き付けられたトーラスで f が垂直軸への射影であるとき、点は平面の上の高さとなる。

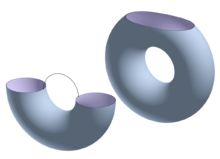
トーラスの下の端から始め、p, q, r, s を指数がそれぞれ 0, 1, 1, 2 である臨界点とする。a が 0 より小さいときは、Ma は空集合である。a が p のレベルを通り過ぎた後、0<a<f(q) のときに、Ma は、空集合に繋がる点(0-cell)にホモトピー同値な円板である。次に、a がレベル q を超えた f(q)<a<f(r) のとき、Ma は円筒状となり、(左に図示するように)1-cellである円板にホモトピー同値となる。一度 a がレベル r を超え f(r)<a<f(s) となると、Ma は消された円板を持つトーラスとなり、(右に図示するように)1-cellをもつ円筒にホモトピー同値となる。 最後に、a が臨界レベル s よりも大きくなると、Ma はトーラスとなる。もちろん、トーラスは 2-cellの円板が消された円板をもつトーラスと同じである。
従って、次のようなルールを持っているように思われる。Mα のトポロジーは、α が臨界点の高さを通る場合と指数 γ の臨界点の高さを通る場合を除き、変化しない。γ-cell は Mα に付いている。このことは、2つの臨界点が同じ高さとなったときどのようになるかについては答えてくれない。以上の状況は、f を少し摂動することにより解消することができる。図形(あるいは、ユークリッド空間へ埋め込まれた多様体)の場合には、この摂動は図形を傾ける(座標系を回転させる)というシンプルな操作になるだろう。
しかし、このルールは言い方としては誤っている。このことを理解するために、M = R で f(x) = x3 とすると、0 は f の臨界点であるが、Mα は α が 0 を通過するときに変わらない。事実、指数の考え方は意味をなさない。問題は二番目の導出である 0 でも 0 の部分である。ここでの状況の種類を、退化した臨界点という。この状況は不安定であることに注意する。座標系をグラフの下へ回転することにより、退化した臨界点は消えてしまうか、または、2つの非退化した臨界点へ分解してしまう。
形式的な拡張[編集]
微分可能多様体 M の上の実数に値を持つ滑らかな函数 f : M → R に対し、f の微分が 0 となるような点は、f の臨界点(critical points)と言われ、f による像は臨界値(critical value)と言われる。臨界点 b で 2階偏微分の行列(ヘッセ行列)が非特異ならば、b を非退化な臨界点と言い、ヘッセ行列が特異であれば、b を退化した臨界点と言う。
R から R への函数
は、b=0であれば、原点で臨界点を持つ。臨界点は c≠0(つまり、f は、a+cx2+...の形)であれば非退化であり、c=0(つまり、f は、a+dx3+...の形)であれば退化している。退化した臨界点の簡単な例が、原点で猿の鞍点(monkey saddle)となることである。
f の非退化臨界点 b の臨界指数(index)は、ヘッセ行列が負定値であるような b での M の接空間の最大部分空間の次元である。このことは、直観的な考え方である指数は f の値が減少する方向の数に対応する。退化性と臨界点の指数とは、シルベスターの慣性法則が示しているように、使用する局所座標系の選択には依存しない。
モースの補題[編集]
b を f : M → R の非退化臨界点とすると、b の近傍 U の中に近傍座標系(chart) (x1, x2, ..., xn) が存在し、すべての i に対し と
が U 全体で成り立つ。ここに α は b での f の指数に等しい。モースの補題の系として、非退化な臨界点は孤立点である。(複素領域への拡張は、複素モース補題(Complex Morse Lemma)を参照、一般化についてはモース・パレの補題(Morse-Palais lemma)を参照)
基本定理[編集]
多様体 M 上の滑らかな実数値函数は、退化した臨界点を持たないとき、モース函数(Morse function)という。モース理論の基本的結果から、ほとんどすべての函数はモース函数であることが言える。テクニカルには、モース函数の集合は、 C2位相ですべての滑らかな函数 M → R の集合の稠密な開部分集合をなすということである。このことは、「典型的な函数はモース函数である」、あるいは、「ジェネリック(generic)な函数はモース函数である」ということもある。[注釈 1]
このことを示す前に、Ma = f−1(−∞, a] のトポロジーが a の変化につれて、いつ変化するのかという問題に興味が湧く。この問題の答えの半分は次の定理によって与えられる。
- 定理: f を M 上の滑らかな実数値函数、a < b、f−1[a, b] はコンパクトで、a と b の間には臨界値が存在しないとすると、Ma は Mb は微分同相であり、Mb は Ma 上に連続縮小(deformation retract)である。
この定理は、a が臨界点を通過したとき、Ma のトポロジーがどのように変化するのかを知るためも興味がもたれる。次の定理はこの問いに対する答えである。
- 定理: f を M 上の滑らかな実数値函数、p を指数 γ である f の非退化臨界点とし、f(p) = q とする。f−1[q−ε, q+ε] はコンパクトで、p の近くには臨界点がないとすると、Mq +ε は γ-cell をもつ Mq−ε にホモトピー同値である。
これらの結果は前のセクションで述べた「ルール」を一般化し、定式化する。すでに述べたように、ルールは正しいとは言えないが、これらの定理が正しく定式化している。
2つの結果と任意の微分可能多様体上のモース函数が存在するという事実を使い、任意の微分可能多様体は指数 n の臨界点の各に対し、n-cell をもつCW複体であるということを証明することができる。証明するためには、各々の臨界レベルにひとつの臨界点を持つように整列させることができるというテクニカルな事実を必要とする。このテクニックは普通は臨界点を再整列させるため勾配的ベクトル場(gradient-like vector field)を使い証明することができる。
モース不等式[編集]
モース理論は多様体のホモロジーのいくつかの強い結果を証明することに使うことができる。f : M → R の指数 γ の臨界点の数は、f を「登る」ことから得られるCW複体の中の γ cells の数に等しい。位相空間のホモロジー群のランクの交代和は、ホモロジーが計算することのできるチェイン群のランクの交代和に等しいという事実、従って、胞体チェイン群を使い(胞体ホモロジー(英語: cellular homology)を参照)、オイラー標数 が、和
に等しいことは明らかである。ここに Cγ は指数 γ の臨界点の数である。また、胞体ホモロジーにより、CW複体 M の n-次ホモロジー群のランクは、M の n-cells の数に等しいか、または小さい。従って、γ 次ホモロジー群のランク、つまり、ベッチ数 は M のモース函数の指数 γ の臨界的の数に等しいか、または小さい。これらの事実を厳密にすることができ、モース不等式(Morse inequalities)、
を得る。
とくに、任意の
に対し、
を得る。
このことは、多様体のトポロジーを研究するための力強いツールとなる。閉じた多様体上に、ちょうど k 個の臨界点を持つモース函数 f : M → R が存在するとしてみよう。どのようにして、M へ制限した函数 f の存在を示すのであろうか? k = 2 の場合は1952年にレーブ(Reeb)により研究された。レーブの球定理(英語: Reeb sphere theorem)は M は球 に同相であることを言っている。k = 3 の場合は、おそらく、低次元の小さな数の多様体のみが可能となり、M はイールス・クーパー多様体(英語: Eells–Kuiper manifold)と同相となる。1982年にエドワード・ウィッテンは、'摂動作用素'(英: perturbed operator)についてド・ラームコホモロジーを考えることによって、モース不等式において解析的な方法を開拓した[1]。
モースホモロジー[編集]
モースホモロジー(Morse homology)は、滑らかな多様体(smooth manifold)のホモロジーを理解するためのとくに容易な方法である。モースホモロジーは、モース函数とリーマン計量を選択することにより定義する。基本定理は、結果として出てくるホモロジーは多様体の不変量である(つまり、函数と計量とは独立)という定理で、多様体の特異ホモロジーと同型となる。この定理はモースホモロジーと特異ベッチ数が一致することを意味し、モース不等式の証明となっている。モースホモロジーの無限次元の類似はフレアーホモロジーである。
エドワード・ウィッテン(Edward Witten)は、1982年に調和函数を使い、モース理論へのアプローチする別の方法を開発した。[2]
モース・ボットの理論[編集]
モース函数の考え方は、非退化臨界点しか持たない多様体上の函数を考えることへと一般化することができる。モース・ボットの函数(Morse–Bott function)は、多様体上の滑らかな函数であって、臨界点の集合は閉じた多様体であり、法線の方向にヘッセ行列が非退化である。(同じことであるが、臨界点でのヘッセ行列の核は、臨界部分多様体への接空間に等しくなる。)モース函数は、臨界多様体が 0 次元のときの特別な場合である。(従って、臨界点でのヘッセ行列はすべての方向へ非退化、つまり、核を持たない。)
指数は、非常に自然に、ペア
と考えることができる。ここに i− は、臨界多様体の与えられた点での不安定な多様体の次元であり、i+ は i− に臨界多様体の次元をプラスした次元である。モース・ボットの函数が、臨界軌跡上の小さな函数で摂動されると、摂動された函数の臨界多様体の上のすべての臨界点の指数は、i− と i+との間に存在することとなる。
モース・ボット函数は、元のモース函数が使いにくいので、役に立つ。モース・ボット函数は、可視化することができ、それを使い簡単に計算することができて、典型では対称性を持っている。それらは、正の次元の臨界モデルをもたらすことが多い。ラウル・ボット(Raoul Bott)は、モース・ボットの理論を使い、ボットの周期性定理(Bott periodicity theorem)の証明に使用した。
ラウンド函数(Round function)は、モース・ボット函数の例であり、そこでは臨界点の集合が円(非合併なユニオン)となる。
モースホモロジー(Morse homology)はモース・ボット函数の定式化でもある。モース・ボットホモロジーの微分形式は、スペクトル系列(spectral sequence)により計算される。フレデリック・ブルジェオス(Frederic Bourgeois)は、シンプレクティック場の理論のモース・ボットのバージョンでの仕事の中でアプローチしたが、非常に解析的に難しいため公開されなかった。
脚注[編集]
注釈[編集]
- ^ 「ジェネリック」なということの意味は、「ほとんどすべての」という意味である。
出典[編集]
- ^ Witten 1982、Roe 1998
- ^ Witten’s Proof of Morse Inequalities by Igor Prokhorenkov
- Roe, John (1998). Elliptic Operators, Topology and Asymptotic Method. Pitman Research Notes in Mathematics Series. 395 (2nd ed.). Longman. ISBN 0582325021
- Witten, Edward (1982). “Supersymmetry and Morse theory”. J. Differential Geom. 17 (4): 661–692. doi:10.4310/jdg/1214437492.
参考文献[編集]
- Bott, Raoul (1988). Morse Theory Indomitable. Publications Mathématiques de l'IHÉS. 68, 99–114.
- Bott, Raoul (1982). Lectures on Morse theory, old and new., Bull. Amer. Math. Soc. (N.S.) 7, no. 2, 331–358.
- Cayley, Arthur (1859). On Contour and Slope Lines. The Philosophical Magazine 18 (120), 264-268.
- Guest, Martin (2001). arXiv abstract Morse Theory in the 1990's
- Matsumoto, Yukio (2002). An Introduction to Morse Theory
- Maxwell, James Clerk (1870). On Hills and Dales. The Philosophical Magazine 40 (269), 421–427.
- Milnor, John (1963). Morse Theory. Princeton University Press. ISBN 0-691-08008-9 A classic advanced reference in mathematics and mathematical physics.
- Milnor, John (1965). Lectures on the h-Cobordism theorem - scans available here
- Morse, Marston (1934). "The Calculus of Variations in the Large", American Mathematical Society Colloquium Publication 18; New York.
- Matthias Schwarz: Morse Homology, Birkhäuser, 1993.
- Seifert, Herbert & Threlfall, William (1938). Variationsrechnung im Grossen
- Witten, Edward (1982). Supersymmetry and Morse theory. J. Differential Geom. 17 (1982), no. 4, 661–692.
関連項目[編集]
- デジタルモース理論(Digital Morse theory)
- 離散モース理論(Discrete Morse theory)
- ヤコビ集合(Jacobi set)
- ラグラジアングラスマン多様体(Lagrangian Grassmannian)
- ルスターニク・シュニレルマンカテゴリ(Lusternik–Schnirelmann category)
- モース・スメール系(Morse–Smale system)
- サードの補題
- 層化されたモース理論(Stratified Morse theory)












