ステレオ投影


ステレオ投影(ステレオとうえい、英: stereographic projection)は、球面を平面に投影する方法の一つである。ステレオ投影は複素解析学、地図学、結晶学、写真術など様々な分野で重要である。
stereographic projection の訳語は分野によって異なる。ステレオ投影は主に物理学や機械工学において用いられる。数学においては写像という意味で立体射影あるいはステレオグラフ射影、地図学では図法という意味で平射図法またはステレオ図法と呼ばれる。このように訳語が異なってはいるが、内容は全て同一視できる。
ステレオ投影は、数学的には写像として定義される。定義域は、球面から光源の一点を除いたところである。写像は滑らかかつ全単射である。また、等角写像、すなわち角度が保存される。一方、長さや面積は保存されない。これはとくに光源点付近では顕著である。
すなわち、ステレオ投影は、いくらかの避けられない妥協を含む、球面を平面に描く方法である。実際面では、コンピュータや、ウルフネットまたはステレオネットと呼ばれるグラフ用紙などを使って、投影図が描かれる。
歴史[編集]
ステレオ投影は、ヒッパルコスとクラウディオス・プトレマイオスに知られていたが、おそらくもっと早くから古代エジプトでも知られていた。これはもともと、平球投影(英語:planisphere projection[1])として知られていた[2]。プトレマイオスの著書 "Planisphaerium" は、ステレオ投影についてかかれた現存する最古の文書である。この投影の最も重要な使い方は星図を表すことであった。[2] 星座早見盤の英語 planisphere のように、今でもそのような図にこの言葉が使われる。
最初の世界地図は、1507年にグアルテリアス・ラドによって、ステレオ投影を基にそれぞれの半球を円盤に投影して描かれたと言われている[3]。ステレオ投影の赤道面への投影するという特徴は、17世紀と18世紀に東半球と西半球の地図を描くのに利用された[4]。
フランソワ・デギュイヨンが、彼の1613年の作品"Opticorum libri sex philosophis juxta ac mathematicis utiles"(哲学者と数学者に等しく役立つ6冊の光学の本)で、この投影にステレオ投影と名付けた[5]。
数学的な定義[編集]

この節では、単位球面を北極から赤道を通る平面に投影する場合を扱う。その他の場合は後述。
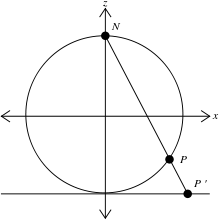
三次元空間 R3 内の単位球面は、x2 + y2 + z2 = 1 と表すことができる。ここで、点 N ≔ (0, 0, 1) を"北極"とし、M を球面の残りの部分とする。平面 z = 0 は球の中心を通る。"赤道" はこの平面と球面の交線である。
M 上の任意の点 P に対して、N と P を通る直線が一意的に存在し、この直線は平面 z = 0 とちょうど一点 P′ で交わる。P の立体射影による像を、その点 P′ と定義する。
球面上の直交座標 (x, y, z) と平面上の (X, Y) を用いると、立体射影とその逆写像は、次の式で与えられる。
球面上の球面座標 (φ, θ) と平面上の極座標 (R, Θ) を用いると、立体射影とその逆写像は
となる。ただし、R = 0 の場合は、φ = π と解釈する。
また、三角関数の等式を用いて、この式を書き直す方法がたくさんある。球面上の円柱座標 (r, θ, z) と平面上の極座標 (R, Θ) を用いると、立体射影とその逆写像は、
となる。
性質[編集]
前の節で定義された立体射影は、“南極” (0, 0, -1) を (0, 0) に、“赤道” を単位円に、南半球をその円の内側に、北半球をその円の外側に射影する。
この変換は N = (0, 0, 1) では定義されない。この点の小さい近傍は、平面の (0, 0) から遠く離れた部分集合に射影される。P を (0, 0, 1) に近づけるほど、像は (0, 0) より遠くなる。この性質により、一般に (0, 0, 1) は射影によって平面の無限遠点に写ると言われ、また球面は “無限遠点” を付け加えて平面を完備化しているといわれる。この事実が、射影幾何学や複素解析において有用である。単に位相的なレベルでは、それは球面が平面の一点コンパクト化に同相である様子を示している。


立体射影は等角写像、つまり曲線同士が互いに交わる角度を保存する(図参照)。しかし、面積は保存しない。一般に球面の領域の面積は平面に射影した面積に等しくない。XY-座標での面積要素は次のようになる:
角度と面積をともに保存する球面から平面への写像は存在しない。仮にあるとすれば、それは局所等長写像で、ガウス曲率を保存しているはずである。しかし球面と平面はガウス曲率が異なるので、これは不可能である。
立体射影の等角性は、いくつかの有用な幾何学的性質を意味する。光源点を「通らない」球面上の円は、平面上の円に射影される。光源点を「通る」球面上の円は、平面上の直線に射影される。このような直線は、無限遠点を通る円や無限大の半径を持つ円とみなされる事がある。
平面上のすべての直線は、立体射影の逆写像により球面上の円に写されると、光源点(無限遠点)で交わるようになる。平面上の平行線は、平面上では交わることはないが、球面上に投影されると光源点で接する。このように、平面上のすべての直線は、球面上のどこかで交わる—2点で横断的に交わるか、あるいは無限遠点で接するかである。(似たような性質は実射影平面でも成り立つが、交点の関係はそれとは違っている。)
球面上の等角航路を平面上に写した曲線は次の式で表される。
ここで Β は、等角航路の方位角である。よって等角航路は、等角螺旋になる。等角航路が常に子午線と同じ角度で交わるのと同じように、この螺旋は平面上の放射線(子午線の投影像)に常に同じ角度で交わる。
ウルフネット[編集]

ステレオ投影は、前節で与えたような数式を用いて、コンピューターに算出させることができる。しかし、手でグラフを描くには、これらの数式は扱いにくい。代わりに、目的に特化して設計されたグラフ用紙を使うのが一般的である。このグラフ用紙を作るには、半球上に緯線と経線の格子を置き、それらを円盤の上にステレオ投影した曲線を描く。これをステレオネットまたはウルフネットという。ウルフネットの名は、ロシア人の鉱物学者であるジョージ・ウルフ(George (Yuri Viktorovich) Wulff)[6] に由来する。
このネットの中心付近の区画と端の方の区画を比べることで、ステレオ投影の面積が歪む特性を見ることができる。この二つの区画は球面上では同じ面積を持っていた。円盤上では、端の方の区画は中心の区画の4倍近くの面積を面積を持っている。球の上の格子の目が細かければ細かいほど、その面積の比は4倍に近づく。
格子線を見ることで、この投影の正角性も見ることが出来る。球面上の緯線と経線は直角に交わるが、ウルフネット上のそれらの像も同じく直角で交わっている。
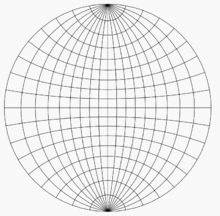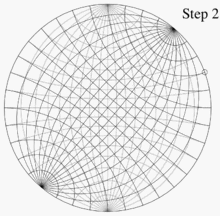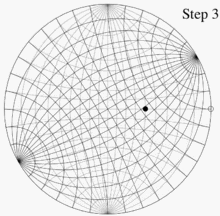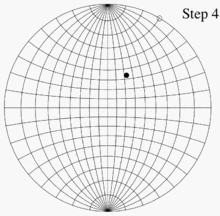
ウルフネットの使い方の例を説明する。 まずウルフネットが描かれた薄い紙を2枚用意し、片方をもう片方の上に重ね、互いの中心を揃えて鋲で止める。 仮に、下側の単位半球面上の点(0.321, 0.557, -0.766)を描くとする。この点はx軸正の方向から60° 反時計回り(またはy軸正の方向から30° 時計回り)の方向にあり、z = 0の水平面より50° 下である。これらの角度を知れば、次の4 ステップで描ける。
- ここでは格子の間隔は10° である。格子を使い、点(1, 0)から60° 反時計回り(または点(0, 1)から30° 時計回り)のネットの端に印を付ける。
- 上側のネットを回し、付けた印を下側のネットの点(1, 0)に合わせる。
- 下側の格子を使い、印を付けた点から中心に向かって50° のところに、点を打つ。
- 上側のネットをさっきとは逆方向に回し、下側のネットと揃えた元の位置に戻す。ステップ3 で打った点が、目標の点のステレオ投影である。
60° や 50° のような切りのいい数字ではない角度の点を描くには、近い格子の間を補間しなければならない。10°より目の細かいネットの方が使いやすく、格子間隔が2° のものが一般的である。
このステレオ投影点を元にして2点間の球面上の中心角を見つけるには、ウルフネットをその上に被せて、2点が同じ経線に載るまたは近くなるまで互いの中心を合わせて回す。その経線に沿って格子線を数えることで、中心角を測ることができる。
別な定式化と一般化[編集]
北極 (0, 0, 1) から南極 (0, 0, −1) における接平面 z = −1 への立体射影を定義する文献もある[7]。この射影によって得られる座標 X, Y は前記の節で記述した赤道射影 (equatorial projection) のちょうど二倍の値を与える。例えば、この射影により赤道は原点を中心とする半径 2 の円に写される。赤道射影の場合に赤道面に沿った無限小面積で歪みが無くなるのに対して、この極-接平面射影の場合では南極における無限小面積が歪んでいない。
別な文献 Gelfand, Minlos & Shapiro (1963) では半径 1/2 の球面と平面 z = −1/2 で考える。この場合の定義式は
となる。

一般に、球面上の任意の点 Q から
- E は Q を通る直径に垂直、かつ
- E は Q を含まない
という条件を満たす任意の平面 E の上への立体射影を定義することができる。E がこれら条件を満たす限りにおいて、Q でない任意の点 P に対して P, Q を通る直線と E との交わりは、P の E の上への立体射影として定義されるべき点 P′ ただ一つである[8]。
ここまでで述べた立体射影の定式化は何れも本質的に同じ性質を有する。これらは何れも射影点を除き至る所定義された滑らかな全単射(微分同相)であり、共形(等角)であって面積を保存しない。
より一般に、(n + 1)-次元ユークリッド空間 En+1 内の n-次元超球面 Sn に対して立体射影を考えることができる。Sn の点 Q と En+1 内の超平面 E に対して、点 P ∈ Sn ∖ {Q} の立体射影 P′ は直線 PQ と E との交点とする。球面上の直交座標系 (xi, i = 0, …, n) および平面上の直交座標系 (Xi, i = 1, …, n) に関して、Q = (1, 0, 0, …, 0) からの射影は
で与えられる。s2 = ∑n
j=1 Xj2 と置けば、逆写像は
となる。さらにより一般に、S を射影空間 Pn+1 内の(非特異)二次超曲面とする。つまり、S は斉次座標 xi に関する非特異二次形式 f(x0, …, xn+1) の零点の軌跡である。S 上の任意の点 Q と Q を含まない Pn+1 内の超平面 E を固定すれば、点 P ∈ S ∖ {Q} の立体射影は、直線 QP と E との唯一の交点と定められる。前と同じく、この立体射影は共形かつ「小さい」集合の外側で可逆である。この立体射影は二次超曲面を有理超曲面として与えるものである[9]。この構成は代数幾何学および共形幾何学において役割を果たす。
数学での応用[編集]
複素解析[編集]
任意の立体射影において球面上の一点(射影点)は欠けてしまうけれども、相異なる二点に関する二つの立体射影を用いれば全球を写すことができる。言葉を変えれば、球面は平面からの二つの立体図式媒介表示(立体射影の逆写像)によって被覆することができる。二つの媒介変数表示は球面上で同じ向きを持つように選ぶことができる。併せて、これらは球面を向き付けられた曲面(二次元多様体)として記述する。
この構成は複素解析において特に著しい意義を持つ。実平面上の点 (X, Y) を複素数 ζ = X + iY と同一視すれば、北極から赤道面への立体射影は
となる。同様に、別の複素座標 ξ = X − iY を取れば
が南極から赤道面への立体射影を定義する。ζ-座標から ξ-座標への遷移写像は ζ = 1⁄ξ および ξ = 1⁄ζ で与えられ、ξ → ∞ のとき ζ → 0 であり、逆もまた然りである。これにより複素数に対するエレガントで有用な無限大の概念がえられ、これは実際に有理型函数の理論の全容をリーマン球面へ引き写すものになっている。単位球面上の標準リーマン計量はリーマン球面上のフビニ–スタディ計量に一致する。
平面と直線の可視化[編集]

3次元空間の原点を通るすべての直線の集合は実射影平面と呼ばれる空間をなす。この空間は、3次元空間に埋め込む事が出来ないので、可視化するのが難しい。
しかし以下のようにして、それを円板として「ほぼ」可視化することが出来る。原点を通るすべての直線は、南半球 z ≤ 0 と交わる。その点は立体射影により円板上の点に射影することができる。水平な直線は、赤道上にある2点で南半球に交わる。そのどちらの点も、この円板に投影することができる。これに関しては、円板の境界上の対蹠点は、同一の直線を表すとして理解する(商位相空間を参照)。よって、原点を通る直線の任意の集合が、円板内の点の集合として、ほぼ完全に投影される。
また、原点を通る各々の平面は単位球面と大円(これを平面のtraceと呼ぶ)で交わる。この円は立体射影により、円に投影される。よって、この投影は、円板中の円弧として、平面を可視化することが出来る。コンピューターが普及する前には、大円のステレオ投影をするには、ビームコンパスを使って書く必要があるほど大きな半径の弧を書くことがあった。現在はコンピューターにより簡単にそれらを描くことができる。
さらに、任意の平面は、原点を通りその平面に垂直な直線を唯一つ持つ。その直線を平面の極線と呼ぶ。その直線は、その他の原点を通る直線と同様に円板の上に点を打つことができる。よって、立体射影は任意の平面も円板内の点として可視化することができる。たくさんの平面をプロットするには、平面の極線をプロットしていく方が、平面の軌跡をプロットしていくより、整然とした図を作ることができる。
この様な作業は、後で述べるように、結晶学や地学で方向のデータを可視化するのに使われる。
その他可視化[編集]

立体射影は多胞体の可視化にも使われる。シュレーゲル図では、Rn + 1 の n 次元の多胞体は、n 次元球面に射影され、それが Rn に立体射影される。Rn + 1 から Rn への低次元化は、多胞体の可視化と理解を簡単にしてくれる。
他分野での応用[編集]
地図学[編集]

地図学では、球面である地球を平面の地図に投影する図法の一つとして、ステレオ投影のことを平射図法(平射方位図法)またはステレオ図法と言う。角度(形)と面積を保ったまま球を平面に投影する地図は無い、という事実が地図学の基本的問題である。一般的に、統計学は積分をする傾向があるために、正積投影は統計向きである。一方、正角投影は航海目的に好ましい。平射図法は正角投影に分類される。また、地球のどちらかの極を中心に投影したとき、経線は原点から放射状にのび、緯線は原点を中心とする円になるという、方位図法としての特性が得られる。すなわち平射図法は正角方位図法である。
地球を赤道半径 、離心率 の回転楕円体とするとき、緯度 、経度 の点をXY平面に投影する式は以下のとおりである[10]。すなわち、座標原点を極点にとり、極点から赤道へ向かう方向を正方向とした中央経線をX軸に設定し、当該中央経線の経度を とするとき、
に投影する。ただし、 は、緯度 に対する等長緯度である。
以前は正角性に注目して使用されることも多かったが、近年ではメルカトル図法、横メルカトル図法(ガウス・クリューゲル図法)、斜軸メルカトル図法、ランベルト正角円錐図法などにほとんど置き換わり、ごく狭い国(オランダなど)や北極・南極などに限られるようになった。ただし天気図については、気圧や気温の傾斜を正角で観察する必要がある上に、北半球や南半球全体で考察することが増えたため、平射図法の使用が増えている。また「全ての小円が必ず円になる」という性質に着目して、クレーターが多い月面の全図に使われた例[11] がある。
結晶学[編集]

結晶学では、3次元空間内の結晶軸や結晶面の方向は、例えばX線や電子線回折パターンの解釈で中心となる幾何学的な概念である。 これらの方向は、上記の線と面の可視化の節で述べたように、可視化することができる。 それは、結晶軸と結晶面に対する極は、北半球に交わり、それゆえにステレオ投影を用いてプロットできる。 極点のプロットは、極点図形と呼ばれる。
地学[編集]
この節の加筆が望まれています。 |
写真[編集]

脚注[編集]
- ^ 訳注:本文中にもあるように、planisphereは「星図」の古い呼び名なので、星図投影とも読める。
- ^ a b Snyder (1993).
- ^ According to (Snyder 1993), although he acknowledges he did not personally see it
- ^ Snyder (1989).
- ^ According to (Elkins, 1988) who references Eckert, "Die Kartenwissenschaft", Berlin 1921, pp 121--123
- ^ Wulff, George, Untersuchungen im Gebiete der optischen Eigenschaften isomorpher Kristalle: Zeits. Krist.,36, l-28 (1902)
- ^ Cf. Apostol (1974) p. 17.
- ^ Cf. Pedoe (1988).
- ^ Cf. Shafarevich (1995).
- ^ 河瀬和重 (2014): Lambert正角円錐図法及びその極限としての平射図法の座標換算式に係る包括的導出に関する研究, 平成25年度調査研究年報, 国土地理院技術資料A4-No.12, 80–83
- ^ 月の地形図 国土地理院サイト
参考文献[編集]
- Apostol, Tom (1974). Mathematical Analysis (2 ed.). Addison-Wesley
- Brown, James and Churchill, Ruel (1989). Complex variables and applications. New York: McGraw-Hill. ISBN 0070109052
- German, Daniel; Burchill, L.; Duret-Lutz, A.; Pérez-Duarte, S.; Pérez-Duarte, E.; Sommers, J. (June 2007). "Flattening the Viewable Sphere". "Proceedings of Computational Aesthetics 2007". Banff: Eurographics. pp. 23--28.
- Do Carmo, Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7
- Elkins, James (1988). “Did Leonardo Develop a Theory of Curvilinear Perspective?: Together with Some Remarks on the 'Angle' and 'Distance' Axioms”. Journal of the Warburg and Courtauld Institutes 51: 190--196. doi:10.2307/751275.
- Oprea, John (2003). Differential geometry and applications. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0130652466
- Pedoe, Dan (1988). Geometry. Dover. ISBN 0-486-65812-0
- Shafarevich, Igor (1995). Basic Algebraic Geometry I. Springer. ISBN 0387548122
- Snyder, John P. (1989). An Album of Map Projections, Professional Paper 1453. US Geological Survey
- Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9
- Spivak, Michael (1999). A comprehensive introduction to differential geometry, Volume IV. Houston, Texas: Publish or Perish. ISBN 091409873X
関連項目[編集]
外部リンク[編集]
- Weisstein, Eric W. "Stereographic Projection". mathworld.wolfram.com (英語).
- stereographic projection in nLab
- stereographic projection - PlanetMath.(英語)
- Definition:Stereographic Projection at ProofWiki
- Bushmanova, G.V. (2001), “Stereographic projection”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
























