出典: フリー百科事典『ウィキペディア(Wikipedia)』
三角分布
確率密度関数  |
累積分布関数 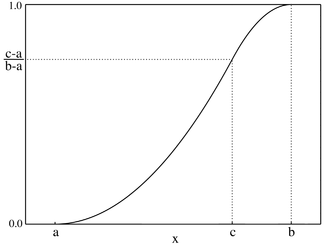 |
| 母数 |


![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249) |
|---|
| 台 |
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) |
|---|
| 確率密度関数 |
![{\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{for }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e4e98ad8069ea39f61fe2f0be5b83b47f631bc) |
|---|
| 累積分布関数 |
![{\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b472d4e58e4df0814805aab0a2e752d6bdebf3) |
|---|
| 期待値 |
 |
|---|
| 中央値 |
![{\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fe21e5d8eb394b9e5dca33a2c790c001328393) |
|---|
| 最頻値 |
 |
|---|
| 分散 |
 |
|---|
| 歪度 |
 |
|---|
| 尖度 |
 |
|---|
| エントロピー |
 |
|---|
| モーメント母関数 |
 |
|---|
| 特性関数 |
 |
|---|
| テンプレートを表示 |
確率論および統計学において、三角分布(さんかくぶんぷ、英: triangular distribution)とは、区間 [a, b] において次の確率密度関数を持った連続確率分布である。

ここで、パラメータ a は最小値、b は最大値、c は最頻値である。
三角分布の分布関数は

三角分布の平均 E(X) および分散 V(X) は、


|
|---|
離散単変量で
有限台 | |
|---|
離散単変量で
無限台 | |
|---|
連続単変量で
有界区間に台を持つ | |
|---|
連続単変量で
半無限区間に台を持つ | |
|---|
連続単変量で
実数直線全体に台を持つ | |
|---|
連続単変量で
タイプの変わる台を持つ | |
|---|
| 混連続-離散単変量 | |
|---|
| 多変量 (結合) | |
|---|
| 方向 | |
|---|
| 退化と特異 | |
|---|
| 族 | |
|---|
| サンプリング法(英語版) | |
|---|
|
|


![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{for }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e4e98ad8069ea39f61fe2f0be5b83b47f631bc)
![{\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b472d4e58e4df0814805aab0a2e752d6bdebf3)

![{\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fe21e5d8eb394b9e5dca33a2c790c001328393)










