等脚台形
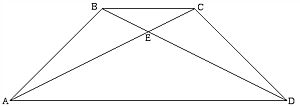
等脚台形(とうきゃくだいけい、米語:isosceles trapezoid, 英語:isosceles trapezium)は、台形の一種で、1本の底辺の両端の内角が互いに等しい図形である。このとき、もう一組の底辺の両端の内角も互いに等しくなる。等脚台形は線対称な図形であり、その対称軸は2本の底辺それぞれの中点をともに通る直線である。
等脚台形では右図での辺ABと辺CDのように台形の脚の長さが互いに等しくなる。等脚台形の名称はこの性質に由来するが、一方、平行四辺形も台形の一種であり、この場合、台形の脚の長さも等しくなるので、(等脚台形の脚の長さは等しいが)「脚の長さが等しい台形は、等脚台形である」という認識は誤りだと言える。
等脚台形のうち、底辺BCとADの長さも等しい場合は長方形となる。したがって長方形は等脚台形の特殊な形である。長方形とは、等脚台形であり、かつ平行四辺形でもある四角形だということができる。
等脚台形の面積Sを求める公式は台形の場合と同一で
と表される。ただし h は台形の高さで、この場合 BC と AD の距離にあたる。 4本の辺の長さ x, y, z, w=y が分かっている場合は以下の式で面積を求めることもできる。
ただし x と z は平行とする。
2本の対角線の長さは互いに等しく、対角線の交点Eと上底にある頂点B,Cまでの距離はともに等しい。下底にある頂点A,Dに対しても同様である。 また、三角形EABと三角形EDCは合同な図形となり、対角線の交点Eから台形の脚AB,CDまでの距離は等しい。
等脚台形は円に内接する。つまり4本の辺それぞれの垂直二等分線は一点で交わる。
正六角形を最も長い対角線を境に2つに分割すると4本の辺のうち3本の長さが等しい等脚台形が得られる。


