出典: フリー百科事典『ウィキペディア(Wikipedia)』
確率論および統計学において、ガンベル分布(ガンベルぶんぷ、英: Gumbel distribution)は、連続確率分布の一種である。さまざまな分布に従う確率変数の最大値(または最小値)が漸近的に従う分布であり、極値分布のタイプI型に相当する。分布の名は極値統計学の先駆的な研究を行ったドイツの数学者エミール・ユリウス・ガンベルに因む。
ガンベル分布を用いることで、ある河川の水位の年間の最大値のデータが過去10年分あれば、来年の最大水位を確率分布のかたちで予想することができる。
また稀にしか発生しない地震や洪水などの自然災害の発生する確率を予測することができる。
サンプルデータの分布が正規型または指数型である場合に、ガンベル分布は極値理論はこれらの予測に有用である。
ガンベル分布は最大値の分布をモデル化するが、最小値をモデル化するには元の値の負の値を使用するとよい。
ガンベル分布は、一般化極値分布(フィッシャー・ティペット分布とも呼ばれる)の特殊なケースである。
一般化極値分布は他には、対数ワイブル分布や二重指数分布(ラプラス分布)などがある。
確率密度分布を原点で反転させ、次に正の半直線に制限すると、ゴンペルツ分布が得られる。
多項ロジットモデル(離散選択理論では一般的)の潜在変数の定式化では、潜在変数の誤差はガンベル分布に従い、ガンベル分布を持つ2つの確率変数の差はロジスティック分布になる。
定数 μ と正の定数 η > 0 に対し、確率変数 X の分布関数 F(X) が
![{\displaystyle F(x)=\exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right],\quad -\infty <x<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7166974985c78b4b4b3a3ddd32f3c47926f11c63)
で与えられるとき、確率変数 X はガンベル分布に従うという。このとき、対応する確率密度関数 f (x) は
![{\displaystyle f(x)={\frac {1}{\eta }}\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right],\quad -\infty <x<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdd293638ce597245b6ae3177e1f1fabb2ac38d3)
である。ガンベル分布は極値分布のタイプIに相当する。
標準ガンベル分布[編集]
 かつ η =1のとき
かつ η =1のとき

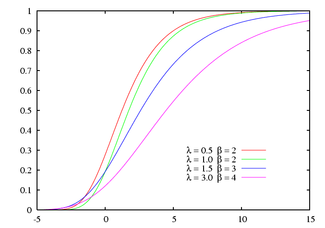
グラフの形状[編集]
・モード(最頻値) :
・メジアン(中央値): 
平均・分散[編集]
ガンベル分布の確率変数を X とするとき、平均 E(X) および分散 V(X) は次のように表される。


ここで γ = 0.577… はオイラーの定数である。
モーメント母関数・特性関数[編集]
ガンベル分布の確率変数を X とするとき、モーメント母関数 MX(t) は

で与えられる。ここで Γ(x) はガンマ関数を表す。
また、特性関数 φX(t) は

で与えられる。
キュムラント母関数・キュムラント[編集]
ガンベル分布の確率変数を X とするとき、キュムラント母関数 KX(t) は

で与えられる。
このとき、n 次のキュムラント κn は

となる。ここで ζ(n) はゼータ関数である。
参考文献[編集]
- Gumbel. E. J.:Statistics of Extremes, Columbia University Press, 1963.
関連項目[編集]
|
|---|
離散単変量で
有限台 | |
|---|
離散単変量で
無限台 | |
|---|
連続単変量で
有界区間に台を持つ | |
|---|
連続単変量で
半無限区間に台を持つ | |
|---|
連続単変量で
実数直線全体に台を持つ | |
|---|
連続単変量で
タイプの変わる台を持つ | |
|---|
| 混連続-離散単変量 | |
|---|
| 多変量 (結合) | |
|---|
| 方向 | |
|---|
| 退化と特異 | |
|---|
| 族 | |
|---|
| サンプリング法(英語版) | |
|---|
|
|






![{\displaystyle \times \exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d29fe59e87d9c4b8459338503c9591ff025365)
![{\displaystyle \exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f02db009d9882a34e15ec5e91168a5c3f163a83c)









![{\displaystyle F(x)=\exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right],\quad -\infty <x<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7166974985c78b4b4b3a3ddd32f3c47926f11c63)
![{\displaystyle f(x)={\frac {1}{\eta }}\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\exp \left[-\exp \left\{-\left({\frac {x-\mu }{\eta }}\right)\right\}\right],\quad -\infty <x<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdd293638ce597245b6ae3177e1f1fabb2ac38d3)








