ベンフォードの法則

ベンフォードの法則(ベンフォードのほうそく、Benford's law)とは、自然界に出てくる多くの(全てのではない)数値の最初の桁の分布が、一様ではなく、ある特定の分布になっている、という法則である。この法則によれば、最初の桁が1である確率はほぼ3分の1にも達し、大きな数値ほど最初の桁に現れる確率は小さくなり、9になると最初の桁に現れる確率は20分の1よりも小さくなる。数理的には、数値が対数的に分布しているときは常に最初の桁の数値がこのような分布で出現する。以下に示したような理由により、自然界での測定結果はしばしば対数的に分布する。別の言い方でいえば、対数的な測定結果があらゆる場所に存在する。
この直感に反するような結果は、電気料金の請求書、住所の番地、株価、人口の数値、死亡率、川の長さ、物理・数学定数、冪乗則で表現されるような過程(自然界ではとても一般的なものである)など、様々な種類の数値の集合に適用できることがわかっている。この法則はその数値の基底によらず(十進法ではない場合でも)適用できるが、その場合1桁目の各数値の取る比率は変化する。
1938年にこの法則を提唱した物理学者、フランク・ベンフォード (Frank Benford) にちなんで名づけられている[1]。しかしながら、この法則はそれ以前、1881年にサイモン・ニューカムによって提示されていた[2]。
また、このような数ないし自然の性質を人工的工学的に反映させたものに「標準数」がある。
数学的な表現[編集]
より形式的に記述すると、
- 基底が b (b ≥ 2) のときの最初の桁の数値 d (d ∈ {1, …, b − 1}) の出現確率は、P(d) = logb (d + 1) − logb d = logb ((d + 1)/d) という式に従う
となる。この数値は厳密に対数スケールにおいて d と d + 1 の間の空間に等しい。
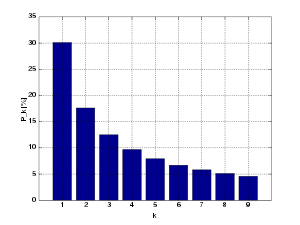
基底が10の場合(十進数)、ベンフォードの法則に従えば最初の桁の分布は以下のようになる。ただし d が最初の桁で p が確率である。
| d | p |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
説明[編集]
ベンフォードの法則は様々な観点から説明されてきた。
対数スケールにおける分布幅[編集]
 |
 |
上に示した2つの図は、対数スケールの上にプロットした2つの確率分布である[注 1]。どちらの図でも、赤で示した部分の面積が最初の桁が1である確率に比例しており、青で示した部分の面積が最初の桁が8である確率に比例している。
左側の分布では、赤と青の領域の面積比はおおよそそれぞれの幅の比に等しくなっている。幅の比は普遍的で、ベンフォードの法則によって厳密に与えられる。したがって、こうした確率分布に従う数値はおおむねベンフォードの法則に従う。
一方、右の分布では、赤と青の領域の面積比はその幅の比から大きく外れている。右の図でも幅の比は左側の分布と同じになっている。赤と青の領域の面積比は、その幅よりもむしろ高さの比に依存して決定されている。幅と異なり高さはベンフォードの法則に普遍的な関係を満たさない。代わりにその数値の分布の形によって完全に決定される。したがって、1桁目の数値の分布はベンフォードの法則を全く満たさない。
より一般的には、収入の分布や市町村の人口分布など、数桁の範囲でかなりスムーズに広がっているような分布は、上の左の図のようによくベンフォードの法則を満たす。一方、大人の身長やIQの数値など1桁か2桁の範囲でしか分布しないようなものは、上の右の図のようにベンフォードの法則をあまりよく満たさない[3]。
指数的な成長過程の結果[編集]
数値の対数が普遍的に分布していると考えれば、ベンフォードの法則の正確な形は説明できる。これは、たとえば100から1,000まで(対数で2から3まで)の間で分布しているのと、10,000から100,000まで(対数で4から5まで)の間で分布しているのとが同じようであるという意味である。多くの数の集合、特に収入や株価など指数的に大きくなる数値に関しては、これは合理的な仮定である。
単純な例で、どのようにこれが働くのかを説明する。ある量が「指数的に増加する」とは、別な言葉で言えば、その量が2倍になる時間は一定であるということである。その量が2倍になるのに1年掛かるのであれば、そのさらに1年後にはさらに2倍になる。2年後の終わりには元の値の4倍になり、3年後の終わりには元の値の8倍になる。ここでは、1年ごとに2倍になる値が、ちょうど100になった年から考えるものとする。この値の最初の桁は、最初の1年間はずっと1である。2年目には7ヶ月強の間2になり、残りの5ヶ月ほどの間3になる。3年目には4、5、6、7と次第に短い時間になっていく。4年目の初期には最初の桁は8と9になり、そしてこの量は1,000になる。そしてこの過程が再び最初から始まる。この例で、期間中任意の時期にこの量を測れば、最初の桁が1である時に測定する確率が高く、1桁目がより大きな値になるにつれて測定する確率はどんどん小さくなるということは簡単にわかる。
この例では、指数的に増大する値の測定結果がベンフォードの法則に従うであろうということを示した。しかし、指数的な増大が明白でない多くの場合にも法則が適用できるようにみえる。
スケール不変[編集]
この法則は代わりに以下のような事実からも説明することができる。もし本当に最初の桁の数値が特定の分布をしているのであれば、測定の単位を変更したとしても同様に特定の分布を示すはずである。たとえば、長さの測定値をフィートからヤードへ定数を掛けて変更したとしても、分布は不変でなければならない。これはスケール不変 (普遍) ということであり、こうした条件を満たす唯一の分布が対数的に分布しているものである。
例えば、何かの物体の長さや距離などの最初の桁(0は除く)は、測定単位がフィートやヤードやその他の何であれ、同じ分布でなければならない。1 ヤードは3 フィートであるので、ヤードで測定した長さの最初の桁が1である確率は、フィートで測定した長さの最初の桁が3、4、5のいずれかである確率と同じでなければならない。これをあらゆる測定単位に対して同じように考えると対数的な分布となり、log10(1) = 0 とlog10(10) = 1 であることを考え合わせると、ベンフォードの法則が得られる。つまり、最初の桁に特定の分布があるならば、それはどのような測定単位が用いられようとも適用できなければならず、そのような条件に適合する唯一の最初の桁の分布がベンフォードの法則であることになる。
多重確率分布[編集]

IQのスコア、人間の身長、その他正規分布に従う値の分布から得られた数値に対しては、この法則が有効ではないことは注意しなければならない。しかしながら、こうした分布から取った値を混合する、例えば新聞記事から数値を取ってくるなどすれば、再びベンフォードの法則が現れる。これは数学的に証明することができる。もし、確率分布を繰り返しランダムに選び、その選んだ分布からランダムに数値を選べば、得られる数値の集合はベンフォードの法則に従う[4][5]。
適用と制限[編集]
1972年、ハル・バリアン (Hal Varian) は、公共計画の決定を支援するために提出された社会経済学的なデータの一覧に含まれる作為的な値を発見するためにこの法則を利用できると示唆した。データを作為的に作成する人は、その数値をかなり普遍的に分布させるようにするであろうというもっともらしい仮定に基づけば、そのデータの最初の桁の分布確率をベンフォードの法則に従った場合の期待される分布確率と単純に比較することで、異常な結果が示されるはずである[6]。この考えに基づき、マーク・ニグリニ (Mark Nigrini) が、ベンフォードの法則が会計や支出に関する詐欺の指標として利用できることを示した[7]。
制限[編集]
しかしながら、こうした用法には注意を払う必要がある。実社会のデータは、そのデータの種類に応じて数値の分布の仕方が歪められていることがあり、その程度に応じてベンフォードの法則を満たさないことがある。
例えば、「名前が'A'で始まるイギリスの村の人口」とか「小額の保険金請求」とかがベンフォードの法則に従うと期待するかもしれない。しかし、イギリスでの村の定義が「人口が300人から999人までの集落」であることや、小額の保険金請求の定義が「50ドルから100ドルまでの請求」であることがわかれば、特定の値が定義によって排除されていることからベンフォードの法則を(単純には)適用できないことがわかる。
極端な例[編集]
二進表現では、この現象の最も極端な例があらわれる。通常の表記方法すなわち、いわゆる「先行する0」を取り除くと、二進表現では常に最上位桁は1である(「0」以外は)。この特性を巧妙に利用し最上位桁を省略する表現技法があり、「ケチ表現」と呼ばれている。
歴史[編集]
この法則の発見は1881年まで遡る。アメリカ人の天文学者であるサイモン・ニューカムが、その当時計算をするために用いられていた対数表で、1で始まる数値を記載している最初の方のページが、他のページに比べてずっと擦り切れていることに気付いた[2]。ニューカムが出版した結果は法則に関して知られている最初の例であり、また同様に2番目の桁の分布に関しても含んでいた。ニューカムは、最初の桁の数値を N とすると、その出現確率は log(N+1) − log(N) であるとする法則を提案した。
この法則は物理学者のフランク・ベンフォードによって1938年に再発見された[1]。彼は広い範囲のデータに対してこの法則を検証し、法則の名前も彼の名前から取られた。1996年にテッド・ヒル (Ted Hill) が前述した複数の分布からの数値を混合した分布についての法則を証明した[5]。
最初の桁以降への一般化[編集]
この法則を最初の桁以降についても拡張することができる[8]。特に、一連の数値nで始まる数に遭遇する確率は、
で与えられる。例えば、数字の最初の3桁が"314"で始まる確率は log10(1 + 1⁄314) である。この結果を用いて、数値中のある特定の桁にある数値が現れる確率を求めることができる。例えば、最初から2桁目に"2"が出てくる確率は[8]
となる。n 番目の桁の数値分布は、n が増加するにつれて急速にどの数値に対しても一様分布である10%へと近づいていく[8]。
実際に、ベンフォードの法則の不正発見目的における利用では、普通は2桁目以降も用いる[7]。
関連項目[編集]
脚注[編集]
注釈[編集]
- ^ もし線形スケールの通常の確率分布で考えるならば、対数スケールでの適切な確率分布を求めるためにはある関数を掛ける必要がある。対数スケールは水平方向の距離を歪めるので、カーブの各区間の下部の面積が元の分布に一致するようにするために高さ方向も変える必要がある。
出典[編集]
- ^ a b Frank Benford (March 1938). “The law of anomalous numbers”. Proceedings of the American Philosophical Society 78 (4): 551–572.(入会が必要)
- ^ a b Simon Newcomb (1881). “Note on the frequency of use of the different digits in natural numbers”. American Journal of Mathematics 4 (1/4): 39–40. doi:10.2307/2369148.(入会が必要)
- ^ R. M. Fewster, "A simple explanation of Benford's Law", The American Statistician. February 1, 2009, 63(1): 26-32. 直接リンク
- ^ Theodore P. Hill (July–August 1998). “The first digit phenomenon” (PDF). American Scientist 86: 358.
- ^ a b Theodore P. Hill (1996). “A statistical derivation of the significant-digit law” (PDF). Statistical Science 10: 354–363.
- ^ Varian, Hal, “Benford's law”, The American Statistician 26: 65
- ^ a b Mark J. Nigrini (May 1999). “I've Got Your Number”. Journal of Accountancy.
- ^ a b c Theodore P. Hill, "The Significant-Digit Phenomenon", The American Mathematical Monthly, Vol. 102, No. 4, (Apr., 1995), pp. 322-327. Official web link(入会が必要). 代替の無料のウェブリンク.
関連文献[編集]
- Sehity et al. (2005). “Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction”. International Journal of Research in Marketing 22: 471–480. doi:10.1016/j.ijresmar.2005.09.002.
- Wendy Cho and Brian Gaines (August 2007). “Breaking the (Benford) Law: statistical fraud detection in campaign finance.”. The American Statistician 61 (3): 218–223. doi:10.1198/000313007X223496.
- L.V.Furlan (June 1948). “Die Harmoniegesetz der Statistik: Eune Untersuchung uber die metrische Interdependenz der soziale Erscheinungen”. Reviewed in Journal of the American Statistical Association 43 (242): 325–328.
- Mark J. Nigrini: "Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection", Wiley, ISBN 978-1118152850 (2012年4月).
- Steven J. Miller (Eds): "Benford's Law: Theory and Applications", Princeton University Press, ISBN 978-0691147611 (2015年5月).
外部リンク[編集]
- Benford's Law and Zipf's Law (英語)
- Following Benford's Law, or Looking Out for No. 1 (英語)
- I've Got Your Number - マーク・ニグリニによる (英語)
- Video showing Benford's Law applied to Web Data (incl. Minnesota Lakes, US Census Data and Digg Statistics) (英語)
- A further five numbers: number 1 and Benford's law - サイモン・シンによる (英語)
- Looking out for number one - ジョン・ワルソー、ロバート・ハント、マーク・ピアソン、plus Magazine, September 1999 (英語)
- Weisstein, Eric W. "Benford's Law". mathworld.wolfram.com (英語).
- Benford's Law - MathPages上のサイト (英語)
- Benford's Law from Ratios of Random Numbers - ウルフラム・デモンストレーション・プロジェクトのフィオナ・マクラクランによる (英語)
- Ted Hill's personal website 特に CV に彼のベンフォードの法則に関する文献の一覧がある、ほとんどに無料のリンクがつけられている (英語)
- Entropy Principle in Direct Derivation of Benford's Law オーディッド・カフリによる、arXiv上のページ (英語)
- New Pattern Found in Prime Numbers (英語)
- A demonstration of the Generalized Benford's Law on Prime Numbers (英語)
- ベンフォードの法則…数字の不思議な法則


