クーポンコレクター問題
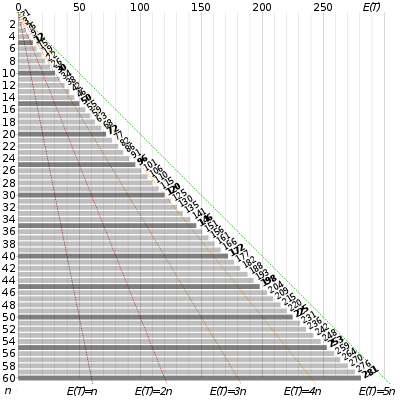
確率論において、クーポンコレクター問題(クーポンコレクターもんだい、英語: Coupon collector's problem)とは、 「全てのクーポンを集めると、何らかの特典が得られる」ような場合に、何回クーポンを引けば良いかという問題である。「クーポンコレクター」と表現しているが、ソーシャルゲームにおけるコンプリートガチャや、(全て集めることで特典があるわけではないが)カプセルトイ・食玩・トレーディングカード等で全種類を集める場合にも適用できる問題である。日本においては食玩問題 [1]とも呼ばれる。
具体的には次のような問題である。
- 壺の中に n 種類の異なるクーポンが入っている。1回の試行で壺の中から1枚クーポンを引き、引いたものと同じ種類のクーポンを壺の中に戻すものとする。n 種類(全種類)のクーポンを集めようとしたとき、 t 回以上の試行回数が必要となる確率はいくつだろうか?
別の言い方をすると次のようになる。
- n 種類の異なるクーポンがあるとき、各種類のクーポンを1回以上引くまでに、何回クーポンを引けば良いか?
数学的分析によれば、必要とされる試行回数の期待値は である[注釈 1]。例えば n = 50の場合、全50種類のクーポンを収集するには、平均で約225回の試行が必要となる[注釈 2]。
解法[編集]
期待値の計算[編集]
T を全 n 種のクーポンを収集する時間とし、 ti を i - 1種のクーポンを収集した後に i 種類目のクーポンを収集する時間とする。T と ti を確率変数と考える。新しいクーポンを集める確率は pi = (n − (i − 1))/n である。従って、 ti は期待値を1/pi とする幾何分布となる。期待値の線形性により、以下が得られる。
ここで、 Hn は n 番目の調和数である。 調和数の漸近解析を使用して、以下が得られる。
ここで、 はオイラーの定数である。
マルコフの不等式を使用して、所望の確率の上限を与えることができる。
分散の計算[編集]
確率変数 ti の独立性を用いて、分散が以下のように計算できる。
なぜならば、 であるからである(バーゼル問題を参照)。
チェビシェフの不等式を使用して、所望の確率を決めることができる。
テールの推定[編集]
異なる上限は、以下の計算から導き出すことができる。 を最初の 回の試行で 番目のクーポンが引けない事象を表すとする。
したがって、についてはとなる。
拡張と一般化[編集]
- ポール・エルデシュとレーニ・アルフレードは、 T の分布の極限定理を証明した。この結果は、ここまでに述べた境界のさらなる拡張である。
- ドナルド・J・ニューマンとローレンス・シェップは、全クーポンを m 枚ずつ収集する必要がある場合として、クーポンコレクター問題を一般化した。各クーポンを m 枚収集するのにかかる時間を Tm とする。彼らは、この場合の期待値が以下を満たしていることを示した。
- ここで、 m は固定されている。 m = 1のとき、上述の式が得られる。
- 同じ一般化のもとでエルデシュとレーニは以下を導いた。
- フィリップ・フラジョレ[2]によると、不均一な確率分布の一般的なケースでは、以下のようになる。
関連項目[編集]
脚注[編集]
注釈[編集]
出典[編集]
- ^ “食玩問題”. 2017年9月11日閲覧。
- ^ Flajolet, Philippe; Gardy, Danièle; Thimonier, Loÿs (1992), “Birthday paradox, coupon collectors, caching algorithms and self-organizing search”, Discrete Applied Mathematics 39 (3): 207–229, doi:10.1016/0166-218x(92)90177-c
出典[編集]
- Blom, Gunnar; Holst, Lars; Sandell, Dennis (1994), “7.5 Coupon collecting I, 7.6 Coupon collecting II, and 15.4 Coupon collecting III”, Problems and Snapshots from the World of Probability, New York: Springer-Verlag, pp. 85–87, 191, ISBN 0-387-94161-4, MR1265713.
- Dawkins, Brian (1991), “Siobhan's problem: the coupon collector revisited”, The American Statistician 45 (1): 76–82, doi:10.2307/2685247, JSTOR 2685247.
- Erdős, Paul; Rényi, Alfréd (1961), “On a classical problem of probability theory”, Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 6: 215–220, MR0150807.
- Newman, Donald J.; Shepp, Lawrence (1960), “The double dixie cup problem”, American Mathematical Monthly 67: 58–61, doi:10.2307/2308930, MR0120672
- Flajolet, Philippe; Gardy, Danièle; Thimonier, Loÿs (1992), “Birthday paradox, coupon collectors, caching algorithms and self-organizing search”, Discrete Applied Mathematics 39 (3): 207–229, doi:10.1016/0166-218X(92)90177-C, MR1189469.
- Isaac, Richard (1995), “8.4 The coupon collector's problem solved”, The Pleasures of Probability, Undergraduate Texts in Mathematics, New York: Springer-Verlag, pp. 80–82, ISBN 0-387-94415-X, MR1329545.
- Motwani, Rajeev; Raghavan, Prabhakar (1995), “3.6. The Coupon Collector's Problem”, Randomized algorithms, Cambridge: Cambridge University Press, pp. 57–63, MR1344451.
外部リンク[編集]
- "Coupon Collector Problem" by Ed Pegg, Jr., the Wolfram Demonstrations Project. Mathematica package.
- How Many Singles, Doubles, Triples, Etc., Should The Coupon Collector Expect?, a short note by Doron Zeilberger.












![{\displaystyle {\begin{aligned}P\left[{Z}_{i}^{r}\right]=\left(1-{\frac {1}{n}}\right)^{r}\leq e^{-r/n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67a53982df76dc7d07840b856926f1e1c66f71d8)

![{\displaystyle P\left[{Z}_{i}^{r}\right]\leq e^{(-\beta n\log n)/n}=n^{-\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/916bd3a3939a0a68c3c412c893da118eb58826c5)
![{\displaystyle {\begin{aligned}P\left[T>\beta n\log n\right]=P\left[\bigcup _{i}{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n\log n}]\leq n^{-\beta +1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0619da74b895fd016b2edf04cc11e5bac2aa8004)





