凸集合
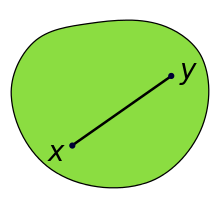

ユークリッド空間における物体が凸(とつ、英: convex)であるとは、その物体に含まれる任意の二点に対し、それら二点を結ぶ線分上の任意の点がまたその物体に含まれることを言う。例えば中身のつまった立方体は凸であるが、例えば三日月形のように窪みや凹みのあるものは何れも凸でない。凸曲線は凸集合の境界を成す。
凸集合の概念は後で述べるとおり他の空間へも一般化することができる。
ベクトル空間内の凸集合[編集]
S は実数体(あるいはより一般に適当な順序体)上のベクトル空間とする。ユークリッド空間はその例である。S 内の集合 C が凸であるとは、任意の x, y ∈ C および任意の t ∈ [0, 1] に対し、点 (1 − t)x + ty もまた C に属することをいう。即ち、x と y とを結ぶ線分上の各点が C に属する[1]。これにより、実または複素位相線型空間における凸集合は弧状連結、したがって連結であることが従う。 さらに、C が狭義凸 (strictly convex) であるとは、x と y とを結ぶ線分上の各点が端点を除き C の内部に含まれるときにいう。
実数全体の成す集合 R の凸部分集合とは、単に R の区間のことである。ユークリッド平面の凸部分集合の例には、中身のつまった正多角形、中身のつまった三角形、中身のつまった三角形の交わり、などが挙げられる。三次元ユークリッド空間の凸部分集合の例にはアルキメデスの立体、プラトンの立体などが挙げられる。ケプラー・ポアンソ多面体は非凸集合の例である。
凹集合[編集]
凸でない集合は非凸集合 (non-convex set) と言う。凸多角形でない多角形は凹多角形とも呼ばれ[2]:130、文献によってはより一般に非凸集合をあらわすのに凹集合 (concave set) という語を使用することもある[3]が、普通はそのような言い方は避けられる[注釈 1][注釈 2]。
性質[編集]
S が n-次元空間内の凸集合ならば、任意 r-個 (r > 1) の n-次元ベクトル u1, …, ur ∈ S と任意の非負数 λ1, …, λr で λ1 + ⋯ + λr = 1 を満たすものに対し
が成り立つ。このように書かれるベクトルは、u1, …, ur の凸結合と呼ばれる。
交叉と合併[編集]
最後の凸集合の合併に関する性質については、合併をとる対象を包含関係を持つ列に制限することが大切である(ふたつの凸集合の合併は必ずしも凸集合でない)。
閉凸集合[編集]
閉凸集合は、その極限点をすべて自身に含むような凸集合である。これらは、閉半空間(超平面の片側に位置する空間内の点の集合)たちの交わりとして特徴付けることができる。
今述べたことのうち、そのよう交わりに書けるものが凸であり、それらが閉集合であるということは明らかである。その逆(つまり、任意の凸集合がそのような交わりとして表されること)を言うには、「閉凸集合 C とその外点 P が与えられたとき、C を含み P を含まない閉半空間 H が存在する」という形の支持超平面定理が必要になる。この支持超平面定理は、函数解析学におけるハーン・バナッハの定理の特別な場合である。
凸包とミンコフスキー和[編集]
凸包[編集]
ベクトル空間の部分集合 A は、もっとも小さな凸集合(A の凸包と呼ぶ)に含まれる。すなわち、凸包は、A を含むすべての凸集合の交叉である。凸包作用素 Conv() は包作用素を特徴づける性質をもつ。
凸包作用素は、凸集合全体の成す集合族が束を形成するために必要であり、その中で結び演算 ∨ は、2つの凸集合の合併の凸包
- Conv(S) ∨ Conv(T) ≔ Conv(S ∪ T) = Conv(Conv(S) ∪ Conv(T))
として定義される。凸集合の任意の交叉は凸集合であり、従って(実または複素)ベクトル空間の凸部分集合全体は完備束を成す。
ミンコフスキーの和[編集]

実線型空間において、二つの空でない集合 S1, S2 のミンコフスキー和 S1 + S2 は、加えられる各集合の元ごとの和の集合
として定義される。より一般に、空でない部分集合の有限族 Sn のミンコフスキー和は、同様に元ごとの和をとって
で与えられる。ミンコフスキー和に関して、零ベクトルのみからなる集合 {0} は特に重要である: 空でない任意の部分集合 S に対して
- S + {0} = S;
代数の言葉で言えば {0} は(空でない集合族上の)ミンコフスキー和の単位元である[注釈 3]。
ミンコフスキー和の凸包[編集]
ミンコフスキー和は、凸包を取る操作に関して以下の命題が示す通りよく振舞う。
S1, S2 を実ベクトル空間の部分集合とすると、それらのミンコフスキー和の凸包は、凸包のミンコフスキー和
- Conv(S1 + S2) = Conv(S1) + Conv(S2)
である。
この結果は、有限個の空でない集合の集まりに対して、より一般的に成り立つ。
数学的な言い方をすれば、ミンコフスキー和と凸包を作る操作は、可換な操作である[8](Theorem 3 (pp. 562–563))[注釈 4]
凸集合のミンコフスキー和[編集]
2つのコンパクトな凸集合のミンコフスキー和はコンパクトであり、コンパクト凸集合と閉凸集合の和は閉である[10]。
凸性の一般化と拡張[編集]
ユークリッド空間内の凸性の概念は、定義の一部を修正またはほかのものに取り換えて一般化することができる。「一般化された凸性」という語は、得られる対象が凸集合たちの持つある種の性質を保っていることを示唆して用いられる。
星状凸[編集]
C を実または複素ベクトル空間内の集合とする。C が星状凸であるとは、C の点 x0 が存在して、x0 から C の任意の点 y へ結ぶ線分が再び C に全く含まれる場合をいう。従って、空でない凸集合は必ず星状凸であるが、星状凸集合は必ずしも凸でない。
直交凸[編集]
一般化凸性の例として、直交凸性がある[11]。
ユークリッド空間内の集合 S が直交凸であるとは、S の二点を結ぶ任意の座標軸に平行な任意の線分全体が、S の中に含まれる場合を言う。直交凸性を持つ集合の交叉が直交凸であることを証明することは容易である。凸集合の持つ他の性質も成立する。
非ユークリッド幾何学[編集]
任意の二点を結ぶ(直線の代わりに)測地線を含む集合として測地的凸集合を定義することにより、凸集合や凸包の概念を非ユークリッド幾何学に対するものへ自然に拡張することができる。
順序位相[編集]
順序位相を持つ空間 X に対しても、その空間の全順序 < を用いて、凸性の概念を定義することができる[12][13]。
Y ⊆ X とするとき、部分空間 Y が凸集合であるとは、Y の任意の二点 a, b で a < b を満たすものに対して、区間 (a, b) = {x ∈ X : a < x < b} が Y に含まれるときにいう。つまり、Y が凸となる必要十分条件は、任意の a, b ∈ Y に対し、a < b ならば (a, b) ⊆ Y が成り立つことである。
凸型空間[編集]
凸性の持つ特定の性質を公理として、ほかの対象へ凸性を一般化することができる。
与えられた集合 X に対し、X 上の凸型 (convexity) とは X の部分集合族 𝒞 であって以下の公理系を満足するものを言う[14][6][7]:
- 空集合 ∅ および X は 𝒞 に属する。
- 𝒞 の元からなる任意の集合族の交わりは 𝒞 に属する。
- 𝒞 の元からなる(包含関係に関して)全順序な集合族の合併は 𝒞 に属する。
凸型 𝒞 の元を凸集合と呼び、対 (X, 𝒞) を凸型空間 (convexity space) と呼ぶ。通常の意味の凸性に対して、前二つの公理が成立する(三つ目は自明である)。
このように抽象的な凸性の、より離散幾何学に適した別定義は、反マトロイド(抽象的凸幾何)に関連する凸幾何学を参照せよ。
脚注[編集]
注釈[編集]
- ^ Takayama (1994)「しばしばみられる混乱が『凹集合』である。凹函数と凸函数はある種の函数のクラスを指すのであって集合のではない、その一方凸集合は集合のある種のクラスを指すのであって函数のではない。『凹集合』は集合か函数か紛らわしい」[4]:54
- ^ Corbae, Stinchcombe & Zeman (2009)「凹集合というようなものは存在しない」[5]:347
- ^ 空集合はミンコフスキー和において重要である。空集合は他の任意の部分集合を零化 (annihilate) する: 任意の部分集合 S に対して、それと空集合との和 S + ∅ = ∅ は空集合である。
- ^ ミンコフスキー和と凸化の可換性は (Schneider 1993, pp. 2–3, Theorem 1.1.2) を参照。(Schneider 1993, pp. 126–196, Chapter 3 Minkowski addition) はミンコフスキー和集合の凸包に関する多くの文献を論じている[9]
出典[編集]
- ^ 寒野善博 2019, pp. 81–82.
- ^ McConnell, Jeffrey J. (2006), Computer Graphics: Theory Into Practice, ISBN 0-7637-2250-2.
- ^ Weisstein, Eric W. "Concave". mathworld.wolfram.com (英語).
- ^ Takayama, Akira (1994), Analytical Methods in Economics, University of Michigan Press, ISBN 9780472081356
- ^ Corbae, Dean; Stinchcombe, Maxwell B.; Zeman, Juraj (2009), An Introduction to Mathematical Analysis for Economic Theory and Econometrics, Princeton University Press, ISBN 9781400833085
- ^ a b Soltan, Valeriu, Introduction to the Axiomatic Theory of Convexity, Ştiinţa, Chişinău, 1984 (in Russian).
- ^ a b Singer, Ivan (1997). Abstract convex analysis. Canadian Mathematical Society series of monographs and advanced texts. New York: John Wiley & Sons, Inc.. pp. xxii+491. ISBN 0-471-16015-6. MR1461544
- ^ Krein, M.; Šmulian, V. (1940年). “On regularly convex sets in the space conjugate to a Banach space”. Annals of Mathematics (2), Second series 41: pp. 556–583. doi:10.2307/1968735
- ^ Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. pp. xiv+490. ISBN 0-521-35220-7. MR1216521
- ^ Lemma 5.3: Aliprantis, C.D.; Border, K.C. (2006). Infinite Dimensional Analysis, A Hitchhiker's Guide. Berlin: Springer. ISBN 978-3-540-29587-7
- ^ Rawlins G.J.E. and Wood D, "Ortho-convexity and its generalizations", in: Computational Morphology, 137-152. Elsevier, 1988.
- ^ Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.
- ^ Definition:Convex Set (Order Theory) at ProofWiki
- ^ van De Vel, Marcel L. J. (1993). Theory of convex structures. North-Holland Mathematical Library. Amsterdam: North-Holland Publishing Co.. pp. xvi+540. ISBN 0-444-81505-8. MR1234493
参考文献[編集]
- 寒野善博、駒木文保『最適化手法入門』講談社、2019年。ISBN 9784065170083。
関連項目[編集]
外部リンク[編集]
- convex set in nLab
- Weisstein, Eric W. "Convex Set". mathworld.wolfram.com (英語).
- convex set - PlanetMath.(英語)
- Definition:Convex Set (Vector Space) at ProofWiki
- Burago, Yu.D.; Zalgaller, V.A. (2001), “Convex set”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4




