調和級数

数学における調和級数（ちょうわきゅうすう、英: harmonic series）とは発散無限級数

$\sum_{n=1}^\infty \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots$

のことをいう。名称の「調和」(harmonics) というのは音楽や和声学における倍音の概念に由来するもので、振動弦の倍音の波長というのが弦の基本波長の 1/2, 1/3, 1/4, ... となっていることによる。調和級数の各項は前後の項の調和平均になっており、また調和平均という用語もやはり音楽に由来するものである。

歴史

史実として、調和級数が発散することの最初の証明は14世紀のニコル・オレームによるものだが、これには誤りがあった。後に正しい証明がなされるのは17世紀、ピエトロ・モンゴリ、ヨハン・ベルヌーイ、ヤコブ・ベルヌーイらによってである。

歴史的には、調和数列は建築学の観点からの需要があった。特にバロック時代には、平面図や立面図での均衡をとるために、あるいは教会や宮殿の内装と外装の構造的詳細の調和関係を確立するために用いられた。

導入

調和級数は、その項の極限が 0 になるにもかかわらず発散するという意味で、初学者にとっては直観的ではない級数である。つまり、0 に収斂する数列の無限和が必ずしも有限でないかもしれないということが示される。調和級数が発散することに起因するいくつかの逆理や直観に反する結果が知られている。

例えば、「ゴムひもの上の芋虫」("worm on the rubber band") と呼ばれる逆理がある。内容は「芋虫が 1 メートルのゴムひもの上を這うものとし、そのひもは毎分 1 メートル伸びるものとする。芋虫は毎分 1 センチ進むとすると、芋虫はひもの端まで到達できるだろうか」といったものである。答えは、直観に反して「到達できる」である。実際、n 分後には、芋虫が進んだ合計距離がひもの長さに占める割合は

$\frac{1}{100}\sum_{k=1}^n\frac{1}{k}$

となっている。この級数は n を大きくすればいくらでも大きくすることができ、ついにはこの比が 1 を超えるようにすることができるが、それはつまり芋虫が端まで到達したという意味である。ただし、そのようなことになるためには n の値を極めて大きくする必要がある（凡そ e¹⁰⁰ 程度で、これは 1 のあとに 0 が 40 個つづくような数よりも大きい規模である）。調和級数は確かに発散するが、その発散は非常にゆっくりとしたものなのである。

別な例として「まったく同じドミノの集まりが与えられたとき、それをテーブルの縁に積み上げることができるのは明らかだが、それではテーブルのへりを（どの程度）張り出すように積めるか」というものが挙げられる。この直観的でない結果というのは、「ドミノが十分あれば、いくらでも好きなだけ張り出させることができる」である。

発散性

調和級数は正の無限大 +∞ に発散する。この事実を証明する方法はよく知られたものがいくつか存在する。

比較判定法

調和級数の発散性を示す方法の一つは別の発散級数と比較することである。調和級数の各項は、以下の第二の級数の対応する項よりも大きいかさもなくば一致するので、調和級数の和の値は第二の級数よりも大きい。

$\begin{align} & 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{3} + \frac{1}{4}\right) + \left(\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}\right) + \left(\frac{1}{9} +\right. \cdots \\[12pt] > {}& 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{4} + \frac{1}{4}\right) + \left(\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\right) + \left(\frac{1}{16} +\right. \cdots\\[12pt] = {}& 1 +\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots = \infty. \end{align}$

しかし、第二の級数の値は無限大であるから比較判定法により、調和級数の和も同様に無限大となる。もっとはっきり述べれば、上記の証明において比較

$\sum_{n=1}^{\,2^k\!}\frac{1}{n} > 1 + \frac{k}{2}$

が任意の正の整数 k に対して成立する。この証明はニコル・オレームによるもので、中世の数学の極みである。現在では、この方法が教科書的な証明の標準的なものとして教えられている。コーシーの判定法はこの方法を一般化したものになっている。

積分判定法

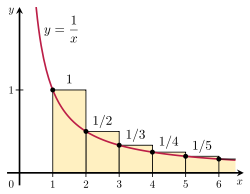
調和級数の発散をある広義積分との比較によって示すこともできる。これには調和級数の各項に対応する面積をもつ可算無限個の長方形の集まりを考える。各 n-番目の項に対応する長方形は、単位長さ 1 の幅と単位長さの 1/n の高さを持つものとすれば、これらの長方形の面積の合計は調和級数

$1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots$

の値に一致する。一方、曲線 y = 1/x の x が 1 から無限大までの部分の下にある面積は広義積分

$\int_1^\infty\frac{dx}{x} = \infty$

である。この面積は先ほどの長方形たちによって完全に覆われるから、長方形の面積の合計も同様に無限大となる。もっとはっきり述べれば、

$\sum_{n=1}^k \frac{1}{n} > \int_1^{k+1} \frac{dx}{x} = \ln(k+1)$

が示されたということになる。このような手法を一般に積分判定法という。

発散率

調和級数の発散は非常に遅く、たとえば最初の 10⁴³ 個の項の和は 100 よりも小さい。これは部分和が対数的増加であることによる。特に

$\sum_{n=1}^k\frac{1}{n} = \ln k + \gamma + \varepsilon_k$

が成り立つ。ここで γ はオイラー・マスケローニ定数で ε_k は k → ∞ の極限で 0 に近づく。この結果はオイラーによる。

部分和

発散する調和級数の第 n-部分和

$H_n = \sum_{k = 1}^n \frac{1}{k}$

は第 n-調和数 と呼ばれる。

n-番目の調和数と n の自然対数との差は、オイラーの定数に収斂する。相異なる番号の調和数同士の差は決して整数にはならない。また、n = 1 を除いてどの調和数も整数でない。

関連のある級数

交代調和級数

交代調和級数の最初の14個の部分和（黒線分）。2 の自然対数（赤線）に近づく様子が見られる。

級数

$\sum_{n = 1}^\infty \frac{(-1)^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots$

は交代調和級数 (alternating harmonic series) として知られる。この級数の収斂性はライプニッツの収斂判定法からわかる。とくにこの級数の和は 2 の自然対数に等しい。つまり

$1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots = \ln 2$

が成り立つ。この式は自然対数函数のテイラー級数であるメルカトール級数の特別な場合である。

逆正接函数のテイラー級数から、関連する級数

$\sum_{n = 0}^\infty \frac{(-1)^{n}}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots = \frac{\pi}{4}$

が導かれる。これはライプニッツの π の公式として知られる。

一般調和級数

一般調和級数 (general harmonic series) は a, b を実数で a ≠ 0 なるものとして

$\sum_{n=0}^{\infty}\frac{1}{an+b}$

という形に表される級数である。比較判定法により、任意の一般調和級数が発散することが示せる。

p-級数

調和級数の一般化で p-級数 (p-series) と呼ばれるものは、正の実数 p を用いて

$\sum_{n=1}^{\infty}\frac{1}{n^p}$

の形に表される。p = 1 のときの p-級数は通常の調和級数であり、発散する。積分判定法やコーシーの判定法を用いれば、p-級数は p > 1 なる全ての p について収斂する（このときの p-級数は、優調和級数 (over-harmonic series) とも呼ばれる）。また、p ≤ 1 なるすべての p について発散する。p > 1 ならば p-級数の和の値はリーマンゼータ函数の p における値 ζ(p) に等しい。

φ-級数

実数値凸函数 φ で

$\limsup_{u\to 0^{+}}\frac{\varphi(\frac{u}{2})}{\varphi(u)}< \frac{1}{2}$

を満たすものに対し、級数 ∑_n≥1 φ(n⁻¹) は必ず収斂する。

確率調和級数

アルバータ大学のバイロン・シュムランド (Byron Schmuland) は確率調和級数 (random harmonic series)

$\sum_{n=1}^{\infty}\frac{s_{n}}{n}$

の性質について研究した。分子の s_n は ±1 の値をそれぞれ 1/2 の等確率でとる独立同分布確率変数列である。シュムランドはこの和がほとんど確実に収斂し、その極限がいくつかの興味深い性質を持った確率変数となることを示した。特に、その確率変数の確率密度函数 ±2 における値は

0.124 999 999 999 999 999 999 999 999 999 999 999 999 999 764…

で、これは 1/8 よりも 10⁻⁴² ほど小さい。シュムランドの論文には、この確率が 1/8 に近いが一致するわけではないことの説明が示されている。

劣化調和級数

詳細は「ケンプナー級数」を参照

劣化調和級数 (depleted harmonic series) は、調和級数の項のうち、分母の十進表示の各位の数のどこかに 9 が現れるものを全て排除することで得られる級数である。劣化調和級数は収斂して、その値は 80 に満たないことが示せる。実は、十進表示列からどの特定の数字列を取り除いたとしても、そうして得られる級数は収斂する。

関連項目

• 複素対数函数
• ラグリアスの定理
• 調和数列

参考文献

• Weisstein, Eric W., "Harmonic Series" - MathWorld.（英語）
• "Harmonic Series" at Springer Encyclopaedia of Mathematics

外部リンク

• "The Harmonic Series Diverges Again and Again", The AMATYC Review, 27 (2006), pp. 31–43. Many proofs of divergence of harmonic series.