エッジワース・ボックス・ダイアグラム
| 経済学 |
|---|
 |
| 理論 |
| ミクロ経済学 マクロ経済学 数理経済学 |
| 実証 |
| 計量経済学 実験経済学 経済史 |
| 応用 |
|
公共 医療 環境 天然資源 農業 開発 国際 都市 空間 地域 地理 労働 教育 人口 人事 産業 法 文化 金融 行動 |
| 一覧 |
|
経済学者 学術雑誌 重要書籍 カテゴリ 索引 概要 |
| 経済 |
|
|
エッジワース・ボックス・ダイアグラム(英: The Edgeworth box diagram)とは、消費者理論において2財×2消費者の財空間を表現した図、あるいは生産者理論において2生産要素×2生産者の要素空間を表現した図のこと。フランシス・エッジワースに因んだ名称である[1][2]。アーサー・ボーリーの貢献も踏まえてエッジワース=ボーリー・ボックス・ダイアグラム(英:The Edgeworth-Bowley box diagram)とも呼ばれる[3]。
概要
[編集]
2財×2消費者の経済が図1に示されている。2財を財Xと財Yとする。横軸は財Xの数量Ωx、縦軸は財Yの数量Ωyである。2人の消費者をオクタビオ(Octavio)とアビー(Abby)とする。左下の原点はオクタビオの原点で、右上の原点はアビーの原点である。原点から遠ざかれば遠ざかるほどその消費者への配分が増える。つまり、右上の原点はオクタビオが全ての財Xと全ての財Yを保有する配分を示す。一方で、左下の原点はアビーが全ての財Xと全ての財Yを保有する配分を示す。
図中の青の線はオクタビオの無差別曲線で、オクタビオの原点(左下)を起点に描かれている。図中のオレンジの線はアビーの無差別曲線で、アビーの原点(右上)を起点に描かれている。配分点が右上に行けば行くほど、オクタビオの消費量が増え彼の効用水準が上昇するが、一方でアビーの消費量は減り、彼女の効用水準は低下する。
無差別曲線は通常凸(英:convex)であると仮定され、一方の財の消費量だけ増やしても限界効用が逓減することを意味している。市場経済における交換は、初期賦存量(英:endowment)から始まる。
エッジワース・ボックス・ダイアグラムは、一般均衡を視覚的に表現する目的で使用される。双方独占の状況では効率的な配分に行きつくことが難しいことも示すことができる[4]。一意の数値解が得られるゲーム理論における交渉問題においても用いられる[5][6]。
歴史
[編集]ダイアグラムの歴史
[編集]フランシス・エッジワースが、初めてエッジワース・ボックス・ダイアグラムの概念を提示した[1][2]。エッジワースが提示した2軸図は、ヴィルフレド・パレートの貢献によって現在の形に発展し[7]、アーサー・ボーリーの貢献で普及した。
均衡理論の歴史
[編集]市場均衡の概念はレオン・ワルラスによって提示され[8]、ヴィルフレド・パレートの貢献でさらに発展した[9]。エイブラハム・ウォールド、ポール・サミュエルソン、ケネス・アロー、ジェラール・ドブルーも数学的精緻化に貢献した[10][11][12]。選択公理に依存しない数理経済理論の構築、意思決定理論の数学的厳密化の流れの中でこのような貢献がなされた。
ワルラス的市場における均衡理論では、以下のような前提が必要である。
- 関数が微分可能である。
- 無差別曲線が効用関数から導出される。
- 無差別曲線が凸である。
さらに、非可逆性(英:Non-reversibility)や局所非飽和(英:Local nonsatiation)などの仮定を置く。
本項では、無差別は凸で微分可能であると仮定し、まずは内点解にのみ焦点を当てる。本項の後半では仮定を緩めていく。
市場均衡
[編集]
ここでの目的は、初期賦存量からスタートして、追加的取引がもう発生しないような市場均衡が達成される価格を見つけることである。市場均衡における配分は、図2に描かれているように、2人の消費者の無差別曲線によって決まる。オクタビオとアビーは初期賦存量(ωx,ωy )と(Ωx – ωx , Ωy – ωy )(図2のω)を基に市場取引を行うと仮定する。2人の消費者は競争市場で交換を行う[注 1]。
財X2つが財Y1つと交換されるのであれば、オクタビオとアビーの取引は太字灰色の予算制約線上を動くことになる[注 2]。その他の価格水準の下での予算制約線も灰色の破線で描かれている。
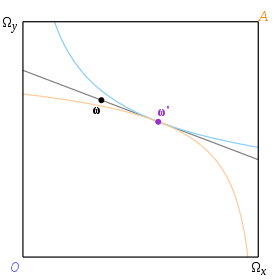
初期賦存量ωに対応する均衡点は、2人の消費者の無差別曲線の接点で決まり、その接線は点ωを通らなければならない。2つの無差別曲線に接する接線を「価格線」と呼ぶことにする。均衡点は予算制約線上にあり、価格線上にある。図3の点ω'が均衡配分である。その理由は以下のように説明できる。

ボックス内の点はどれも、オクタビオのいずれかの無差別曲線上にあり、アビーのいずれかの無差別曲線上にある。もし、図4が示すように無差別曲線が交差しているのであれば、無差別曲線を用いて4つの領域に分けることができる。淡い緑色で図示された領域は、両方の消費者にとって効用水準を上昇させる領域である。無差別曲線が交差する場合は、必ずこのような領域が現れるので、無差別曲線が交差する場合、その交点は均衡点とはなり得ない。
消費者が2人のみの経済では、取引がすべて同じ価格で行われるとは限らない、しかし、エッジワース・ボックス・ダイアグラムの目的は、競争がないときに価格調整が行われ得ることを示すことではなく、競争均衡を最小限の情報で図示することである。多くの消費者が存在する完全競争市場の経済では、全ての消費者が同じ価格に直面する。したがって、エッジワース・ボックス・ダイアグラムが示すような取引が行われる[9]。
厚生経済学の第一定理
[編集]2本の無差別曲線が接する点はパレート最適であることを確認した。同時に、2本の無差別曲線が共通の価格線の下で接する点は競争均衡(英:The competitive equilibrium)である。したがって、競争均衡はパレート最適である。この議論は、無差別曲線が微分可能でなく、競争均衡点がボックスの淵にある場合でも成り立つ。均衡の定義は、「追加的な取引がもう起こらない」である。そして、追加的な取引が起こらないということは、1人の消費者の効用水準を下げずにもう1人の消費者の効用水準を上昇させることはできないということである。これは、パレート最適の定義に等しい[13]。
均衡は「局所的に」パレート改善ができないことを意味する。つまり、局所的にパレート最適であることを意味する。しかし、パレート最適の定義はグローバルに見て(全体的に見て)パレート改善ができないことを要求する[注 3]。厚生経済学の第一定理には、完全競争の仮定は必要ない。消費者がお互いに同意するまで交換をし続ける限り、(少なくとも局所的には)パレート最適になる[14]。
厚生経済学の第二定理
[編集]
図7に示されるように、初期の配分がωである経済を考える。そして、ボックス内の他の点、例えばα'が社会的に好ましい点であるとする。この社会的に好ましい点がパレート最適であるとする。破線の予算制約線が実質所得の異なった配分に対応し、予算制約線上の動きは資源の再配分であり所得水準が固定されているものとする。
社会的に好ましい配分α'に行くには、オクタビオに(α'x,α'y)だけ保有させて残りをアビーに与えるような所得再分配をすればいい。しかし、実は、α'に行くにはα'を通過する価格線上のいずれかの点(例えばα)に資源を再配分してやれば十分である。そうすることで、自然に市場メカニズムに従って最適な配分α'に辿り着くことができる。
パレート集合
[編集]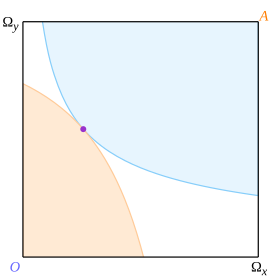
ある配分が、1人の消費者の効用水準を改善してもう1人の消費者の効用水準を低下させないとき、パレート支配的(英:Pareto dominate)であるという。パレート支配的な配分が他に存在しないとき、その配分はパレート最適(あるいはパレート効率的)であると言う。パレート最適な配分は「パレート集合(英:Pareto set)」または「効率曲線(英:Efficient locus)」と呼ばれる。
2つの無差別曲線に接する点(図5の紫の点)を考える。無差別曲線が凸であるので、接点以外に交差する点が存在しない。2つの無差別曲線によってボックスは3つの領域に分割される。淡い青の領域は、オクタビオの効用水準が上昇する領域で、アビーの効用水準が低下する領域である。淡いオレンジの領域は、アビーの効用水準が上昇する領域で、オクタビオの効用水準が低下する領域である。そして白の領域は、両者の効用水準が低下する領域である。つまり、2つの無差別曲線の接点がパレート最適であることにある。

パレート集合は、2つの無差別曲線の接点の集合であり、オクタビオの原点Oとアビーの原点Aを結ぶ。図6の紫の線がパレート集合である。パレート集合全体のことを契約曲線と呼ばれることがある。一方で、マスコレルらは、初期配分からスタートして、2人の消費者の効用水準が上昇するようなパレート集合を契約曲線と呼んでいる[15]。マスコレルらの定義の契約曲線は、コア(英:Core)とも呼ばれる[16] 。また、パレート集合は2人の無差別曲線が接する点の集合であるから、2人の消費者の限界代替率が等しい点でもある[注 4]。
オファー曲線
[編集]概念
[編集]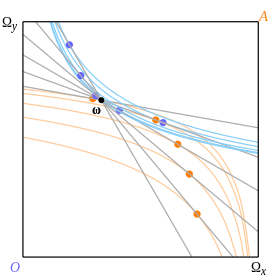
オファー曲線(英:Offer curves)は、均衡点を見つけるのに利用することができ、均衡の存在と一意性を検証するのに使うこともできる。初期配分を基に、それぞれの消費者のそれぞれの予算制約線の下で効用を最大化するような点(英:The preferred allocation)を見つけることができる。図8の青の点がオクタビオにとって最適な消費点であり、オレンジの点がアビーにとって最適な消費点である。当然のことながら、これらの点はそれぞれの消費者の無差別曲線に接している。

これらの最適消費点を結んだものがオファー曲線である。図9の濃い青の線がオクタビオのオファー曲線で、濃いオレンジの線がアビーのオファー曲線である。2人のオファー曲線はω'で交差しており、予算制約線もこの点を通過している。ω'に接する2人の無差別曲線がそれぞれ淡い色で描かれている。オファー曲線は必ず初期賦存点ωを通る。初期賦存点ω以外の2人のオファー曲線の交点は、均衡点となる。もちろん、初期賦存点ωにおいて2人の無差別曲線が接しているのであれば、そこは均衡点である[注 5]。
用語
[編集]オファー曲線の概念はヴィルフレド・パレートによって初めて提示された[9]。ただし、彼は「オファー曲線」ではなく「交換曲線(英:Exchange curves)」と呼んでいた。個々の予算制約上の最適消費点は「より好まれる配分(英:The preferred allocation)」と呼ばれ、これは現代的にはオクタビオの需要と解釈できる。「配分」はアビーとオクタビオの消費量の両方を決定するので、需要と供給の概念に近い。「オファー(Offre)」はフランス語で「供給」の意味であり、需要と供給を一致させるような点の集合と解釈できる。
注釈
[編集]脚注
[編集]出典
[編集]- ^ a b Schotter, Andrew (2008). Microeconomics: A Modern Approach. Cengage Learning.
- ^ a b Barbé, Lluís (2010). Francis Ysidro Edgeworth: A Portrait with Family and Friends. Edward Elgar Publishing.
- ^ Humphrey, Thomas M. (1996). “Early History of the Box Diagram”. Economic Quarterly 30 October 2016閲覧。.
- ^ Creedy, John (2008). "Francis Ysidro Edgeworth (1845–1926)", The New Palgrave Dictionary of Economics, 2nd Edition. Abstract.
- ^ Nash, John Forbes Jr. (1950). "The Bargaining Problem," Econometrica, 18(2), pp. 155-162.
- ^ Serrano, Roberto (2008). "Bargaining." The New Palgrave Dictionary of Economics, 2nd Edition. Abstract.
- ^ Pareto, Vilfredo (1906). Manual of Political Economy, New York, A.M. Kelley.
- ^ Walras, Leon (1874) Éléments d'Économie Politique Pure, ou Théorie de la Richesse Sociale.
- ^ a b c d Pareto, Vilfredo (1906). Manuale/Manuel.
- ^ Wald, Abraham (1936). Über einige Gleichungssysteme der mathematischen Ökonomie tr. as (1951). "On some Systems of Equations of Mathematical Economics".
- ^ Samuelson, Paul (1947). Foundations of Economic Analysi.
- ^ Arrow, Kenneth; Debreu, Gerard (1954). Existence of an Equilibrium for a Competitive Economy.
- ^ Wicksell, Knut (1906). Lectures on Political Economy.
- ^ Samuelson, Paul (1947). Foundations of Economic Analysis. p.204.
- ^ a b c Mas-Colell, Andreu; Whinston, Michael Dennis; Green, Jerry R. (1995). Microeconomic Theory, Oxford University Press.
- ^ Osborne, Martin J.; Rubinstein, Ariel (1994). A Course in Game Theory. Cambridge: MIT Press. ISBN 0-262-65040-1
