コンテンツにスキップ

クリフォード代数

出典: フリー百科事典『ウィキペディア（Wikipedia）』

数学において、クリフォード代数 (クリフォードだいすう、英: Clifford algebra) は結合多元環の一種である。K-代数として、それらは実数、複素数、四元数、そしていくつかの他の超複素数系を一般化する[1][2]。クリフォード代数の理論は二次形式と直交変換の理論と密接な関係がある。クリフォード代数は幾何学、理論物理学、デジタル画像処理を含む種々の分野において重要な応用を持つ。イギリス人幾何学者ウィリアム・キングドン・クリフォードにちなんだ名称である。

最もよく知られたクリフォード代数、あるいは直交クリフォード代数 (ちょっこうクリフォードだいすう、英: orthogonal Clifford algebra) は、リーマンクリフォード代数 (リーマンクリフォードだいすう、英: Riemannian Clifford algebra) とも呼ばれる[3]:83。

概要と動機

[編集]

通常のベクトル解析では、ベクトルの積として「内積（スカラーとなる）」と「外積（ベクトルとなる、ただし3次元のみ）」という異なる種類の演算を使い分ける必要がある。クリフォード代数（幾何代数とも呼ばれる）は、これらを単一の「幾何学的積（クリフォード積）」として統合し、より見通しの良い記述を可能にする数学的枠組みである。

幾何学的解釈

[編集]

実クリフォード代数は、幾何代数 (Geometric Algebra) としても知られ、幾何学的な操作を代数的に記述する枠組みを提供する。 この体系において、ベクトル の積（幾何学的積、あるいはクリフォード積） は、対称成分である内積 と、反対称成分である外積（ウェッジ積） の和として分解される。

ここで、内積 はスカラー（0-ベクトル）であり、外積 は2-ベクトル（bivector、向きを持った面要素）である。このように異なる次数の元（grade）の和を許容することで、回転や反射などの幾何学的変換を、行列を用いずに単一の代数系の中で記述できることが特徴である。

例えば、2次元ユークリッド空間の正規直交基底を （）とするとき、ベクトル と の積は以下のように計算される。

この演算結果において、定数項 は内積 に対応し、 の係数 は外積 の成分に対応する。項 は を満たすため、平面上の回転を生成する虚数単位としての役割を果たす。

具体的な構成

[編集]

V の次元を n とし、直交基底を {e1, …, en} とする。このとき、クリフォード代数 Cℓ(V, Q) は、以下の基底を持つ 2n 次元の多元環となる。

これらの基底の積は、前述の反可換関係 と、二乗の規則 を用いて計算できる。 これは、複素数や四元数の自然な一般化となっている（後述）。

外積代数の量子化として

[編集]

クリフォード代数は外積代数と近い関係にある。実際、二次形式が恒等的に 0（Q = 0）であれば、クリフォード関係式は となり、クリフォード代数 Cℓ(V, Q) は外積代数 ⋀(V) と一致する。 Q が 0 でない場合でも、基礎体 K の標数が 2 でなければ、Cℓ(V, Q) と ⋀(V) の間にはベクトル空間としての自然な同型（線型同型）が存在する。 すなわち、これらは「ベクトル空間としては同じ構造（同じ次元と基底）を持つ」が、「積の定義構造が異なる」代数系であるとみなせる。（標数 2 の場合にはそれらはなおベクトル空間として同型であるが、自然にではない）。指定された部分空間とクリフォード乗法を合わせた構造は、外積代数に比べてより豊かである。これは Q がもたらす追加の情報を用いているためである。

より正確には、ワイル代数が対称代数の量子化であるのと同じ方法で、クリフォード代数は外積代数の量子化（cf. 量子群）であると考えることができる。

ワイル代数とクリフォード代数ではさらに *-環という構造を持ち、CCR and CAR algebras において議論されているように、超代数（英語版）の偶項と奇項として統一できる。

基底と次元

[編集]

ベクトル空間V の体 K 上の次元が n であり {e1, …, en} が (V, Q) の直交基底（英語版）であれば、 クリフォード代数 Cℓ(V, Q) は K 上自由でその基底（の 1 つ）は以下で与えられる。

.

空積 (k = 0) は代数の乗法の単位元として定義される。k の各値に対して 個の基底元が存在する、したがってクリフォード代数の総次元は

V は二次形式を伴っているので、V の 特別な基底として直交基底を選べる。直交基底（英語版） は

for , and

であるような基底である。ただし ⟨-, -⟩ は Q に伴う対称双線型形式である。基本クリフォード関係式とはこの直交基底に対する積が

であることを意味している。このことにより直交基底ベクトルの扱いは極めて簡単になる。V の相異なる直交基底ベクトルの積 が与えられたとき、基底の添字が標準の順序になるように並べ替えたものは、必要な二元ごとの入れ替えの回数により決まる符号（すなわち整列させるための置換の符号）を付与することで得られる。

普遍性による定義

[編集]

数学的により厳密な定義は、圏論における普遍性を用いて行われる。この定義により、クリフォード代数が同型を除いて一意に定まることが保証される。

V を体 K 上のベクトル空間、Q: V → K をその上の二次形式とする。 クリフォード代数 Cℓ(V, Q) とは、K 上の単位的結合代数であり、以下の性質を満たす線型写像 i : V → Cℓ(V, Q) を備えたものである。

関係式の保持
任意の v ∈ V に対して、i(v)2 = Q(v)1 が成り立つ。
普遍性
A を K 上の任意の単位的結合代数とし、線型写像 j : V → A が任意の v ∈ V に対して j(v)2 = Q(v)1A を満たすとする。このとき、次の図式を可換にする代数準同型 f : Cℓ(V, Q) → A が一意的に存在する。

すなわち、クリフォード代数は、v2=Q(v) という関係式を満たす代数の中で「最も一般的」なものである。この普遍性により、同型を除いて一意に定まることが保証される。

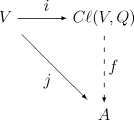
（標数が 2 でない場合）Q の代わりに対称双線型形式 ⟨·,·⟩ で考えると、線形写像 j に対する要求は次のようになる。

上で記述された普遍性をもつクリフォード代数は常に存在し、次のように構成できる。 V を含む最も一般的な代数であるテンソル代数 T(V) をとり、基本関係式が成り立つように適切な商をとるのである。具体的には、

の形のすべての元によって生成された T(V) の両側イデアル IQ を取り除くために、Cℓ(V, Q) を商代数

Cℓ(V, Q) ≔ T(V) / IQ

として定義する。この商によって継承される環の積はときどきクリフォード積 (Clifford product) と呼ばれ[4] 外積やスカラー積などとは別のものとして区別される。

すると Cℓ(V, Q) は V を含み、かつ上の普遍性を満たすことが直ちに示せる。この普遍性により Cℓ は同型を除いて一意に定まる。したがって、"その (the)" クリフォード代数 Cℓ(V, Q) と呼ぶことができる。この構成から i が単射であることも従う。通常は V を Cℓ(V, Q) の部分線型空間と同一視し、埋め込み i を省略して書く。

上記のようなクリフォード代数の普遍的な特徴づけは Cℓ(V, Q) の構成が事実上関手的であることを示している。すなわち、Cℓ は二次形式を持ったベクトル空間の圏（射は二次形式を保つ線型写像）から結合代数への関手と考えることができる。普遍性は（二次形式を保つ）ベクトル空間の間の線型写像を結合クリフォード代数の間の代数準同型（英語版）として一意に拡張できることを保証する。

例： 実および複素のクリフォード代数

[編集]

最も重要なクリフォード代数は非退化2次形式を備えた実および複素ベクトル空間上のものである。

代数 Cℓp,q(R) と Cℓn(C) の各々は A あるいは A ⊕ A に同型である、ただし A は成分が R, C あるいは H から来る全行列環、ということが明らかになる。これらの代数の完全な分類はクリフォード代数の分類（英語版）を見よ。

実係数の場合

[編集]
→詳細は「幾何代数（英語版）」を参照

実クリフォード代数の幾何学的な解釈は幾何代数（英語版）として知られている。

有限次元実ベクトル空間上のすべての非退化2次形式は標準対角形式

に同値である、ただし n = p + q はベクトル空間の次元である。整数の組 (p, q) は二次形式の符号数と呼ばれる。この二次形式を持った実ベクトル空間はしばしば Rp,q と表記される。Rp,q 上のクリフォード代数は Cℓp,q(R) と表記される。記号 Cℓn(R) は著者が正定値と不定値の空間どちらを好むかによって Cℓn,0(R) あるいは Cℓ0,n(R) を意味する。

Rp,q の標準正規直交基底 (ei) は互いに直交する n = p + q 個のベクトルからなり、そのうち p 個はノルム +1 を持ち、q 個はノルム −1 を持つ。代数 Cℓp,q(R) は従って平方して +1 になる p 個のベクトルと平方して −1 になる q 個のベクトルを持つ。

Cℓ0,0(R) は自然に R に同型であることに注意する。0 でないベクトルはないからである。Cℓ0,1(R) は平方して −1 になるただ 1 つのベクトル e1 によって生成される 2 次元の代数なので複素数体 C に同型である。代数 Cℓ0,2(R) は {1, e1, e2, e1e2} によって張られる 4 次元の代数である。後ろ 3 つの元は平方して −1 になりすべて反交換するので、代数は四元数体 H に同型である。Cℓ0,3(R) は 分解型双四元数（英語版）と呼ばれる直和 H ⊕ H に同型な 8 次元の代数である。

複素係数の場合

[編集]

複素ベクトル空間上でもクリフォード代数を考えることができる。複素ベクトル空間上のすべての非退化二次形式は標準対角形式

（ただし n = \dim V）に同型を除いて同値である。したがって各次元 n に対してただ1つの非退化なクリフォード代数が存在する。標準二次形式を持った Cn 上のクリフォード代数は Cℓn(C) と表記される。

低次元における例は以下の通りである。

Cℓ0(C) ≅ C: 複素数体
Cℓ1(C) ≅ C ⊕ C: 双複素数環
Cℓ2(C) ≅ M(2, C): 双四元数（英語版）環

ここで、M(n, C) は C 上の n×n 行列環を表す。

例：四元数と双対四元数の構成

[編集]

四元数

[編集]

ハミルトンの四元数 H は、クリフォード代数としていくつかの方法で構成できるが、代表的なものは Cℓ0,2(R) そのもの、あるいは Cℓ0,3(R) の偶部分代数 Cℓ00,3(R) と見る方法である。

ここでは Cℓ0,3(R) の偶部分代数としての構成を示す。 実 3 次元空間 R3 を考え、その基底 e1, e2, e3 に対して、負定値の計量 Q(ei) = -1 を導入する[注釈 1]。 クリフォード代数の関係式は以下のようになる：

このとき、Cℓ0,3(R) の元の中で、2つの基底の積（2-ベクトル）として定義される以下の要素を考える：

これらは以下の性質を満たすことが確認できる。ここで、異なる基底同士は反可換（）であり、 であることに注意する。

同様に jk = i, ki = j も成り立ち、これらは四元数の虚数単位 i, j, k の満たす関係式と一致する。したがって、1, i, j, k で張られる部分空間（偶部分代数）は四元数体 H と同型である。

この対応関係は、四元数が単なる抽象的な代数ではなく、3次元空間の幾何学（特に回転）と密接に結びついていることを示している。

  • は、軸と軸で張られる平面（平面）を表す2-ベクトル（bivector）である。
  • この平面を表す をベクトルに掛けることは、その平面内での90度回転に対応する。

このように、クリフォード代数の視点導入することで、四元数 を「虚数」という不思議な数としてではなく、「回転の基準となる平面」という幾何学的な実体として理解できる。

なお、四元数をさらに拡張した八元数（オクトニオン）も存在するが、八元数は乗法の結合法則を満たさない（ となる場合がある）ため、結合多元環であるクリフォード代数の枠組みには直接的には含まれない。しかし、クリフォード代数と同様にケーリー＝ディクソンの構成法によって体系づけられる関係にあり、高次元の物理現象の記述などで比較・研究されることがある。

R3 の直交単位ベクトルの集合を e1, e2, e3 として表記すると、クリフォード積は関係

および

を生み出す。クリフォード代数 Cℓ0,3(R) の一般の元は

によって与えられる。

Cℓ0,3(R) の偶次数元の線型結合は一般元

とともに Cℓ 0
0,3 (R) の偶部分代数を定義する。基底元は四元数基底元 i, j, k と

として同一視することができ、これは偶部分代数 Cℓ 0
0,3 (R) はハミルトンの実四元数代数であることを示している。

双対四元数

[編集]

このセクションにおいて、双対四元数が退化二次形式を持った実四次元空間の偶クリフォード代数として構成される[5][6]。

ベクトル空間 V を実四次元空間 R4 とし、その基底を とする。ここで、 が張る部分空間上では標準的なユークリッド計量と一致し、 に対しては かつ他の基底と直交するような退化二次形式 Q を導入する。 すなわち、任意のベクトル に対して、以下の退化双線型形式を考える。

この形式において、第4成分は計量に寄与しない（等方的な）次元となる。

ベクトル v と w のクリフォード積は

によって与えられる。負号は四元数との対応を簡単にするために導入していることに注意しよう。

R4 の直交単位ベクトルの集合を e1, e2, e3, e4 として表記すると、クリフォード積は関係

と

を生み出す。

クリフォード代数 Cℓ(R4,d) の一般元は 16 個の成分を持つ。偶次数付けられた元の線型結合は次の形の一般元を持った偶部分代数 Cℓ0(R4,d) を定義する

基底元は四元数基底元 i, j, k と双対単位 ε と

として同一視できる。これは Cℓ 0
0,3,1 (R) の双対四元数代数との対応を提供する。

これを見るには、次式を計算する

と

e1 と e4 の交換は偶数回符号を交代し、双対単位 ε が四元数基底元 i, j, k と交換することを示す。

性質

[編集]

外積代数との関係

[編集]

ベクトル空間 V が与えられると外積代数 ⋀(V) は V 上の二次形式に依存せず構成でき、その次元は 2^{\dim V} である。K の標数が 2 でなければ、⋀(V) と Cℓ(V, Q) の間には、ベクトル空間としての自然な同型（線型同型）が存在する。これが代数同型であることと Q = 0 は同値である。したがってクリフォード代数 Cℓ(V, Q) を Q に依存した積で V 上の外積代数を豊かにしたもの（あるいはより正確には、量子化、 cf. 導入）と考えることができる（外積はなお Q とは独立に定義できる）。

同型を確立する最も易しい方法は V の直交基底 {ei} をとりそれを上で述べられたように Cℓ(V, Q) の基底に拡張することである。写像 Cℓ(V, Q) → ⋀(V) は

によって決定される。これは基底 {ei} が直交しているときにのみうまくいくことに注意しよう。この写像は直交基底の選択とは独立であり従って自然同型を与えることを示すことができる。

K の標数が 0 であれば、反対称化によっても同型を確立できる。関数 fk: V × ⋯ × V → Cℓ(V, Q) を

によって定義する、ただし和は k 個の元の上の置換群を渡って取られる。fk は交代形式（英語版）なのでそれは一意的な線型写像 ⋀k(V) → Cℓ(V, Q) を誘導する。これらの写像の直和は ⋀(V) と Cℓ(V, Q) の間の線型写像を与える。この写像は線型同型であることを示すことができ、それは自然である。

関係を見るより洗練された方法は Cℓ(V, Q) 上フィルトレーション（英語版）を構成することである。テンソル代数 T(V) は自然なフィルトレーションを持つことを思い出そう： F0 ⊂ F1 ⊂ F2 ⊂ ⋯、ただし Fk は k-階以下のテンソルの和を含む。これをクリフォード代数に射影することで Cℓ(V, Q) 上のフィルトレーションが得られる。伴う次数代数

は自然に外積代数 ⋀(V) に同型である。フィルター代数の伴う次数代数は（すべての k に対してFk のコンポーネントを Fk+1 の中に選ぶことによって）つねにフィルターベクトル空間としてフィルター代数に同型であるから、これは任意の標数において、2 でさえも、（自然なものではないが）同型を提供する。

次数付け

[編集]

以降では標数は 2 でないとする[注釈 2]。

クリフォード代数は Z2-次数代数（超代数（英語版）としても知られている）である。実際、v ↦ −v によって定義される V 上の線型写像（原点を通る反射（英語版））は二次形式 Q を保存ししたがってクリフォード代数の普遍性によって代数自己同型

α: Cℓ(V, Q) → Cℓ(V, Q)

に拡張する。α は対合（すなわち自乗すると恒等関数になる）であるから、Cℓ(V, Q) を α の正と負の固有空間に分解できる

ただし Cℓi(V, Q) ≔ {x ∈ Cℓ(V, Q)  |  α(x) = (−1)ix}。α は自己同型であるから

が従う、ただし右上の添え字は modulo 2 で読まれる。これは Cℓ(V, Q) に Z2-次数代数の構造を与える。部分空間 Cℓ0(V, Q) は Cℓ(V, Q) の部分代数をなし、偶部分代数 (even subalgebra) と呼ばれる。部分空間 Cℓ1(V, Q) は Cℓ(V, Q) の奇成分 (odd part) と呼ばれる（部分代数ではない）。この Z2-次数付けはクリフォード代数の解析と応用において重要な役割を果たす。自己同型 α は主対合 (main involution) あるいは次数付き対合 (grade involution) と呼ばれる。この Z2-次数付けにおいて pure な元は単に even あるいは odd と呼ばれる。

注意
標数が 2 でなければ Cℓ(V, Q) の基礎ベクトル空間は N-次数付けと Z-次数付けを外積代数 ⋀(V) の基礎ベクトル空間との自然な同型から受け継ぐ[注釈 3]。しかしながら、これはベクトル空間の次数付けでしかないことに注意することは重要である。つまり、クリフォード乗法は N-次数付けや Z-次数付けをリスペクトせず、Z2-次数付けだけなのである： 例えば Q(v) ≠ 0 であれば v ∈ Cℓ1(V, Q) だが v2 ∈ Cℓ0(V, Q) であって Cℓ2(V, Q) に入らない。幸運なことに、次数付けは自然な方法で関係している： Z2 ≅N/2N≅ Z/2Z。さらに、クリフォード代数は Z-filtered（英語版）である： Cℓ≤i(V, Q) ⋅ Cℓ≤j(V, Q) ⊂ Cℓ≤i+j(V, Q)。クリフォード数の次数 (degree) は通常 N-次数付けにおける次数のことである。

クリフォード代数の偶部分代数 Cℓ0(V, Q) は、それ自身があるクリフォード代数に同型となる場合がある[注釈 4][注釈 5]V がノルム Q(a) の部分空間 U のベクトル a の直交直和であれば、Cℓ0(V, Q) は Cℓ(U, −Q(a)Q) に同型である、ただし −Q(a)Q は U に制限され −Q(a) を掛けた形式 Q である。特に実数体上これは次を意味する

負定値の場合にはこれは包含 Cℓ0,n−1(R) ⊂ Cℓ0,n(R) を与え、列を拡張する

R ⊂ C ⊂ H ⊂ H ⊕ H ⊂ ⋯;

同様に、複素の場合には、Cℓn(C) の偶部分代数は Cℓn−1(C) に同型であることを示せる。

反自己同型写像

[編集]

自己同型 α に加えて、クリフォード代数の解析において重要な役割を果たす 2 つの反自己同型（英語版）が存在する。テンソル代数 T(V) はすべての積の順序を逆にする反自己同型とともに来ることを思い出そう：

イデアル IQ はこの反転の下で不変なので、この演算は Cℓ(V, Q) の反自己同型に降り、転置 (transpose) あるいは反転 (reversal) 演算と呼ばれ、tx によって表記される。この反転は反自己同型である： t(xy) = ty tx。転置演算は Z2-次数付けを全く使わないので2つ目の反自己同型を α と転置を合成することによって定義する。この演算をクリフォード共役 (Clifford conjugation) と呼び x と表記する

2 つの反自己同型のうち転置はより基本的である[注釈 6]。

これらの演算は全て対合であることに注意しよう。それらは Z-次数付けにおいて pure な元上 ±1 として作用することを示すことができる。実際、すべての 3 つの演算は次数 modulo 4 にしか依らない。つまり、x が pure で次数 k であれば、

ただし符号は以下の表によって与えられる：

k mod 40123
+−+−(−1)k
++−−(−1)k(k−1)/2
+−−+(−1)k(k+1)/2

クリフォードスカラー積

[編集]

標数が 2 でないとき、V 上の二次形式 Q は Cℓ(V, Q) のすべての上の二次形式に拡張することができる（これも Q によって表記する）。1 つのそのような拡張の基底に依存しない定義は

ただし は a のスカラー部分（Z-次数付けにおいて次数 0 の部分）を表記する。

を示すことができる、ただし vi は V の元である – この恒等式は Cℓ(V, Q) の任意の元に対しては正しく「ない」。

Cℓ(V, Q) 上の伴う対称双線型形式は

によって与えられる。これは V に制限されたときにもとの双線型形式に戻ることを確認できる。 Cℓ(V, Q) のすべての上の双線型形式が非退化であることとそれが V 上非退化であることは同値である。

転置はこの内積に関して左/右クリフォード乗法の随伴であることを証明するのは難しくない。つまり、

および

クリフォード代数の構造

[編集]

この節ではベクトル空間 V の次元は有限であり Q の双線型形式は非特異であると仮定する。K 上の中心単純代数は中心が K の（有限次元）可除代数上の行列代数である。例えば、実数体上の中心単純代数は実数体あるいは四元数体上の行列代数である。

  • V の次元が偶数であれば Cℓ(V, Q) は K 上の中心単純代数である。
  • V の次元が偶数であれば Cℓ0(V, Q) は K の二次拡大上の中心単純代数であるかまたは K 上の 2 つの同型な中心単純代数の和である。
  • V の次元が奇数であれば Cℓ(V, Q) は K の二次拡大上の中心単純代数であるかまたは K 上の 2 つの同型な中心単純代数の和である。
  • V の次元が奇数であれば Cℓ0(V, Q) は K 上の中心単純代数である。

以下の結果を用いるとクリフォード代数の構造は明示的に解明される。U の次元は偶数で判別式 d の非特異双線型形式を持っているとし、V は二次形式を持つ別の空間とする。U + V のクリフォード代数は U と (−1)dim(U)/2dV のクリフォード代数のテンソル積に同型であり、後者はその二次形式に (−1)dim(U)/2d を掛けた空間 V である。これは実数体上では特に次のことを意味する

これらの公式を用いることで実と複素のすべてのクリフォード代数の構造が導かれる。クリフォード代数の分類（英語版）を見よ。

とりわけ、クリフォード代数の森田同値類（その表現論： それ上の加群の圏の同値類）は符号 (p − q) mod 8 のみに依っている。これはボットの周期性（英語版）の代数的な形である。

クリフォード群

[編集]

クリフォード群のクラスはルドルフ・リプシッツ (Rudolf Lipschitz) によって発見された[7]。

このセクションにおいて V は有限次元で二次形式 Q は非退化であると仮定する。

クリフォード代数の元へのその可逆元の群による作用は、「捻られた共役 (twisted conjugation)」を用いて定義できる。これは、写像 y ↦ xyα(x)−1 （ただし α は上で定義された主対合）による作用である。

クリフォード群 Γ は、この作用の下でベクトル空間 V を不変にする (stabilize vectors) 可逆元 x の集合として定義される。これが意味するのは V のすべての v に対して：

この公式はまたノルム Q を保つベクトル空間 V 上のクリフォード群の作用を定義し、従ってクリフォード群から直交群への準同型を与える。クリフォード群はノルムが 0 でない V のすべての元 r を含み、これらは v に対する超平面での鏡映 (reflection) として V 上に作用する：

（標数 2 の場合、この操作は「直交トランスベクション (orthogonal transvection)」と呼ばれる。）

クリフォード群 Γ は2 つの部分集合 Γ0 と Γ1 の非交和である、ただし Γi は次数 i の元の部分集合である。部分集合 Γ0 は Γ において指数 2 の部分群である。

V が正定値（あるいは負定値）二次形式を持った有限次元実ベクトル空間であればクリフォード群は（カルタン・デュドネの定理によって）その形式に関して V の直交群に全射し核は体 K の 0 でない元からなる。これは次の完全列を導く

他の体上あるいは不定値形式では、写像は一般には全射ではなく、失敗はスピノルノルムによってとらえられる。

スピノルノルム

[編集]
→詳細は「en:Spinor_norm § Galois_cohomology_and_orthogonal_groups」を参照

任意の標数において、スピノルノルム Q はクリフォード群上

によって定義される。それはクリフォード群から K の非零元の群 K* への準同型である。それは V をクリフォード代数の部分空間と同一視したときに V の二次形式 Q と一致する。著者によってはスピノルノルムの定義が僅かに異なり、ここでのものとは Γ1 上 −1, 2, あるいは −2 の因子によって異なる。違いは標数が 2 でなければそれほど重要ではない。

K の 0 でない元は体 K の非零元の平方の群 K*2 にスピノルノルムを持つ。なので V が有限次元で非特異なとき V の直交群から群 K*/K*2 への誘導写像を得、これもまたスピノルノルムと呼ばれる。ベクトル r の鏡映のスピノルノルムは K*/K*2 において像 Q(r) を持ち、この性質は直交群上それを一意的に定義する。これは次の完全列を与える：

標数 2 においては群 {±1} はただ 1 つの元を持つことに注意せよ。

代数群のガロワコホモロジーの視点から、スピノルノルムはコホモロジーの連結準同型である。1 の平方根の代数群（標数が 2 でない体上それは大雑把には自明なガロワ作用を持った 2 元群と同じである）を μ2 と書くと、短完全列

はコホモロジーの長完全列を生み出し、それは

で始まる。K に係数を持つ代数群の 0 次ガロワコホモロジー群は単に K-値点の群である： H0(G; K) = G(K)、および H1(μ2; K) ≅ K*/K*2, よって前の列を復元する：

ただしスピノルノルムは連結準同型 H0(OV; K) → H1(μ2; K) である。

スピン群とピン群

[編集]
→詳細は「スピン群」、「ピン群」、および「スピノル」を参照

本節において V は有限次元でありその双線型形式は非特異であると仮定する。（K が標数 2 であればこれは V の次元が偶数であることを含む。）

ピン群 PinV(K) はスピノルノルム ±1 の元のクリフォード群 Γ の部分群であり、同様にスピン群 SpinV(K) は PinV(K) においてディクソン不変量 0 の元の部分群である。標数が 2 でないとき、これらは行列式 1 の元である。スピン群は通常ピン群において指数 2 を持つ。

クリフォード群から直交群への全射準同型が存在することを直前のセクションから思い出そう。特殊直交群を Γ0 の像として定義する。K の標数が 2 でなければこれは単に直交群の行列式 1 の元の群である。K の標数が 2 であれば、直交群のすべての元は行列式 1 をもち、特殊直交群はディクソン不変量 0 の元の集合である。

ピン群から直交群への準同型が存在する。像はスピノルノルム 1 ∈ K*/K*2 の元からなる。核は元 +1 と −1 からなり、K の標数が 2 でなければ位数 2 をもつ。同様にスピン群から V の特殊直交群への準同型が存在する。

V が実数上正あるいは負定値空間である共通の場合において、スピン群は特殊直交群の上へと写り V の次元が少なくとも 3 であれば単連結である。さらにこの準同型の核は 1 と −1 からなる。なのでこの場合スピン群 Spin(n) は SO(n) の二重被覆である。しかしながら、スピン群の単連結性は一般には正しくない。V がともに 2 以上の p, q に対して Rp,q であればスピン群は単連結ではないことに注意が必要である。この場合、代数群 Spinp,q は代数群として単連結であるが、その実数値点の群 Spinp,q(R) は単連結とは限らない。

スピノル

[編集]

クリフォード代数 Cℓp,q(C) で p + q = 2n と偶数になるものは 2n 次元の複素表現を持つ行列代数である。群 Pinp,q(R) に制限することにより同じ次元の Pin 群の複素表現を得、これはスピン表現（英語版）と呼ばれる。これをスピン群 Spinp,q(R) に制限すれば次元 2n−1 の 2 つの半スピン表現（あるいはワイル表現）の和として分解する。

p + q = 2n + 1 と奇数になればクリフォード代数 Cℓp,q(C) はそれぞれが 2n 次元の表現を持っているような 2 つの行列代数の和であり、これらもまた両方ともピン群 Pinp,q(R) の表現である。スピン群 Spinp,q(R) への制限上これらは同型になり、したがってスピン群は次元 2n の複素スピノル表現を持つ。

より一般に、任意の体上のスピノル群とピン群は正確な構造が対応するクリフォード代数の構造（英語版）に依存する同様の表現を持つ：クリフォード代数がある可除代数上の行列代数である因子を持つときにはいつでもその可除代数上のピンとスピン群の対応する表現を得る。例えば実数体上の場合についてはスピノールの記事を見よ。

実スピノル

[編集]
→詳細は「スピノール」を参照

実スピン表現を記述するために、スピン群がクリフォード代数の中にどのようにあるかを知らなければならない。ピン群 Pinp,q は単位ベクトルの積として書ける Cℓp,q の可逆元の集合である：

クリフォード代数の上の具体的な実現と比べて、ピン群は任意にたくさんの鏡映の積に対応する： それは全直交群 O(p, q) の被覆である。スピン群は単位ベクトルの偶数個の積であるような Pinp,q の元からなる。したがってカルタン・デュドネの定理によって Spin は固有回転の群 SO(p, q) の被覆である。

α: Cℓ → Cℓ を pure ベクトルに作用する写像 v ↦ −v によって与えられる自己同型とする。すると特に Spinp,q は元が α によって固定される Pinp,q の部分群である。

とする。（これらは Cℓp,q においてちょうど偶数次の元である。）するとスピン群は Cℓ 0
p,q  の中にある。

Cℓp,q の既約表現はピン群の表現を与えるために制限する。逆に、ピン群は単位ベクトルで生成されるから、その既約表現のすべてはこのようにして誘導される。したがって 2 つの表現は一致する。同じ理由のため、スピンの既約表現は Cℓ p,q
0  の既約表現と一致する。

ピン表現を分類するためには、クリフォード代数の分類（英語版）の結果を利用すればよい。（偶部分代数の表現である）スピン表現を見つけるためには、まず次の同型のいずれかを利用できる（上記参照）

Cℓ 0
p,q  ≈ Cℓp,q−1 (for q > 0);
Cℓ 0
p,q  ≈ Cℓq,p−1 (for p > 0).

そして符号 (p, q − 1) あるいは (q, p − 1) におけるピン表現として符号 (p, q) におけるスピン表現を実現できる。

応用

[編集]

微分幾何学

[編集]

外積代数の主要な応用の一つは微分幾何学にありそこではそれが滑らかな多様体上の微分形式のファイバー束を定義するために使われる。（擬）リーマン多様体の場合には、接空間は計量によって誘導される自然な二次形式を持つ。したがって、外束（英語版）とのアナロジーでクリフォード束（英語版）を定義できる。これはリーマン幾何学においてたくさんの重要な応用を持つ。おそらくより重要なのはスピン多様体、その付随するスピノル束（英語版）そして spinc 多様体へのつながりであろう。

物理学

[編集]

物理学、特に相対論的量子力学において、クリフォード代数は必須の言語となっている。ポール・ディラックは、電子の波動方程式（ディラック方程式）を導出する際、以下の反交換関係を満たす4つの係数 （ガンマ行列）を導入した。

ここで、 はミンコフスキー計量（符号 または ）、 は単位行列である。

この関係式は、まさにクリフォード代数の定義関係式 そのものである。 すなわち、ディラックが導入した「ガンマ行列」とは、時空に対応するベクトル空間上のクリフォード代数の生成元 の行列表現に他ならない。

  • *生成元:
  • 関係式:

この視点に立つと、電子のスピンなどの性質を持つ「スピノル」は、単なる列ベクトルではなく、クリフォード代数の左イデアル（あるいはその表現空間の元）として幾何学的に理解される。これにより、物理学者は抽象的な代数構造と具体的な行列計算を行き来することができる。

ディラック行列は、クリフォード代数 Cℓ1,3(R) （または符号によっては Cℓ3,1(R)）の複素化 Cℓ1,3(C) が、4次複素行列環 と同型であるという事実に基づいている。

ディラック行列は最初ポール・ディラックによって、電子に対する相対論の一階波動方程式を書き、クリフォード代数から複素行列への明示的な同型を与えようとしていた時に、書き下された。結果はディラック方程式を定義しディラック作用素を導入するために用いられた。クリフォード代数全体はディラック場双線型（英語版）の形式の場の量子論において現れる。

量子論を記述するためのクリフォード代数の使用は中でも Mario Schönberg[8]によって、geometric calculus の言葉では David Hestenes と Basil Hiley と hierarchy of Clifford algebras の共同研究者によって、そして Elio Conte et al.[9][10]によって進められてきた。

コンピュータグラフィックスと工学

[編集]

クリフォード代数（特に幾何代数と呼ばれる文脈）は、コンピュータグラフィックス、ロボット工学、コンピュータビジョンの分野で強力なツールとして利用されている。

回転と並進の統合
従来のベクトル解析では、回転は行列や四元数、並進はベクトル加算と別々に扱われていたが、クリフォード代数（特に双対四元数や共形幾何代数）を用いることで、これらを単一の演算として統一的に記述できる。これは、ロボットのアーム制御（キネマティクス）や3Dオブジェクトの補間（スキニング）計算において、計算コストの削減や特異点（ジンバルロック）の回避に寄与する。
プリミティブ図形の扱い
点、線、面、球などを代数の元として統一的に表現でき、それらの交差判定や射影といった操作を代数的な積として簡潔に記述できる。
高次元データ解析
色情報やオプティカルフローなどの多次元データをベクトル値として直接扱う信号処理（クリフォード・フーリエ変換（英語版）など）への応用も研究されている[11]。

関連項目

[編集]

脚注

[編集]

注釈

[編集]
  1. ↑ あるいは正定値計量を考え、関係式を と定義する流儀もあるが、結果として得られる代数構造は同じである。
  2. ↑ したがって群環 K[Z/2] は半単純でありクリフォード代数は主対合の固有空間に分解する。
  3. ↑ Z-次数付けは N 次数付けから負の整数で添え字づけられた零部分空間のコピーを追加することによって得られる。
  4. ↑ 技術的には、指定されたベクトル部分空間なしにはそれはクリフォード代数としての完全な構造を持たない。
  5. ↑ なお標数は 2 でないことを仮定している。
  6. ↑ 代わりに (−) の規約を用いるときは、逆に共役がより基本的となる。一般に、共役と転置の意味は一方の符号の規約からもう一方へと移るときに交換される。例えば、ここで使われる慣習ではベクトルの逆は v−1 = vt / Q(v) によって与えられ、一方 (−) 規約 では v−1 = v / Q(v) によって与えられる。

出典

[編集]
  1. ↑ Clifford, W. K. (1873), “Preliminary sketch of bi-quaternions”, Proc. London Math. Soc. 4: 381–395
  2. ↑ Clifford, W. K. (1882), Tucker, R., ed., Mathematical Papers, London: Macmillan
  3. ↑ 例えば Oziewicz, Z.; Sitarczyk, Sz. (1992), “Parallel treatment of Riemannian and symplectic Clifford algebras.”, in Micali, Artibano; Boudet, Roger; Helmstetter, Jacques, Clifford Algebras and their Applications in Mathematical Physics, Kluwer Academic Publishers, ISBN 0-7923-1623-1
  4. ↑ Lounesto 2001, §1.8.
  5. ↑ J. M. McCarthy, An Introduction to Theoretical Kinematics, pp. 62–5, MIT Press 1990.
  6. ↑ O. Bottema and B. Roth, Theoretical Kinematics, North Holland Publ. Co., 1979
  7. ↑ Lounesto 2001, §17.2.
  8. ↑ See the references to Schönberg's papers of 1956 and 1957 as described in section "The Grassmann–Schönberg algebra " of:A. O. Bolivar, Classical limit of fermions in phase space, J. Math. Phys. 42, 4020 (2001) doi:10.1063/1.1386411
  9. ↑ Conte, Elio (2002). “A Quantum Like Interpretation and Solution of Einstein, Podolsky, and Rosen Paradox in Quantum Mechanics”. pp. 271–304. arXiv:0711.2260 [quant-ph].
  10. ↑ Elio Conte: On some considerations of mathematical physics: May we identify Clifford algebra as a common algebraic structure for classical diffusion and Schrödinger equations? Adv. Studies Theor. Phys., vol. 6, no. 26 (2012), pp. 1289–1307
  11. ↑ Rodriguez, Mikel; Shah, M (2008). “Action MACH: A Spatio-Temporal Maximum Average Correlation Height Filter for Action Classification”. Computer Vision and Pattern Recognition (CVPR).

参考文献

[編集]

関連文献

[編集]

外部リンク

[編集]
「https://ja.wikipedia.org/w/index.php?title=クリフォード代数&oldid=107355858」から取得